DirichletDistribution
DirichletDistribution[{α1,…,αk+1}]
次元 k,形状母数 αiのディリクレ(Dirichlet)分布を表す.
詳細
- DirichletDistributionは多変量ベータ分布としても知られている.
- ディリクレ分布におけるベクトル
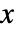 の確率密度は,
の確率密度は,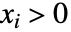 と
と では
では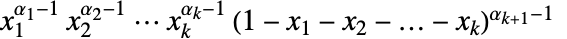 に比例する.
に比例する. - DirichletDistributionでは,αiは任意の正の実数でよい.
- DirichletDistributionでは,αiは無次元量でよい.
- DirichletDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- DirichletDistribution[{α1,…,αk+1}]は,和が1未満で
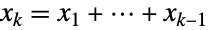 である正の実数の k タプル
である正の実数の k タプル 上で定義された多変量連続統計分布を表す.DirichletDistribution[{α1,…,αk+1}]の周辺分布(MarginalDistribution) は,成分 αiのさまざまな線形結合でパラメータ化されたあらゆる種類のBetaDistributionである.結果として,ディリクレ分布は,その成分 αiがすべて正の実数であり,その確率密度関数(PDF)の形を決定する,
上で定義された多変量連続統計分布を表す.DirichletDistribution[{α1,…,αk+1}]の周辺分布(MarginalDistribution) は,成分 αiのさまざまな線形結合でパラメータ化されたあらゆる種類のBetaDistributionである.結果として,ディリクレ分布は,その成分 αiがすべて正の実数であり,その確率密度関数(PDF)の形を決定する,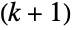 タプル(α1,…,αk+1)でパラメータ化される.ディリクレ分布は,多変量ベータ分布と呼ばれることがある.
タプル(α1,…,αk+1)でパラメータ化される.ディリクレ分布は,多変量ベータ分布と呼ばれることがある. - ディリクレ分布のPDFの絶対最大値は,その平均,つまり,成分がその一変量周辺分布のPDFの一変数平均である k ベクトルにある.ディリクレ分布に対応する,関連する各周辺分布のPDFの裾部は,周辺分布のPDFが大きい値の
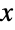 について指数的というよりも代数的に減少するという意味で「太い」(この動作は,これらの分布のSurvivalFunctionを分析することによって,定量的に厳密にすることができる).
について指数的というよりも代数的に減少するという意味で「太い」(この動作は,これらの分布のSurvivalFunctionを分析することによって,定量的に厳密にすることができる). - ディリクレ分布は,ドイツ人の数学者であるJohann Dirichletにちなんで命名された.この分布は,1970年代にThomas Fergusonによって正式に導入されて以来,現実世界と理論上の現象の両方をモデル化するためのツールとして使われてきた.ディリクレ分布は,より普遍的なディリクレ過程,簡単に言えば,特定のアルゴリズムに従ってある確率分布を確率分布の各集合に割り当てる無限次元確率過程,の有限バージョンである.同様に,ディリクレ分布は,MultinomialDistributionについての共役事前分布としてを含み,ベイズ統計の事前分布としてもしばしば現れる.ディリクレ分布の興味深い応用の一つに,長年に渡って製造される(公正な)サイコロについての,より最近製造されたサイコロの方が,製造過程の精度が上がったためにより「公正な」ことに注目した,確度のでたらめさのモデリングがある.ディリクレ分布は,データマイニング,機械学習,コンピュータビジョンにも応用されている.より最近では,ディリクレ分布はテキスト集合中の単語頻度のモデル化に使われている.
- RandomVariateを使って,ディリクレ分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[{x1,…,xk},DirichletDistribution[{α1,…,αk+1}]](より簡略すると {x1,…,xk}DirichletDistribution[{α1,…,αk+1}])を使って,確率変数の k タプル(x1,…,xk)が,ディリクレ分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[DirichletDistribution[{α1,…,αk+1}],{x1,…,xk}]およびCDF[DirichletDistribution[{α1,…,αk+1}],{x1,…,xk}]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.さらに,Covarianceを使ってDirichletDistributionに対応する共分散行列を計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がディリクレ分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックディリクレ分布を推定することが,FindDistributionParametersを使ってデータをディリクレ分布にフィットすることができる.ProbabilityPlotを使って記号ディリクレ分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ディリクレ分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたディリクレ分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってディリクレ分布を含む高次元分布を構築することが,ProductDistributionを使ってディリクレ分布を含む独立成分分布の結合分布を計算することができる.
- DirichletDistributionは,数多くの他の分布と関連している.先述の通り,DirichletDistributionは,両者それぞれの周辺分布がベータ分布であるという意味で,BetaDistributionと緊密な関係がある.さらに,任意の一次元ディリクレ分布は,DirichletDistribution[{α1,α2}]のPDFが厳密にBetaDistribution[α1,α2]のPDFであるという意味において,ベータ分布である.DirichletDistributionはまた,
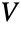 が k 個の独立分布に従うガンマ変量 Y1,…,Ykの和によって定義されるガンマ分布に従う確率変数である場合は常に,確率変数
が k 個の独立分布に従うガンマ変量 Y1,…,Ykの和によって定義されるガンマ分布に従う確率変数である場合は常に,確率変数 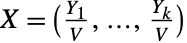 がDirichletDistributionに従って分布しているという意味で,GammaDistributionにも関連している.DirichletDistributionはMultinomialDistributionの事前共役分布であり,BetaPrimeDistribution,CompoundPoissonDistribution,MultinormalDistributionとも関係している.
がDirichletDistributionに従って分布しているという意味で,GammaDistributionにも関連している.DirichletDistributionはMultinomialDistributionの事前共役分布であり,BetaPrimeDistribution,CompoundPoissonDistribution,MultinormalDistributionとも関係している.
例題
すべて開くすべて閉じるスコープ (8)
二変量ディリクレ分布から擬似乱数ベクトルのサンプルを生成する:
ディリクレ分布の一変量周辺分布はBetaDistributionに従う:
多変量周辺分布はDirichletDistributionに従う:
アプリケーション (5)
ディリクレ分布を使い多変量ポリヤ(Pólya)分布を母数混合分布として定義する:
ディリクレ分布について,Disk上で確率を求める:
単位母数のあるDirichletDistributionからサンプルを取った重みで重み推定を繰り返すことで,重み付きの分数ランダムブートストラップを信頼区間の推定に適用する:
BetaDistributionをブートストラップ母数にフィットする:
特性と関係 (2)
テキスト
Wolfram Research (2010), DirichletDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/DirichletDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "DirichletDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/DirichletDistribution.html.
APA
Wolfram Language. (2010). DirichletDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletDistribution.html