DiscreteWaveletData

DiscreteWaveletData[{wind1coef1,…},wave,wtrans]

产生离散小波数据对象，其中小波系数 coefi 对应于小波索引 windi，小波 wave 和小波变换 wtrans.

DiscreteWaveletData[{wind1coef1,…},wave,wtrans,{d1,…}]

产生离散小波数据对象，假设数据维数为 {d1,…}.

更多信息和选项

  • DiscreteWaveletData[{wind1->coef1,…},…] 总是转换为具有 DiscreteWaveletData[coefs,winds,…] 的结构的优化的标准形式.
  • 系数 coefi 可以为任意深度的 Image[…]、 Sound[…] 或 SampledSoundList[…] 对象的阵列.
  • 小波变换 wtrans 使用的选项也可以用作 DiscreteWaveletData 的选项.
  • 在标准的输出格式中，只输出简略的 wtrans，精细数和原数据的维数.
  • Normal[DiscreteWaveletData[…]] 给出规则列表 {wind1->coef1,wind2->coef2,…}，它给出小波索引 windi 与对应系数阵列 coefi 间的对应关系.
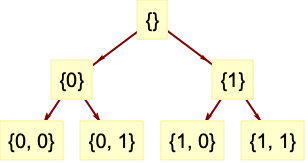
  • DiscreteWaveletData 代表一小波分解树，其中每个节点拥有小波系数. 树中的每个节点都有一个独特的小波索引向量，可用于访问小波系数.
  • 小波索引 wind 是一个整数向量. 向量的长度代表小波分解树的精细度. 对于长度为 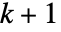的索引向量，前 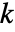个整数指明父节点，最后一个整数指明当前节点是如何与父节点相关的.
  • 对于一维数据，索引 wind 包括0和1. 0表示低通滤波器，1表示高通滤波器.
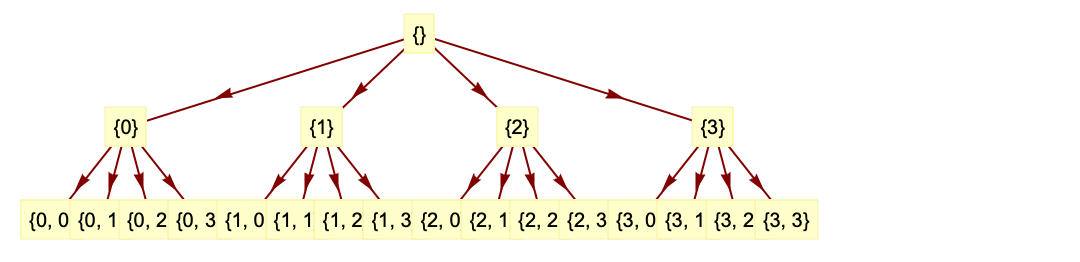
  • 对于 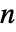维数据，索引 wind 包括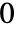到 的整数. 每个整数代表一个沿每个数据方向运行的向量，它由　 MapThread[Rule,{Range[0,2^n-1],Tuples[{lowpass,highpass},n]}] 确切给出.
  • 小波索引 wind 可以从 DiscreteWaveletData 对象 dwd 中提取小波系数. 具有以下说明：
  • dwd[wind]提取对应于 wind 的系数
    dwd[{wind1,wind2,…}]提取数个小波系数阵列
    dwd[wpatt]提取所有系数，其 wind 与模式 wpatt 匹配
    dwd[All]提取所有系数
    dwd[Automatic]提取在逆变换中使用的系数
  • 缺省情况下，系数是按 {wind1->coef1,wind2->coef2,…} 规则列表返回.
  • dwd[…,{form1,form2,…}] 可以用于控制输出形式. 可能的 formi 包括：
  • "Rules"规则 {wind1->…}
    "Values"只有系数
    "Inverse"逆变换的个别系数
    "ListPlot"一维系数的简单列表图
    "MatrixPlot"二维系数的简单矩阵图
    "Image"图像系数的图像
    "Sound"声音系数的声音对象
    "SampledSoundList"声音系数的样本声音对象
  • 可以从 DiscreteWaveletData[…]["prop"] 中获得完整的属性.
  • DiscreteWaveletData[…]["Properties"] 给出可用于 DiscreteWaveletData 对象的属性列表.
  • 与变换系数相关的属性包括：
  • "BasisIndex"逆变换中使用的小波索引
    "Dimensions"给出小波系数组的维数
    "EnergyFraction"系数组中的能量部分
    "Padding"用于变换数据的填充
    "Refinement"执行的精细度的数
    "Transform"小波变换的类型
    {"TreeView",pos}分解的树视图，具有 TreePlot 中的 pos
    "Wavelet"使用的小波族
    "WaveletIndex"所有小波索引 windi 的列表
  • 与输入数据相关的属性包括：
  • "DataDimensions"原数据的维数
    "DataChannels"数据通道数
    "DataWrapper"重建后应用于数据的包装函数
  • 包变换独有的属性包括：
  • "BestBasisBlockView"最佳基的块网格视图
    "BestBasisCostValues"每个小波系数的损失值
    "BestBasisCostTable"格式化的损失值表格
  • 从 WaveletThreshold 中可用于 dwd 的属性包括：
  • "ThresholdValues"每个小波系数的阈值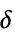
    "ThresholdTable"格式化的阈值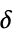
  • 可以给出下列选项：
  • Method Automatic所使用的方法
    Padding "Periodic"如何把数据扩展到边界之外
    SampleRate Automatic声音数据的采样率
    WorkingPrecision MachinePrecision内部计算所用的精度
  • Padding 的设置与 ArrayPad 中的相同.

范例

打开所有单元关闭所有单元

基本范例  (3)

从小波变换中获得 DiscreteWaveletData：

DiscreteWaveletData 代表一个变换系数的树：

提取属性，包括每个系数的总能量部分：

在其它小波函数中使用 DiscreteWaveletData 对象：

WaveletMatrixPlot[dwd] 在分层网格布局中绘制矩阵小波系数：

计算平稳小波变换系数的逆小波变换：

范围  (25)

基本用途  (8)

从诸如 DiscreteWaveletTransform 的小波变换中获得 DiscreteWaveletData：

在树布局中，显示计算得到的小波系数：

获得规则列表形式的小波阵列：

InverseWaveletTransform 作用于 DiscreteWaveletData：

对于诸如 HaarWavelet[] 的正交小波，逆变换是确切的：

提取对应于小波索引指标的系数：

以规则列表的形式给出系数：

提取对应于小波索引形式 {0,_} 的所有系数：

提取一个系数阵列列表而不是一个规则列表：

提取简单的列表图：

提取小波变换数据的属性：

所用的离散正变换、精细度的数和小波：

每个小波系数的维数：

所有可用的属性：

在其它小波函数中使用 DiscreteWaveletData：

逆变换：

小波可视化函数：

使用小波函数变换 DiscreteWaveletData：

应用阈值操作于系数：

对每个系数应用一个任意的函数：

在每个小波数据对象中绘制系数：

从给出系数阵列的规则列表中构建一个 DiscreteWaveletData：

结果代表一个包括指定系数的小波系数的树：

其它系数假设为零：

使用指定的小波和正变换的 DiscreteWaveletData：

在逆变换中使用指定的小波和正变换：

获取系数  (7)

找到哪种系数可用：

在树布局中显示所有的系数：

不同的小波索引指标从 DiscreteWaveletData 中提取系数阵列：

提取单个系数阵列：

对应于索引列表的系数：

小波索引匹配一个模式的所有系数：

索引和模式列表：

在小波逆变换中缺省使用的系数：

所有系数：

获得不同形式的系数阵列：

获得规则列表：

只获得值：

以小型列表图表示系数：

获得每个系数阵列的逆变换：

组合形式：

以小型矩阵图表示矩阵小波系数：

以小型矩阵图表示单个系数的逆变换：

获得图像小波系数，缺省情况下是应用了 ImageAdjust 的 Image 对象：

获得没有经过色彩级别调整的图像：

缺省情况下，图像小波系数是以每个色彩通道的像素值的阵列给出：

以 Audio 对象形式获取音频小波系数：

以 Audio 对象形式对单个系数进行逆变换：

获得作为 Sound 对象的声音小波系数:

作为 Sound 对象的单个系数的逆变换:

设置系数  (6)

构建 List 输入的 DiscreteWaveletData：

对于 List 系数，输入类型为 {wind1->coef1,…} 的规则列表 wrules：

执行 InverseWaveletTransform：

Image 输入：

对于 Image 系数，输入类型为 {wind1->icoef1,…} 的规则列表 irules：

执行 InverseWaveletTransform：

Sound 输入：

对于 Sound 系数，输入类型为 {wind1->scoef1,…} 的规则列表 srules：

执行 InverseWaveletTransform：

默认情况下，自动计算参数小波变换 wtrans：

指定参数小波变换 wtrans：

默认情况下，自动计算数据维数 {d1,…}：

指定数据维数：

执行简单的边缘检测:

属性  (4)

获得小波变换的属性：

使用的正变换、小波和填充方法：

精细度的数，对应于最长的小波索引：

小波系数的属性：

所有可用系数的小波索引：

不同布局的所有系数的树视图：

每个系数阵列的维数以规则列表的形式给出：

与小波基相关的属性：

在基中的小波索引：

显示在所有系数的树视图或块网格中突出的小波基：

在基系数中的信号能量分布：

由 WaveletBestBasis 计算的基的每个系数阵列的损失值:

与输入数据相关的属性:

数据维数与声音或颜色通道的数量:

自动应用于一个逆变换结果的封装函数:

选项  (7)

Method  (1)

Method 的设置与小波变换的方法相同：

生成 DiscreteWaveletData 以执行 "IntegerLifting"：

Padding  (2)

Padding 的设置与 ArrayPad 的方法相同，包括 "Periodic"：

"Reversed"：

"ReversedNegation"：

"Reflected"：

"ReflectedDifferences"：

"ReversedDifferences"：

"Extrapolated"：

默认情况下，使用 Padding->"Periodic" 选项：

SampleRate  (1)

对于 Sound 输入，自动计算 SampleRate：

默认情况下，从第一个系数规则提取 SampleRate：

明确指定 SampleRate：

WorkingPrecision  (3)

默认情况下，使用 WorkingPrecision->MachinePrecision：

使用高精度计算：

当数字与0接近时，准确度对于正确数位的数目是一个较好的指标：

使用 WorkingPrecision->∞ 进行精确计算：

应用  (3)

执行简单的无损失数据压缩：

执行小波变换：

提取小波系数用于重建：

比较 data 的 ByteCount 与相应的小波系数 wcoeff：

从压缩小波系数重建原始数据：

通过把 UnitVector 设置为在细化层 的低通系数，计算尺度函数 ：

执行 InverseWaveletTransform：

与计算所得的尺度函数比较：

通过把 UnitVector 设置为细化层 上的高通系数，计算小波函数 ：

执行 InverseWaveletTransform：

与计算所得的尺度函数比较：

属性和关系  (4)

DiscreteWaveletData 代表一个离散变换系数的树：

ContinuousWaveletData 代表在一套尺度中的连续变换系数：

根据系数和属性，重构一个 DiscreteWaveletData：

指定使用的系数、小波和正变换以及数据维数：

正变换和数据维数经常可以自动决定：

比较逆变换：

以规则列表形式获得所有系数的等效的方法：

使用 Normal：

明确地提取 All 所有系数：

指定匹配任意小波索引的模式 Blank[] (_)：

只获得对应于小波索引指标的系数阵列的等效方法：

应用 Last 于由 dwd[wind] 返回的每个规则：

使用 Part：

只明确获得系数值：

可能存在的问题  (2)

最佳基损失值只适用于来自于 WaveletBestBasis 的 DiscreteWaveletData：

首先计算最佳基代表：

多于１个的正变换可能与指定的系数相一致：

DiscreteWaveletData 选择一个一致的正变换来假设：

明确地指定正变换：

Wolfram Research (2010)，DiscreteWaveletData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.

文本

Wolfram Research (2010)，DiscreteWaveletData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.

CMS

Wolfram 语言. 2010. "DiscreteWaveletData." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.

APA

Wolfram 语言. (2010). DiscreteWaveletData. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteWaveletData.html 年

BibTeX

@misc{reference.wolfram_2024_discretewaveletdata, author="Wolfram Research", title="{DiscreteWaveletData}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discretewaveletdata, organization={Wolfram Research}, title={DiscreteWaveletData}, year={2010}, url={https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}, note=[Accessed: 05-November-2024 ]}