DiscreteWaveletData[{wind1coef1,…},wave,wtrans]
yields a discrete wavelet data object with wavelet coefficients coefi corresponding to wavelet index windi, wavelet wave, and wavelet transform wtrans.
DiscreteWaveletData[{wind1coef1,…},wave,wtrans,{d1,…}]
yields a discrete wavelet data object assuming data dimensions {d1,…}.


DiscreteWaveletData
DiscreteWaveletData[{wind1coef1,…},wave,wtrans]
yields a discrete wavelet data object with wavelet coefficients coefi corresponding to wavelet index windi, wavelet wave, and wavelet transform wtrans.
DiscreteWaveletData[{wind1coef1,…},wave,wtrans,{d1,…}]
yields a discrete wavelet data object assuming data dimensions {d1,…}.
Details and Options






- DiscreteWaveletData[{wind1->coef1,…},…] is always converted to an optimized standard form with structure DiscreteWaveletData[coefs,winds,…].
- The coefficients coefi can be arrays of any depth, Image[…], Sound[…], or SampledSoundList[…] objects.
- The options used by the wavelet transform wtrans can also be used as options to DiscreteWaveletData.
- In standard output format, only an abbreviated wtrans, the number of refinements and dimension of the original data, is printed.
- Normal[DiscreteWaveletData[…]] gives a list of rules {wind1->coef1,wind2->coef2,…} that gives the correspondence between wavelet index windi and the corresponding coefficient array coefi.
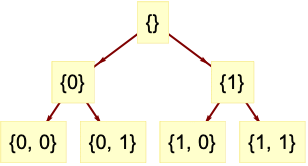
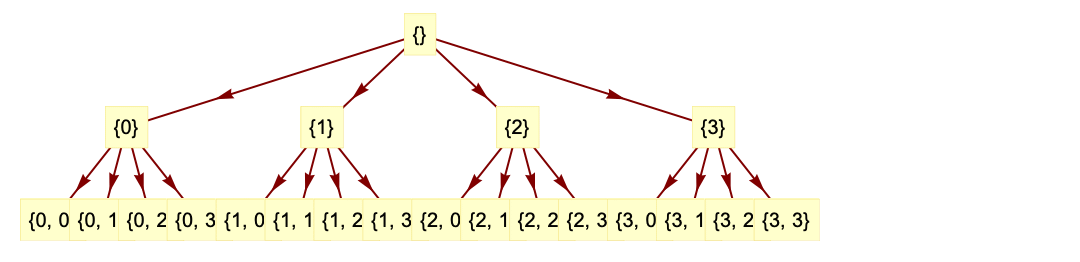
- DiscreteWaveletData represents a wavelet decomposition tree, where each node holds wavelet coefficients. Each node in the tree has a unique wavelet index vector that can be used to access wavelet coefficients.
- A wavelet index wind is a vector of integers. The length of the vector represents the refinement level in the wavelet decomposition tree. For an index vector of length
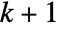 , the first
, the first 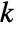 integers indicate the parent node and the last integer indicates how the current node is related to the parent node.
integers indicate the parent node and the last integer indicates how the current node is related to the parent node. - For one-dimensional data, the index wind consists of 0s and 1s. A 0 represents lowpass filtering, and a 1 represents highpass filtering.
- For
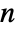 -dimensional data, the index wind consists of integers from
-dimensional data, the index wind consists of integers from 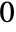 to
to 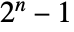 . Each integer represents a vector of operations performed along each dimension of the data, where the exact correspondence is given by MapThread[Rule,{Range[0,2^n-1],Tuples[{lowpass,highpass},n]}].
. Each integer represents a vector of operations performed along each dimension of the data, where the exact correspondence is given by MapThread[Rule,{Range[0,2^n-1],Tuples[{lowpass,highpass},n]}]. - The wavelet index wind can be used to extract wavelet coefficients from a DiscreteWaveletData object dwd. The following specifications can be given:
-
dwd[wind] extract coefficients corresponding to wind dwd[{wind1,wind2,…}] extract several wavelet coefficient arrays dwd[wpatt] extract all coefficients whose wind matches the pattern wpatt dwd[All] extract all coefficients dwd[Automatic] extract coefficients used in the inverse transform - By default, coefficients are returned as a list of rules {wind1->coef1,wind2->coef2,…}.
- dwd[…,{form1,form2,…}] can be used to control the output form. Possible formi include:
-
"Rules" rules {wind1->…} "Values" coefficients only "Inverse" inverse transform individual coefficients "ListPlot" simple list plots for 1D coefficients "MatrixPlot" simple matrix plots for 2D coefficients "Image" images for image coefficients "Sound" sound objects for sound coefficients "SampledSoundList" sampled sound objects for sound coefficients - Overall properties can be obtained from DiscreteWaveletData[…]["prop"].
- DiscreteWaveletData[…]["Properties"] gives a list of properties available for the DiscreteWaveletData object.
- Properties related to transform coefficients include:
-
"BasisIndex" wavelet indices used for inverse transform "Dimensions" give the dimensions of wavelet coefficient groups "EnergyFraction" fraction of energy in groups of coefficients "Padding" the padding used to transform data "Refinement" the number of refinement levels performed "Transform" type of wavelet transform {"TreeView",pos} tree view of decomposition, with pos as in TreePlot "Wavelet" wavelet family used "WaveletIndex" list of all wavelet indices windi - Properties related to input data include:
-
"DataDimensions" dimensions of original data "DataChannels" the number of channels of data "DataWrapper" wrapper function applied to data after reconstruction - Properties unique to packet transforms include:
-
"BestBasisBlockView" block grid view of best basis "BestBasisCostValues" cost value for each wavelet coefficient "BestBasisCostTable" formatted cost value table - Properties available for dwd from WaveletThreshold include:
-
"ThresholdValues" threshold 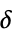 values for each wavelet coefficient
values for each wavelet coefficient"ThresholdTable" formatted threshold 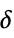 values
values - The following options can be given:
-
Method Automatic method to use Padding "Periodic" how to extend data beyond boundaries SampleRate Automatic sample rate to use for sound data WorkingPrecision MachinePrecision precision to use in internal computations - The settings for Padding are the same as those available in ArrayPad.
Examples
open all close allBasic Examples (3)
Get DiscreteWaveletData from a wavelet transform:
The DiscreteWaveletData represents a tree of transform coefficients:
Extract properties, including fraction of total energy in each coefficient:
Use DiscreteWaveletData objects in other wavelet functions:
WaveletMatrixPlot[dwd] plots matrix wavelet coefficients in a hierarchical grid layout:
Compute the inverse wavelet transform of stationary wavelet transform coefficients:
Scope (25)
Basic Uses (8)
Get a DiscreteWaveletData from wavelet transforms such as DiscreteWaveletTransform:
Show the computed wavelet coefficients in a tree layout:
Get the coefficient arrays as a list of rules:
InverseWaveletTransform operates on DiscreteWaveletData:
For orthogonal wavelets such as HaarWavelet[], the inverse transform is exact:
Extract coefficients corresponding to a wavelet index specification:
Coefficients are given as a list of rules:
Extract all coefficients corresponding to wavelet indexes of the form {0,_}:
Extract a list of the coefficient arrays instead of a list of rules:
Extract properties of the wavelet transform data:
Discrete forward transform, number of refinement levels, and wavelet used:
Dimensions of each wavelet coefficient:
Use DiscreteWaveletData in other wavelet functions:
Wavelet visualization functions:
Transform DiscreteWaveletData using wavelet functions:
Apply thresholding operation to coefficients:
Apply an arbitrary function to each coefficient:
Plot coefficients in each wavelet data object:
Construct a DiscreteWaveletData from a list of rules giving coefficient arrays:
The result represents a tree of wavelet coefficients including the specified coefficients:
The other coefficients are assumed to be zero:
Construct a DiscreteWaveletData using a specified wavelet and forward transform:
The specified wavelet and forward transform are used in the inverse transform:
Get Coefficients (7)
Find out which coefficients are available:
Show all coefficients in a tree layout:
Different wavelet index specifications to extract coefficient arrays from DiscreteWaveletData:
Extract a single coefficient array:
Coefficients corresponding to a list of indexes:
All coefficients whose wavelet index matches a pattern:
A list of indexes and patterns:
Coefficients used by default in the inverse wavelet transform:
Get coefficient arrays in different forms:
Get coefficients as small list plots:
Get inverse transform of each coefficient array:
Get matrix wavelet coefficients as small matrix plots:
Inverse transform of individual coefficients as small matrix plots:
Get image wavelet coefficients as Image objects with ImageAdjust applied by default:
Get images without color levels adjusted:
By default, image wavelet coefficients are given as arrays of pixel values for each color channel:
Get audio wavelet coefficients as Audio objects:
Inverse transform of an individual coefficient as an Audio object:
Get sound wavelet coefficients as Sound objects:
Inverse transform of individual coefficients as Sound objects:
Set Coefficients (6)
Construct a DiscreteWaveletData for List input:
For List coefficients, input a list of rules wrules of the type {wind1->coef1,…}:
Perform an InverseWaveletTransform:
Image input:
For Image coefficients, input a list of rules irules of the type {wind1->icoef1,…}:
Perform an InverseWaveletTransform:
Sound input:
For Sound coefficients, input a list of rules srules of the type {wind1->scoef1,…}:
Perform an InverseWaveletTransform:
By default, parameter wavelet transform wtrans is computed automatically:
Specify parameter wavelet transform wtrans:
By default, data dimensions {d1,…} are computed automatically:
Properties (4)
Get properties of the wavelet transform:
Forward transform, wavelet, and padding method used:
Number of levels of refinement, corresponding to longest wavelet index:
Properties of wavelet coefficients:
Wavelet indexes for all available coefficients:
Tree view of all coefficients with different layouts:
Dimensions of each coefficient array as a list of rules:
Properties related to wavelet basis:
Show wavelet basis highlighted in a tree view or block grid of all coefficients:
Distribution of signal energy among basis coefficients:
Cost values of each coefficient array for bases computed by WaveletBestBasis:
Properties related to input data:
Data dimensions and number of audio or color channels:
Wrapper function that is automatically applied to the result of an inverse transform:
Options (7)
Method (1)
The settings for Method are the same as the methods for wavelet transforms:
Generate DiscreteWaveletData to perform "IntegerLifting":
Padding (2)
SampleRate (1)
For Sound input, SampleRate is automatically computed:
By default SampleRate is extracted from the first coefficient rule:
Specify SampleRate explicitly:
WorkingPrecision (3)
By default, WorkingPrecision->MachinePrecision is used:
Use higher-precision computation:
With numbers close to zero, accuracy is the better indicator of the number of correct digits:
Use WorkingPrecision->∞ for exact computation:
Applications (3)
Perform simple lossless data compression:
Extract wavelet coefficients used for reconstruction:
Compare ByteCount for data and its corresponding wavelet coefficients wcoeff:
Reconstruct original data from compressed wavelet coefficients:
Compute scaling function ![]() by setting a UnitVector as a lowpass coefficient at refinement level
by setting a UnitVector as a lowpass coefficient at refinement level ![]() :
:
Perform an InverseWaveletTransform:
Compare with the computed scaling function:
Compute wavelet function ![]() by setting a UnitVector as a highpass coefficient at refinement level
by setting a UnitVector as a highpass coefficient at refinement level ![]() :
:
Perform an InverseWaveletTransform:
Properties & Relations (4)
DiscreteWaveletData represents a tree of discrete transform coefficients:
ContinuousWaveletData represents continuous transform coefficients at a set of scales:
Reconstruct a DiscreteWaveletData from its coefficients and properties:
Specify the coefficients, the wavelet and forward transform used, and the data dimensions:
The forward transform and data dimensions can often be determined automatically:
Equivalent ways to get all coefficients as a list of rules:
Use Normal:
Explicitly extract All coefficients:
Specify the pattern Blank[] (_), which matches any wavelet index:
Equivalent ways to get only coefficient arrays corresponding to a wavelet index specification:
Apply Last to each rule returned by dwd[wind]:
Use Part![]()
Possible Issues (2)
Best basis cost values are only available for DiscreteWaveletData from WaveletBestBasis:
Compute a best basis representation first:
More than one forward transform may be consistent with the specified coefficients:
DiscreteWaveletData chooses one consistent forward transform to assume:
Related Guides
History
Text
Wolfram Research (2010), DiscreteWaveletData, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.
CMS
Wolfram Language. 2010. "DiscreteWaveletData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.
APA
Wolfram Language. (2010). DiscreteWaveletData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteWaveletData.html
BibTeX
@misc{reference.wolfram_2025_discretewaveletdata, author="Wolfram Research", title="{DiscreteWaveletData}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretewaveletdata, organization={Wolfram Research}, title={DiscreteWaveletData}, year={2010}, url={https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}, note=[Accessed: 01-March-2026]}