Eigenvalues[m]
正方行列 m の固有値のリストを与える.
Eigenvalues[{m,a}]
a について m の一般化された固有値を与える.
Eigenvalues[m,k]
m の最初の k 個の固有値を与える.
Eigenvalues[{m,a},k]
最初の k 個の一般化された固有値を与える.


Eigenvalues
Eigenvalues[m]
正方行列 m の固有値のリストを与える.
Eigenvalues[{m,a}]
a について m の一般化された固有値を与える.
Eigenvalues[m,k]
m の最初の k 個の固有値を与える.
Eigenvalues[{m,a},k]
最初の k 個の一般化された固有値を与える.
詳細とオプション


- 行列 m が近似実数または近似複素数を含むとき,Eigenvaluesは数値固有値を計算する.
- 固有値が適切な多重度に従って繰り返し出現する.
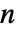 ×
×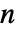 行列は,厳密に
行列は,厳密に 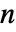 個の固有値のリストを返すが,それらが異なっているとは限らない.
個の固有値のリストを返すが,それらが異なっているとは限らない.- 固有値は,数値的な場合は絶対値が大きいものから小さいものへの順に並べられる.
- 行列 m の固有値は,非零の固有ベクトル
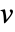 について
について 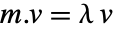 となるような
となるような 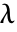 である. »
である. » - a についての m の一般化された有限固有値は
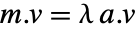 となるような
となるような 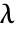 である. »
である. » - 通常固有値は常に有限であるが,一般化された固有値は無限となり得る.
- 行列 m と a が次元
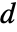 の共通の零空間を持っているとき,これらの一般化された固有値の
の共通の零空間を持っているとき,これらの一般化された固有値の 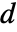 はIndeterminateになる. »
はIndeterminateになる. » - 数値的な固有値の場合,Eigenvalues[m,k]は絶対値で最大となる k を与える.
- Eigenvalues[m,-k]は絶対値で最小となる k を与える.
- Eigenvalues[m,spec]は常にTake[Eigenvalues[m],spec]と等価である.
- Eigenvalues[m,UpTo[k]]は,固有値を k 個,あるいはできるだけたくさん与える.
- SparseArrayオブジェクトと構造化配列をEigenvaluesで使うことができる.
- Eigenvaluesのオプションと設定値
-
Cubics False 三次方程式を解く際に累乗根を使うかどうか Method Automatic 使用するメソッド Quartics False 四次方程式を解く際に累乗根を使うかどうか - 近似数値行列についての明示的なMethod設定
-
"Arnoldi" いくつかの固有値を求めるためのArnoldi反復法 "Banded" エルミート行列のための直接帯行列ソルバ "Direct" 全固有値を求めるための直接法 "FEAST" 区間内の固有値を求めるためのFEAST反復法(エルミート行列のみに適用可) - "Arnoldi"法は,対称行列あるいはエルミート行列に適用された際には,Lanczos法としても知られている.
- "Arnoldi"法および"FEAST"法は,サブオプションMethod->{"name",opt1->val1,…}を取る.これは,Methodのサブセクションで見ることができる.
例題
すべて開く すべて閉じるスコープ (20)
基本的な用法 (6)
固有値の部分集合 (5)
特殊行列 (5)
QuantityArrayオブジェクトの単位は固有値に存在し,固有ベクトル自体は無次元である:
IdentityMatrix[n]は常にすべて1の固有値を持つ:
HilbertMatrixの固有値:
CenteredInterval行列の固有値:
オプション (11)
Cubics (1)
EigenvaluesはRootを使って厳密な固有値を計算する:
Method (9)
"Arnoldi" (6)
Arnoldi法は,機械精度および任意精度の行列に使うことができる.Arnoldi法の実装は,"ARPACK"ライブラリに基づいている.これは,大規模な疎行列に最も有効である.
"Arnoldi"法では,以下のサブオプションを指定することができる.
| "BasisSize" | Arnoldi基底の大きさ | |
| "Criteria" | 使用する基準 | |
| "MaxIterations" | ||
| "Shift" | ||
| "StartingVector" | ||
| "Tolerance" | 反復の終了に使用される許容度 |
| "Magnitude" | Absに基づく | |
| "RealPart" | Reに基づく | |
| "ImaginaryPart" | Imに基づく | |
| "BothEnds" | 実数値対称行列スペクトルの両端からのいくつかの固有値 |
さまざまな"Criteria"設定を使って最大固有値を計算する.行列 m は,固有値![]() を持つ:
を持つ:
デフォルトで,"Criteria"->"Magnitude"は最大規模の固有値を選ぶ:
"Shift"->μ を使い,行列 ![]() を
を ![]() に変換することで固有値をシフトさせる.これで固有ベクトルが保存されるが,固有値は-μ 変化する.このメソッドは,変化した固有値を相殺する."Shift"は,一般に,最大あるいは最小規模といった選択基準なしで固有ペアを求める際に使われる:
に変換することで固有値をシフトさせる.これで固有ベクトルが保存されるが,固有値は-μ 変化する.このメソッドは,変化した固有値を相殺する."Shift"は,一般に,最大あるいは最小規模といった選択基準なしで固有ペアを求める際に使われる:
"Banded" (1)
アプリケーション (15)
固有値の幾何学 (3)
正の固有値を持つ固有ベクトルは,行列の作用を受けたときに同じ方向を指す:
負の固有値を持つ固有ベクトルは,行列の作用を受けたときに逆の方向を指す:
CoefficientArraysを使って二次形式の対称行列を得る:
対角化 (4)
これで,行列の任意の関数が ![]() として計算できるようになった.例えばMatrixPower:
として計算できるようになった.例えばMatrixPower:
同様に,MatrixExpが自明となって ![]() の対角要素を累乗することしか必要としなくなった:
の対角要素を累乗することしか必要としなくなった:
![]() を,その標準行列が行列
を,その標準行列が行列 ![]() で与えられる線形変換とする.基底
で与えられる線形変換とする.基底![]() における
における ![]() の表現が対角であるという特性を持つ
の表現が対角であるという特性を持つ![]() の基底
の基底 ![]() を求める:
を求める:
![]() が固有ベクトルからなり,
が固有ベクトルからなり,![]() が列が
が列が ![]() の要素である行列であるとする:
の要素である行列であるとする:
![]() は
は ![]() の座標から標準座標に変換する.この逆変換は逆方向に変換する:
の座標から標準座標に変換する.この逆変換は逆方向に変換する:
実対称行列は,![]() のように直交対角化可能である.ただし,
のように直交対角化可能である.ただし,![]() は実対角行列であり
は実対角行列であり ![]() は直交行列である.次の行列が対象であることを確認し,次にこれを対角化する:
は直交行列である.次の行列が対象であることを確認し,次にこれを対角化する:
直交行列については,固有ベクトルを列に置く前に正規化する必要がある:
![]() のとき,その行列は正規行列と呼ばれる.正規行列はユニタリ変換で対角化できる最も一般的な行列である.実対称行列
のとき,その行列は正規行列と呼ばれる.正規行列はユニタリ変換で対角化できる最も一般的な行列である.実対称行列 ![]() は,方程式の両辺が
は,方程式の両辺が ![]() なので,すべて正規行列である:
なので,すべて正規行列である:
NormalMatrixQを使って確認する:
微分方程式と動的な系 (4)
常微分方程式の系 ![]() ,
, ![]() ,
, ![]() を解く.まず,右辺のために係数行列
を解く.まず,右辺のために係数行列 ![]() を構築する:
を構築する:
DSolveValueを使って解を確かめる:
粒子が平面の力場で動いており,その位置ベクトル ![]() が
が ![]() と
と ![]() を満足するとする.ただし,
を満足するとする.ただし,![]() と
と ![]() は以下であるとする.
は以下であるとする.![]() のときのこの初期値問題を解く:
のときのこの初期値問題を解く:
系の一般解は ![]() である.LinearSolveを使って係数を決定する:
である.LinearSolveを使って係数を決定する:
DSolveValueを使って解を確かめる:
固有値と固有ベクトルを求め,Chopを使って小さい数値誤差を切り捨てる:
物理 (4)
量子力学では,状態はエルミート線形演算子による複素単位ベクトルと物理量で表される.固有値は可能な観測値を表,固有ベクトルに関する成分の二乗係数をはそれらの観測値の確率を表す.与えられたスピン演算子 ![]() と状態
と状態 ![]() について,可能な観測値とその確率を求める:
について,可能な観測値とその確率を求める:
量子力学では,エネルギー演算子はハミルトニアン ![]() と呼ばれ,エネルギーが
と呼ばれ,エネルギーが ![]() の状態はシュレーディンガー方程式
の状態はシュレーディンガー方程式 ![]() に従って進化する.一定磁場で
に従って進化する.一定磁場で ![]() 方向にスピン1粒子に対するハミルトニアンが与えられたとして,初期状態が
方向にスピン1粒子に対するハミルトニアンが与えられたとして,初期状態が ![]() を表す状態
を表す状態![]() であった粒子の時点
であった粒子の時点 ![]() における状態を求める:
における状態を求める:
時点 ![]() における状態はシュレーディンガー方程式に従って進化する各固有状態の和である:
における状態はシュレーディンガー方程式に従って進化する各固有状態の和である:
慣性モーメントはさまざまな方向への回転に対する剛体の抵抗を表す実対称行列である.この行列の固有値は主慣性モーメントと呼ばれ,対応する固有ベクトル(必然的の直交ベクトル)は主軸である.以下の四面体の主慣性モーメントと主軸を求める:
一般化された固有系を使って項を分離するための練成振動の正規モードを求めることができる.以下の図に示した系について考える:
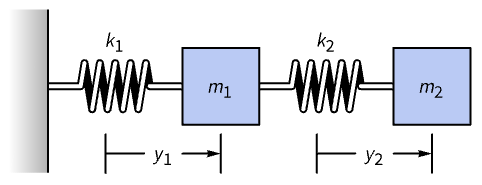
フックの法則によると,これは![]() と
と ![]() に従う.一般解の
に従う.一般解の ![]() を代入すると,以下のように,剛性行列
を代入すると,以下のように,剛性行列 ![]() ,質量行列
,質量行列 ![]() の行列方程式
の行列方程式 ![]() が与えられる:
が与えられる:
特性と関係 (15)
Eigenvalues[m]は,事実上,Eigensystemが返す対の最初の要素である:
固有ベクトルと固有値の両方が必要な場合は,Eigensystemを呼び出した方が効率的なことが多い:
CharacteristicPolynomialで多項式を計算する:
一般化された無限固有値は ![]() である
である ![]() の固有ベクトル
の固有ベクトル ![]() に相当する:
に相当する:
m の固有値の積はDet[m]に等しい:
m の固有値の和はTr[m]に等しい:
![]() がすべて異なる固有値を持つなら,DiagonalizableMatrixQ[m]はTrueを与える:
がすべて異なる固有値を持つなら,DiagonalizableMatrixQ[m]はTrueを与える:
Eigenvaluesは絶対値でソートするので,以下は同じ値を与えるが順序は逆である:
解析関数 ![]() について,
について,![]() の固有値は
の固有値は ![]() を
を ![]() の固有値
の固有値 ![]() に適用した結果である:
に適用した結果である:
SingularValueList[m]は非零の固有値 ![]() の平方根に等しい:
の平方根に等しい:
JordanDecomposition[m]は固有値と固有ベクトルから構築された行列![]() を返す:
を返す:
![]() 行列は固有値の項と対角にあり,おそらくEigensystemとは次数が異なる:
行列は固有値の項と対角にあり,おそらくEigensystemとは次数が異なる:
数値正規行列 ![]() のSchurDecomposition[n,RealBlockDiagonalFormFalse]:
のSchurDecomposition[n,RealBlockDiagonalFormFalse]:
t 行列は対角行列で固有値の項を持ち,おそらくEigensystemとは次数が異なる:
行列が次元 ![]() のヌル空間を共有するなら,それらの一般化された固有値の
のヌル空間を共有するなら,それらの一般化された固有値の ![]() はIndeterminateである:
はIndeterminateである:
![]() のそれ自身に対する二つの一般化された固有値はIndeterminateである:
のそれ自身に対する二つの一般化された固有値はIndeterminateである:
したがって,![]() の
の ![]() についての一般化された1つの固有値はIndeterminateである:
についての一般化された1つの固有値はIndeterminateである:
考えられる問題 (5)
EigenvaluesとEigenvectorsは,対応する順序で結果を与える保証はない:
以下の特定の例では,7番目の固有ベクトルは7番目の固有値に対応しない:
Eigensystem[mat]を使って対応する結果が常に一致するようにする:
固有値が密接にグループ化されている場合は,疎行列に対する反復的な方法が収束しないことがある:

収束を加速するために,期待値の近くでアルゴリズムをシフトさせることができる:
テクニカルノート
-
▪
- ベクトルと行列 ▪
- 固有値と固有ベクトル
関連するガイド
-
▪
- 行列の操作 ▪
- 行列と線形代数 ▪
- 行列分解 ▪
- グラフプログラミング
履歴
1988 で導入 (1.0) | 2003 で更新 (5.0) ▪ 2014 (10.0) ▪ 2015 (10.3) ▪ 2024 (14.0)
テキスト
Wolfram Research (1988), Eigenvalues, Wolfram言語関数, https://reference.wolfram.com/language/ref/Eigenvalues.html (2024年に更新).
CMS
Wolfram Language. 1988. "Eigenvalues." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Eigenvalues.html.
APA
Wolfram Language. (1988). Eigenvalues. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Eigenvalues.html
BibTeX
@misc{reference.wolfram_2025_eigenvalues, author="Wolfram Research", title="{Eigenvalues}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Eigenvalues.html}", note=[Accessed: 07-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_eigenvalues, organization={Wolfram Research}, title={Eigenvalues}, year={2024}, url={https://reference.wolfram.com/language/ref/Eigenvalues.html}, note=[Accessed: 07-December-2025]}