ExtremeValueDistribution
位置母数 α,尺度母数 β の極値分布を表す.
位置母数0,尺度母数1の極値分布を表す.
詳細

- 極値分布は,正規分布等の分布からサンプルしたものの最大値の漸近分布を与える.
- 極値分布における値
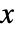 の確率密度は,
の確率密度は,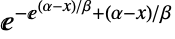 に比例する. »
に比例する. » - 最小値の漸近分布は,極値分布とも呼ばれるものだが,Wolfram言語にはGumbelDistributionとして実装されている. »
- ExtremeValueDistributionでは,α は任意の実数で,β は任意の正の実数でよい.
- ExtremeValueDistributionでは,α と β は同じ単位次元の任意の数量でよい. »
- ExtremeValueDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- ExtremeValueDistribution[α,β]は,実数集合上で定義され,実数 α(「位置母数」と呼ばれる),正の実数 β(「尺度母数」と呼ばれる)でパラメータ化される連続統計分布を表す.極値分布の確率密度関数(PDF)の全体的な動作は平滑かつ単峰性であるが,母数 α と β がPDFの水平位置と全体的な高さおよび傾きをそれぞれ決定する.これに加え,PDFの裾部は,PDFが
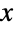 の大きい値について指数的に減少するという意味で「薄い」(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にできる).極値分布はタイプIの極値分布,二重指数分布(やはり二重指数と呼ばれることがあるLaplaceDistributionと混同しないように),対数ワイブル分布(WeibullDistribution),ガンベル型分布(GumbelDistributionと混同しないように)とも呼ばれることがある.
の大きい値について指数的に減少するという意味で「薄い」(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にできる).極値分布はタイプIの極値分布,二重指数分布(やはり二重指数と呼ばれることがあるLaplaceDistributionと混同しないように),対数ワイブル分布(WeibullDistribution),ガンベル型分布(GumbelDistributionと混同しないように)とも呼ばれることがある. - ExtremeValueDistributionは極値分布と呼ばれる分布であるが,実際は「極値分布」として分類される4つの極値分布の1つ(他の3つはGumbelDistribution,FrechetDistribution,WeibullDistribution)である.極値分布は次第に大きくなるランダムなサンプルの最大値の極限分布として得ることができる.PDFが二重に指数的(つまりExp[-Exp[…]]の形をしている)ので,分布のグラフにはより誇張された特徴(例えば,より高い峰やより薄い裾部)つまり,これらの分布に一意的な特徴が見られる.この分布は,1920年代初頭に,天文学で異常値を拒絶あるいは利用する必要に対応するために導入された.極値理論として知られる分野の基盤である極値分布は,異常洪水,壊滅的な保険の損失,大規模な山火事等の「起る可能性が極めて低い」状況(つまり,データ集合が中央値から極端に逸脱している変量からなる状況)を説明するのに広く使われてきた.さらに,極値分布は,生物学における進化論的な遺伝子の突然変異をモデル化するツールとしても使うことができる.
- RandomVariateを使って極値分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,ExtremeValueDistribution[α,β]](より簡略すると xExtremeValueDistribution[α,β])を使って,確率変数 x が,極値分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[ExtremeValueDistribution[α,β],x]およびCDF[ExtremeValueDistribution[α,β],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が極値分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック極値分布を推定することが,FindDistributionParametersを使ってデータを極値分布にフィットすることができる.ProbabilityPlotを使って記号極値分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号極値分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された極値分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って極値分布を含む高次元分布を構築することが,ProductDistributionを使って極値分布を含む独立成分分布の結合分布を計算することができる.
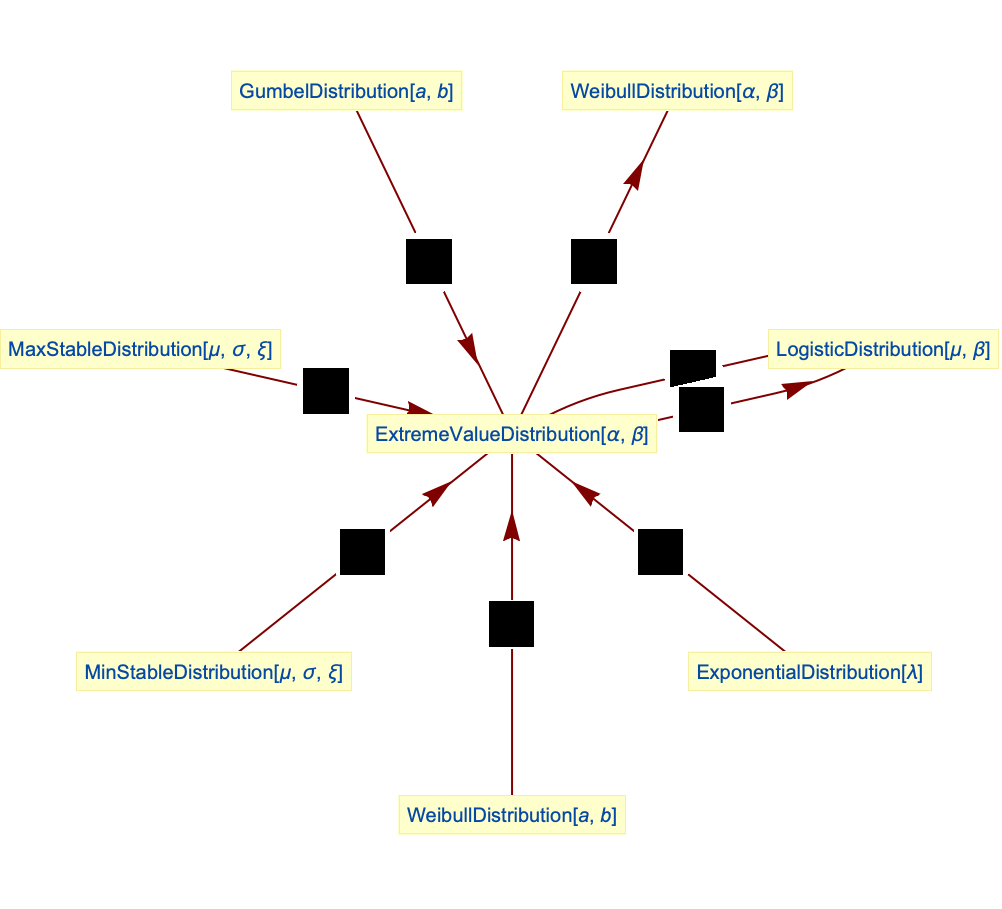
- 極値分布は他の数多くの分布と関連がある.先述したように,ExtremeValueDistributionは,起る可能性が極めて低い事象の説明に用いられる,GumbelDistribution,FrechetDistribution,WeibullDistribution等の数多くの分布の1つである.この定性的な関係は,ExtremeValueDistribution[α,β]のPDFがTransformedDistribution[-β α Log[u/β]+α,u WeibullDistribution[α,β]]やTransformedDistribution[-β α Log[u/β]+α,u WeibullDistribution[α,β]]のそれと厳密に等しいように,数量的な成分も併せ持つ.ExtremeValueDistributionはExponentialDistributionおよびMinStableDistributionの変換で,ExtremeValueDistribution[α,β]のPDFがMaxStableDistribution[α,β,0]のそれと等しいという意味で,MaxStableDistributionの特殊ケースである.ExtremeValueDistributionは,ExpGammaDistribution,ExponentialDistribution,LogisticDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
寿命が極値分布に従うデバイスがある.このデバイスの信頼性を求める:
ExtremeValueDistributionを使って月間最大風速をモデル化することができる.次は,1950年1月から2009年12月までに記録されたマサチューセッツ州ボストンの月間最大風速(km/h)である:
特性と関係 (16)
極値分布は平行移動と正の因子によるスケーリングの下では閉じている:
歪度はGumbelDistributionの歪度に負号を付けたものである:
ExtremeValueDistributionは右に歪み,GumbelDistributionは左に歪んでいる:
尖度はGumbelDistributionの尖度に等しい:
ExtremeValueDistributionはMaxを取る際に閉じている:
ExtremeValueDistributionのCDFは安定性の仮定の方程式を解く:
ExtremeValueDistributionはGumbelDistributionの否定である:
ExtremeValueDistributionはWeibullDistributionを変換したものである:
WeibullDistributionは極値分布を変換したものである:
極値分布はMaxStableDistributionの特殊ケースである:
極値分布はMinStableDistributionを変換したものである:
極値分布はExponentialDistributionを変換したものである:
極値分布に従う2変量の差はGumbelDistributionに従う2変量の差が従う分布,すなわちLogisticDistributionに従う:
極値分布とGumbelDistributionの和はLogisticDistributionに従う:
LogisticDistributionは極値分布のParameterMixtureDistributionである:
ExponentialDistributionおよびExtremeValueDistributionの最大値はShiftedGompertzDistributionに従う:
考えられる問題 (3)
最大値の分布はExtremeValueDistributionで与えられる:
最小値の分布はGumbelDistributionで与えられる:
ExtremeValueDistributionは,α が実数ではないときは定義されない:
ExtremeValueDistributionは,β が正の実数ではないときは定義されない:
テキスト
Wolfram Research (2007), ExtremeValueDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "ExtremeValueDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html.
APA
Wolfram Language. (2007). ExtremeValueDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html