FisherHypergeometricDistribution

✖
`FisherHypergeometricDistribution`

✖

FisherHypergeometricDistribution[n,n_succ,n_tot,w]

represents a Fisher noncentral hypergeometric distribution.

Details

A Fisher hypergeometric distribution gives the distribution of the number of successes in n independent draws from a population of size n_tot containing n_succ successes with the odds ratio w.
FisherHypergeometricDistribution allows n, n_succ, and n_tot to be any integers such that 0<n≤n_tot, and 0≤n_succ≤n_tot, and w is any positive real number.
FisherHypergeometricDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

FisherHypergeometricDistribution[n,n_succ,n_tot,w] represents a discrete statistical distribution defined for integer values 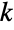contained in and determined by four parameters n, n_succ, n_tot, and w. In particular, w is a real number representing the odds ratio of the experiment described by the Fisher hypergeometric distribution, while n, n_succ, and n_tot are integers satisfying 0<n≤n_tot and 0≤n_succ≤n_tot and indicating the number of draws of the experiment, the number of successes within that population, and the size of the population drawn from, respectively. The Fisher hypergeometric distribution has a probability density function (PDF) that is discrete, unimodal, and sometimes referred to as Fisher's noncentral hypergeometric distribution in order to differentiate it from the (central) hypergeometric distribution (HypergeometricDistribution).
Fisher's hypergeometric distribution can be illustrated using a particularly defined urn model containing n_succ blue balls and n_tot-n_succ green balls having weights w₁ and w₂, respectively. From this urn, n balls are known to be drawn at random and so that the probability of taking a particular ball is proportional to its weight but is independent from what happens to the other balls. Under this construction, the conditional distribution modeling the number of taken blue balls given n is modeled by Fisher's hypergeometric distribution with 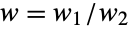. Note that this model is almost identical to the urn model defining WalleniusHypergeometricDistribution, with the exception that the latter is modeled by a drawing procedure that fails to be independent, and that the drawing procedure described above is such that each draw is distributed according to BinomialDistribution.
A number of real-world phenomena can be modeled using a Fisher hypergeometric distribution. For example, the distribution has been shown to model the deaths of species competing for a limited food resource (assuming the fates of the species members are independent of one another). Fisher's hypergeometric distribution is also important to the theory of Monte Carlo simulations and can be used to perform statistical tests on contingency tables.
RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Fisher hypergeometric distribution. Distributed[x,FisherHypergeometricDistribution[n,n_succ,n_tot,w]], written more concisely as xFisherHypergeometricDistribution[n,n_succ,n_tot,w], can be used to assert that a random variable x is distributed according to a Fisher hypergeometric distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
The probability density and cumulative distribution functions may be given using PDF[FisherHypergeometricDistribution[n,n_succ,n_tot,w],x] and CDF[FisherHypergeometricDistribution[n,n_succ,n_tot,w],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
DistributionFitTest can be used to test if a given dataset is consistent with a Fisher hypergeometric distribution, EstimatedDistribution to estimate a Fisher hypergeometric parametric distribution from given data, and FindDistributionParameters to fit data to a Fisher hypergeometric distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Fisher hypergeometric distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Fisher hypergeometric distribution.
TransformedDistribution can be used to represent a transformed Fisher hypergeometric distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Fisher hypergeometric distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Fisher hypergeometric distributions.
FisherHypergeometricDistribution is related to a number of other statistical distributions. As mentioned above, there is a fundamental link between FisherHypergeometricDistribution, WalleniusHypergeometricDistribution, and HypergeometricDistribution. The latter relationship can be made quantitatively precise by noting that FisherHypergeometricDistribution[n,n_succ,n_tot,1] has the same PDF as HypergeometricDistribution[n,n_succ,n_tot]. In addition, FisherHypergeometricDistribution can be obtained from two independent samples distributed according to BinomialDistribution by conditioning on their total.

Examples

open allclose all

Basic Examples (3)Summary of the most common use cases

Probability mass function:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-gajfag

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-z1tsez

Out[2]=2

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-185xgp

Out[1]=1

Cumulative distribution function:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-j3pm1y

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-byyz6l

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-o0ofzy

Out[3]=3

Mean:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-ynu7n

Out[1]=1

Scope (5)Survey of the scope of standard use cases

Generate a sample of pseudorandom numbers from a noncentral hypergeometric distribution:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-qhtk5j

Compare its histogram to the PDF:

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-03mwaz

Out[2]=2

Distribution parameters estimation:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-45b7g2

Estimate the distribution parameters from sample data:

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-epi747

Out[2]=2

Compare the density histogram of the sample with the PDF of the estimated distribution:

In[3]:=3

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-f8ui5o

Out[3]=3

Different moments with closed forms as functions of parameters:

Moment:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-zppkee

Out[1]=1

CentralMoment:

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-o6i3hc

Out[2]=2

FactorialMoment:

In[3]:=3

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-zg9ct4

Out[3]=3

Closed form for symbolic order:

In[4]:=4

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-fqv8sj

Out[4]=4

Cumulant:

In[5]:=5

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-9gzmth

Out[5]=5

Hazard function:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-7tmr9u

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-beq3rh

Out[2]=2

Quantile function:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-f5db4g

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-bzwvpb

Out[2]=2

Applications (2)Sample problems that can be solved with this function

CDF of FisherHypergeometricDistribution is an example of a right-continuous function:

In[1]:=1

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-5w2lx5

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/01lgynmsxg1t8rh46-q2wu5i

Out[2]=2

An urn contains red balls of weight and blue balls of weight . With balls drawn independently, the probability of drawing a red or blue ball depends on its weight. If , , , , and , find the distribution of the number of red balls drawn: