FisherHypergeometricDistribution

FisherHypergeometricDistribution[n,nsucc,ntot,w]

フィッシャー(Fisher)の非心超幾何分布を表す．

詳細

  • フィッシャーの超幾何分布は，オッズ比 w でnsucc回の成功を含む大きさが ntotの母集団から自由に n 回引いた場合の成功回数の分布を与える．
  • FisherHypergeometricDistributionでは，n，nsucc，ntot は0<n≤ntotで0≤nsucc≤ntotとなる任意の整数でよく，w は任意の正の実数でよい．
  • FisherHypergeometricDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • FisherHypergeometricDistribution[n,nsucc,ntot,w]は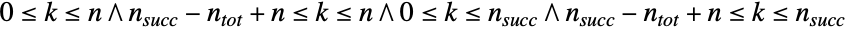，に含まれる整数値 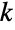によって定義され，n，nsucc，ntot，w の4つの母数によって決定される離散統計分布である．w はフィッシャーの超幾何分布によって説明される実験のオッズ比を表す実数である．n，nsucc，ntotは，0<n≤ntotおよび0≤nsucc≤ntotを満足する整数で，実験の抽出回数，母集団についての成功回数，そこから抽出する母集団の大きさをそれぞれ表す．フィッシャーの超幾何分布の確率密度関数(PDF)は，離散単峰性で，（中心）超幾何分布(HypergeometricDistribution)と区別するためにフィッシャーの非心超幾何分布と呼ばれることがある．
  • フッシャーの超幾何分布は，nsucc個の青いボール（重み w1）と ntot-nsucc個の緑のボール（重み w2）の入った，特別に定義された壷モデルを使って説明することができる．この壷から n 個のボールを無作為に取り出す．特定のボールを取り出す確率はその重みに比例するが，他のボールに起ることからは独立している．この構造では，n で与えられる取り出された青いボールの数をモデル化する条件付き分布は，フィッシャーの超幾何分布(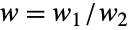)でモデル化される．このモデルがWalleniusHypergeometricDistributionを定義する壷モデルとほぼ等しいことに注意されたい．違いは，後者が独立ではない抽出手続きで描写され，上で説明した抽出手続きでは，1回ごとのボールの抽出がBinomialDistributionに従っている点である．
  • 数多くの現実世界の現象が，フィッシャーの超幾何分布を使ってモデル化できる．例えば，この分布は限られた食料源を競い合う種の死をモデル化することが知られている（種の成員の運命は互いに独立していると仮定する）．フィッシャーの超幾何分布はモンテカルロシミュレーションにとっても重要であり，分割表についての統計検定の実行に使うことができる．
  • RandomVariateを使ってフィッシャーの超幾何分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,FisherHypergeometricDistribution[n,nsucc,ntot,w]]（より簡略すると xFisherHypergeometricDistribution[n,nsucc,ntot,w]）を使って，確率変数 x が，フィッシャーの超幾何分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[FisherHypergeometricDistribution[n,nsucc,ntot,w],x]およびCDF[FisherHypergeometricDistribution[n,nsucc,ntot,w],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．これらの数量は，DiscretePlotを使って可視化することができる．
  • DistributionFitTestを使って，与えられたデータ集合がフィッシャーの超幾何分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからフィッシャーのパラメトリック超幾何分布を推定することが，FindDistributionParametersを使ってデータをフィッシャーの超幾何分布にフィットすることができる．ProbabilityPlotを使ってフィッシャーの記号超幾何分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使ってフィッシャーの記号超幾何分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたフィッシャーの超幾何分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってフィッシャーの超幾何分布を含む高次元分布を構築することが，ProductDistributionを使ってフィッシャーの超幾何分布を含む独立成分分布の結合分布を計算することができる．
  • FisherHypergeometricDistributionは，数多くの他の統計分布と関連がある．上述のように，FisherHypergeometricDistribution，WalleniusHypergeometricDistribution，HypergeometricDistributionとの間には基本的な繋がりがある．後者の関係は，FisherHypergeometricDistribution[n,nsucc,ntot,1]とHypergeometricDistribution[n,nsucc,ntot]のPDFが等しいことに注目することで数量的に正確にすることができる．加えて，FisherHypergeometricDistributionはBinomialDistributionに従って分布している2つの独立サンプルから，その合計に制限を加えることで，得ることができる．

例題

すべて開くすべて閉じる

例  (3)

確率質量関数：

累積分布関数：

平均：

スコープ  (5)

超幾何分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

記号次数の閉形式：

Cumulant：

ハザード関数：

分位関数：

アプリケーション  (2)

FisherHypergeometricDistributionのCDFは右連続関数の例である：

重み の 個の赤いボールと重み の 個の青いボール入った壷がある． 個のボールを別々に取り出したとき，赤または青のボールに当たる確率はその重みによる．，，，，として赤いボールを取り出す数の分布を求める：

少なくとも3個の赤いボールを取り出す確率を求める：

赤いボールの平均数を求める：

12個のボールを取り出すことを連続して30回行った場合の赤いボールの数のシミュレーションを行う：

特性と関係  (3)

他の分布との関係：

HypergeometricDistributionは特殊なケースである：

FisherHypergeometricDistributionは，両者の合計に条件を付けた上で，2つの独立二項変数から得られる：

Wolfram Research (2010), FisherHypergeometricDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

テキスト

Wolfram Research (2010), FisherHypergeometricDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

CMS

Wolfram Language. 2010. "FisherHypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

APA

Wolfram Language. (2010). FisherHypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html

BibTeX

@misc{reference.wolfram_2024_fisherhypergeometricdistribution, author="Wolfram Research", title="{FisherHypergeometricDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fisherhypergeometricdistribution, organization={Wolfram Research}, title={FisherHypergeometricDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html}, note=[Accessed: 22-November-2024 ]}