FisherHypergeometricDistribution

FisherHypergeometricDistribution[n,nsucc,ntot,w]

表示一个 Fisher 非中心超几何分布.

更多信息

背景

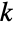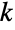  • FisherHypergeometricDistribution[n,nsucc,ntot,w] 表示一个离散统计分布，定义在整数值 上， 属于满足 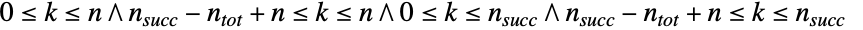，由四个参数 n、nsucc、ntot 和 w 决定. 具体来说，w 是一个实数，表示由 Fisher 超几何分布所描述的实验的优势比，而 n、nsucc 和 ntot 为满足 0<n≤ntot 和 0≤nsucc≤ntot 的整数，分别表示实验的样本数、总体中成功的数量以及总体的数量. Fisher 超几何分布的概率密度函数（PDF）是离散的、单峰的，有时，为了和（中心）超几何分布（HypergeometricDistribution）区别开，称其为 Fisher 非中心超几何分布.
  • 可以用一个专门定义的瓮模型来说明 Fisher 超几何分布，模型包含 nsucc 个蓝球和 ntot-nsucc 个绿球，重量分别为 w1 和 w2. 从瓮中随机抽取 n 个球，拿到球的概率和它的重量成正比，而与其它球无关. 这种情况下，抽中蓝球的次数的分布可以由 Fisher 超几何分布模拟，其中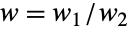， . 请注意该模型与定义 WalleniusHypergeometricDistribution 的瓮模型几乎一样，区别在于后者被非独立的抽取过程所模拟，而上述抽取过程中，每次抽取服从 BinomialDistribution 分布.
  • 可以用 Fisher 超几何分布对许多现实世界中的现象建模. 比如，模拟为有限食物资源竞争的物种的死亡情况（假定物种成员的命运彼此独立）. Fisher 超几何分布对蒙特卡罗仿真理论也很重要，可用来对列联表进行统计测试.
  • RandomVariate 可用来给出一个或更多机器精度或任意精度（后者可通过设置 WorkingPrecision 选项获得）的 Fisher 超几何分布中的伪随机变数. Distributed[x,FisherHypergeometricDistribution[n,nsucc,ntot,w]]，更简洁的式子为 xFisherHypergeometricDistribution[n,nsucc,ntot,w], 可用来声明随机变量 x 服从 Fisher 超几何分布. 它也可以被用在诸如 Probability、NProbability、Expectation 和 NExpectation 这样的函数中.
  • 通过使用 PDF[FisherHypergeometricDistribution[n,nsucc,ntot,w],x] 和 CDF[FisherHypergeometricDistribution[n,nsucc,ntot,w],x]，可以得到 Fisher 超几何分布的概率密度和累积分布函数. 可以用 Mean、Median、Variance、Moment 和 CentralMoment 来分别计算均值、中位数、方差、原始矩和中心矩. DiscretePlot 则可用来将这些量可视化.
  • 可以用 DistributionFitTest 来检测一个数据集是否符合 Fisher 超几何分布，根据给定数据，用 EstimatedDistribution 来估计参数化 Fisher 超几何分布，而 FindDistributionParameters 则可用来将数据拟合成 Fisher 超几何分布. 用 ProbabilityPlot 指令可以产生给定数据的 CDF 与符号式 Fisher 超几何分布的 CDF 的比较图，QuantilePlot 则能绘制给定数据的分位数和符号式 Fisher 超几何分布的分位数的比较图.
  • 可以用 TransformedDistribution 来表示转换过的 Fisher 超几何分布，用 CensoredDistribution 表示截尾后位于上限和下限值之间的数据的分布，而 TruncatedDistribution 则表示删失后位于上限和下限值之间的数据的分布. CopulaDistribution 可用来构建包含 Fisher 超几何分布的高维分布，ProductDistribution 可以计算包括独立分布为 Fisher 超几何分布所得的联合分布.
  • FisherHypergeometricDistribution 与许多其它分布有密切的关系. 如上所述，在 FisherHypergeometricDistribution、WalleniusHypergeometricDistribution 和 HypergeometricDistribution 之间有非常基本的联系. 考虑到 FisherHypergeometricDistribution[n,nsucc,ntot,1] 和 HypergeometricDistribution[n,nsucc,ntot] 的 PDF 一样，则后者之间的关系可以被定量精确描述. 此外，通过以两个服从 BinomialDistribution 的独立样本的和为条件， 可以得到FisherHypergeometricDistribution.

范例

打开所有单元关闭所有单元

基本范例  (3)

概率质量函数：

累积分布函数：

均值：

范围  (5)

产生一组服从超几何分布的伪随机数：

比较直方图和概率密度函数：

分布参数估计：

从样本数据估计分布参数：

比较样本的密度直方图和估计分布的概率密度函数：

以参数的函数形式表示不同矩的解析式：

Moment：

CentralMoment：

FactorialMoment：

符号阶数的解析式：

Cumulant：

风险函数：

分位数函数：

应用  (2)

FisherHypergeometricDistribution 的 CDF 是右连续函数的一个例子：

一个容器盛有重量为 的红球 个，以及重量为 的蓝球 个. 独立抽取 个球，抽到红球或蓝球的概率取决于它们的重量. 如果 ，，，，并且 ，求抽取的红球数目所服从的分布：

求至少抽取3个红球的概率：

求红球的平均数目：

模拟在样本数为12的30个连续样本中红球的数目：

属性和关系  (3)

与其它分布的关系：

HypergeometricDistribution 是一个特例：

FisherHypergeometricDistribution 可以从两个独立二项分布的变量得到，并以它们的和为条件：

Wolfram Research (2010)，FisherHypergeometricDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

文本

Wolfram Research (2010)，FisherHypergeometricDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

CMS

Wolfram 语言. 2010. "FisherHypergeometricDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html.

APA

Wolfram 语言. (2010). FisherHypergeometricDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_fisherhypergeometricdistribution, author="Wolfram Research", title="{FisherHypergeometricDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fisherhypergeometricdistribution, organization={Wolfram Research}, title={FisherHypergeometricDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/FisherHypergeometricDistribution.html}, note=[Accessed: 22-November-2024 ]}