FourierTransform

FourierTransform[expr,t,ω]

expr の記号フーリエ変換を与える．

FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}]

expr の多次元フーリエ変換を与える．

詳細とオプション

  • 関数 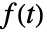のフーリエ変換はデフォルトでは 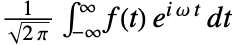で定義される．
  • 関数 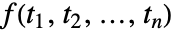の多次元フーリエ変換は，デフォルトで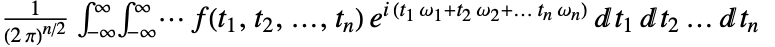，と定義される．
  • 理工学では他の定義が使用されることもある．
  • 別の定義はオプションFourierParametersを使用して指定できる．
  • FourierParameters->{a,b}と設定すると，FourierTransformで計算されるフーリエ変換は 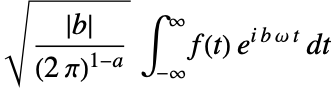となる．
  • よく使われる{a,b}の選択として，{0,1}（デフォルト，現代物理学），{1,-1} （純粋数学，システム工学），{-1,1}（古典物理学），{0,-2Pi}（信号処理）がある．
  • 次のオプションを与えることができる．
  • Assumptions $Assumptionsパラメータに関する仮定
    FourierParameters {0,1}フーリエ変換を定義するパラメータ
    GenerateConditions Falseパラメータに関す条件を含む解を生成するかどうか
  • FourierTransform[expr,t,ω]は，expr の記号フーリエ変換での連続変数 t に関する連続変数 ω に依存する式を出力する．Fourier[list]は有限個の数のリストの入力の離散フーリエ変換のリストを出力する．
  • TraditionalFormではFourierTransformは ℱを使用して出力される． »

例題

すべて開くすべて閉じる

例  (2)

スコープ  (6)

初等関数：

特殊関数：

区分関数と分布：

周期関数：

多変量関数：

TraditionalFormによる表示：

オプション  (3)

Assumptions  (1)

BesselJのフーリエ変換は区分関数である：

FourierParameters  (1)

デフォルト，現代物理学における規約：

純粋数学とシステム工学における規約：

古典物理学における規約：

信号処理における規約：

GenerateConditions  (1)

GenerateConditions->Trueを使って結果が有効になる場合のパラメータ的な条件を得る：

アプリケーション  (4)

減衰シヌソイドのパワースペクトル：

平面上の放射対称関数のフーリエ変換は，Hankel変換として表すことができる．以下で定義される関数についてこの関係を証明する：

関数をプロットする：

そのフーリエ変換を計算する：

HankelTransformを使って同じ結果を得る：

フーリエ変換をプロットする：

放射対称関数のリストについて，そのフーリエ変換の表を生成する：

これらの関数のHankel変換を計算する：

要求されたフーリエ変換の表を生成する：

定常OrnsteinUhlenbeckProcessのパワースペクトルを計算する：

特性と関係  (4)

Asymptoticを使って漸近近似を計算する：

FourierTransformとInverseFourierTransformは互いに逆関数である：

FourierTransformとFourierCosTransformは偶関数については等しい：

FourierTransformとFourierSinTransformは奇関数に関してはの分だけ異なる：

考えられる問題  (1)

逆フーリエ変換の結果はもとと同じ形であるとは限らない：

おもしろい例題  (1)

重みの付いたエルミート(Hermite)多項式のフーリエ変換は非常に簡単な形になる：

Wolfram Research (1999), FourierTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierTransform.html.

テキスト

Wolfram Research (1999), FourierTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierTransform.html.

CMS

Wolfram Language. 1999. "FourierTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierTransform.html.

APA

Wolfram Language. (1999). FourierTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierTransform.html

BibTeX

@misc{reference.wolfram_2024_fouriertransform, author="Wolfram Research", title="{FourierTransform}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/FourierTransform.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fouriertransform, organization={Wolfram Research}, title={FourierTransform}, year={1999}, url={https://reference.wolfram.com/language/ref/FourierTransform.html}, note=[Accessed: 25-November-2024 ]}