GaussianSymplecticMatrixDistribution
GaussianSymplecticMatrixDistribution[σ,n]
尺度母数 σ,行列次元{2 n,2 n}の複素平面上のガウス(Gauss)シンプレクティック行列分布を表す.
GaussianSymplecticMatrixDistribution[n]
単位尺度母数を持つガウスシンプレクティック行列分布を表す.
詳細

- GaussianSymplecticMatrixDistributionは,ガウスシンプレクティックアンサンブル(GSE)としても知られている.
- GaussianSymplecticMatrixDistributionは,シンプレクティックエルミート(Hermite)行列
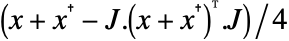 の分布である.ただし,
の分布である.ただし,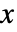 は,NormalDistribution[0,σ]に従う実部と虚部の行列要素を持つ,独立同分布に従う複素平方行列であり,
は,NormalDistribution[0,σ]に従う実部と虚部の行列要素を持つ,独立同分布に従う複素平方行列であり,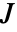 は歪対称行列KroneckerProduct[{{0,-1},{1,0}},IdentityMatrix[n]]である.
は歪対称行列KroneckerProduct[{{0,-1},{1,0}},IdentityMatrix[n]]である. - ガウスシンプレクティック行列分布中の四元数エルミート行列
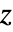 はブロック構造
はブロック構造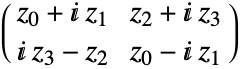 を持つ.ただし,
を持つ.ただし,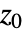 は行列次元{n,n}の対称実数行列で,
は行列次元{n,n}の対称実数行列で,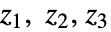 は行列次元{n,n}の反対称実数行列である.
は行列次元{n,n}の反対称実数行列である. 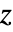 についての確率密度は
についての確率密度は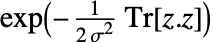 に比例する.
に比例する.- 尺度母数 σ は,任意の正の数でよく,次元母数 n は 任意の正の整数でよい.
- GaussianSymplecticMatrixDistributionは,MatrixPropertyDistribution,EstimatedDistribution,RandomVariate等の関数とともに使うことができる.
予備知識
- GaussianSymplecticMatrixDistribution[σ,n]は,ガウスシンプレクティックアンサンブル(GSE),とも呼ばれるもので,
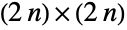 の複素シンプレクティックエルミート行列上の統計分布,具体的には
の複素シンプレクティックエルミート行列上の統計分布,具体的には 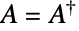 および
および 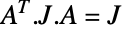 の両方を満足する偶数次元の複素行列
の両方を満足する偶数次元の複素行列 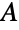 を表す.ただし,
を表す.ただし,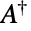 は
は 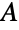 の共役転置,
の共役転置,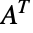 は
は 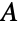 の転置,
の転置,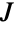 は
は 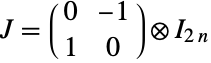 の形のシンプレクティック行列,⊗ はクロネッカー積を表す.GaussianSymplecticMatrixDistributionに従って分布する行列
の形のシンプレクティック行列,⊗ はクロネッカー積を表す.GaussianSymplecticMatrixDistributionに従って分布する行列 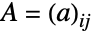 の確率密度は
の確率密度は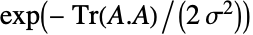 に比例する.さらに,すべての項の集合
に比例する.さらに,すべての項の集合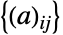 は,実部(Re)および虚部(Im)がNormalDistribution[0,σ]に従って一様に分布する複素変量の独立集合である.GaussianSymplecticMatrixDistribution[σ,n]は正の整数 n(次元母数)と正の実数 σ(尺度母数)によってパラメータ化される.「ガウスシンプレクティック行列分布」という名前ではあるが,この分布に属する行列がシンプレクティック行列である必要はない.
は,実部(Re)および虚部(Im)がNormalDistribution[0,σ]に従って一様に分布する複素変量の独立集合である.GaussianSymplecticMatrixDistribution[σ,n]は正の整数 n(次元母数)と正の実数 σ(尺度母数)によってパラメータ化される.「ガウスシンプレクティック行列分布」という名前ではあるが,この分布に属する行列がシンプレクティック行列である必要はない. - 母数が1つの形GaussianSymplecticMatrixDistribution[n]はGaussianSymplecticMatrixDistribution[1,n]に等しい.
- ガウスシンプレクティック行列分布は,ガウス直交アンサンブル(GaussianOrthogonalMatrixDistribution )およびガウスユニタリアンサンブル(GaussianUnitaryMatrixDistribution,)と並んで,Eugene Wignerによって原子物理学における揺らぎの研究のツールとして提唱された3つのガウス行列分布の一つである.ガウスシンプレクティックアンサンブルは,数学的にはシンプレクティック群の元による共役のもとで不変であり,物理的には回転対称性のない時間反転対称性でハミルトニアンをモデル化する.ガウスシンプレクティック行列分布のような行列アンサンブルは,ランダム行列理論をはじめとする物理学および数学のさまざま分野の研究において非常に重要である.
- RandomVariateを使って,ガウスシンプレクティック行列分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.そのような変量の集合の平均,中央値,分散,モーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.Distributed[A,GaussianSymplecticMatrixDistribution[σ,n]](より簡単な表記では AGaussianSymplecticMatrixDistribution[σ,n])を使ってランダム行列 A がガウスシンプレクティック行列分布に従って分布していると宣言することができる.そのような宣言はMatrixPropertyDistribution等の関数で使うことができる.
- ガウスシンプレクティック行列分布に従って分布する変量のトレース,固有値,ノルムは,それぞれTr,Eigenvalues,Normを使って計算することができる.そのような変量は,MatrixFunctionやMatrixPowerで調べることもできる.加えて,実部(Re),虚部(Im),複素引数(Arg) 等の関連する実際の量はMatrixPlotを使ってプロットできる.
- GaussianSymplecticMatrixDistributionは他の数多くの分布と関係がある.上述の通り,この分布は他のガウス行列分布と(GaussianOrthogonalMatrixDistributionおよびGaussianUnitaryMatrixDistribution)と定性的に類似している.ガウスアンサンブルの一般化には,いわゆる円行列アンサンブルが含まれるので,GaussianSymplecticMatrixDistributionはCircularOrthogonalMatrixDistribution,CircularQuaternionMatrixDistribution,CircularRealMatrixDistribution,CircularSymplecticMatrixDistribution,CircularUnitaryMatrixDistributionとも関係がある.GaussianSymplecticMatrixDistributionはMatrixNormalDistribution,MatrixTDistribution,WishartMatrixDistribution,InverseWishartMatrixDistribution,TracyWidomDistribution,WignerSemicircleDistributionとも関係がある.
例題
すべて開くすべて閉じる例 (3)
MatrixPropertyDistributionでランダム行列の固有値の結合分布を表し,そこからサンプルを取る:
スコープ (4)
アプリケーション (2)
ヒストグラムをDyson指数 ![]() についてのウィグナー(Wigner)推測としても知られる閉形式と比較する:
についてのウィグナー(Wigner)推測としても知られる閉形式と比較する:
RandomSampleを使ってランダムに固有値を置換し,アリゴリズム特有の順序を相殺する:
特性と関係 (4)
GaussianSymplecticMatrixDistributionの各実現はエルミート行列である:
さらに,GaussianSymplecticMatrixDistributionからのサンプル行列は四元数自己双対条件を満足する:
GaussianSymplecticMatrixDistributionからサンプルされた ![]() の
の ![]() に適用されたMatrixExpはユニタリシンプレクティック行列である:
に適用されたMatrixExpはユニタリシンプレクティック行列である:
大きいGSE行列のスペクトル密度はWignerSemicircleDistributionに収束する:
大きいGSE行列のスケールされた最大固有値の分布TracyWidomDistributionに収束する:
サンプルヒストグラムをTracyWidomDistribution[4]のPDFと比較する:
テキスト
Wolfram Research (2015), GaussianSymplecticMatrixDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html (2017年に更新).
CMS
Wolfram Language. 2015. "GaussianSymplecticMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html.
APA
Wolfram Language. (2015). GaussianSymplecticMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html