ImagePerspectiveTransformation[image,m]
applies a linear fractional transform specified by a matrix m to the positions of each pixel in image.
ImagePerspectiveTransformation[image,tf]
uses the TransformationFunction given by tf.
ImagePerspectiveTransformation[image,…,size]
gives an image of the specified size.
ImagePerspectiveTransformation[video,…]
transforms frames of a video.


ImagePerspectiveTransformation
ImagePerspectiveTransformation[image,m]
applies a linear fractional transform specified by a matrix m to the positions of each pixel in image.
ImagePerspectiveTransformation[image,tf]
uses the TransformationFunction given by tf.
ImagePerspectiveTransformation[image,…,size]
gives an image of the specified size.
ImagePerspectiveTransformation[video,…]
transforms frames of a video.
Details and Options
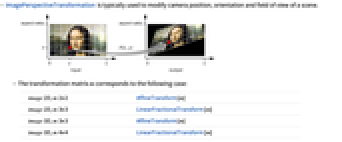


- ImagePerspectiveTransformation is typically used to modify camera position, orientation and field of view of a scene.
- The transformation matrix m corresponds to the following case:
-
image 2D, m 2×2 AffineTransform[m] image 2D, m 3×3 LinearFractionalTransform[m] image 3D, m 3×3 AffineTransform[m] image 3D, m 4×4 LinearFractionalTransform[m] - Possible settings for size are:
-
Automatic automatic image size All same as input image size width explicit width, automatic height {width,height} explicit width and height {width,depth,height} explicit width, depth and height in 3D - ImagePerspectiveTransformation can take the following options:
-
Background 0 background color to use DataRange Automatic range of coordinates in the original image Masking Full region of interest to be transformed Padding 0 padding method PlotRange Automatic range of coordinates in the resulting image Resampling Automatic resampling method - Typical settings for DataRange include:
-
Automatic 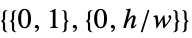 in 2D,
in 2D, 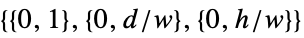 in 3D
in 3DFull 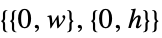 in 2D,
in 2D, 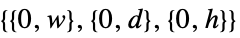 in 3D
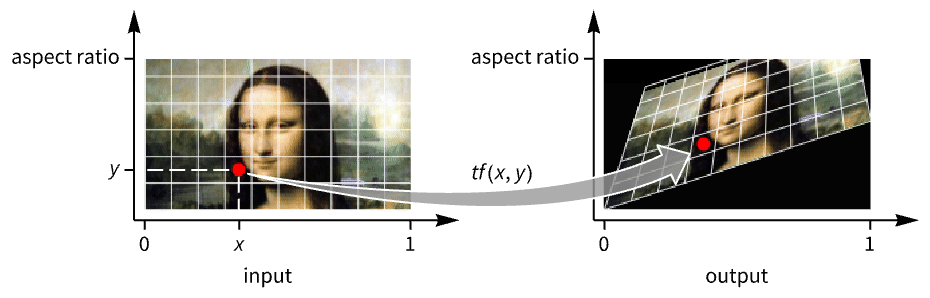
in 3D{{left,right},{bottom,top}} explicit coordinate ranges in 2D {{left,right},{front,back},{bottom,top}} explicit coordinate ranges in 3D - The coordinate system of the resulting image is specified by the PlotRange option. Typical settings include:
-
Automatic same as DataRange settings All try to include all of the transformed pixels Full same ranges as the input image {{left,right},…} explicit coordinate ranges - When PlotRange is not Automatic, size is chosen based on the size of the original image and the ratio of PlotRange and DataRange.
- Masking option can be one of the following:
-
All input image only Full input image and padding mask any mask image - For possible size specifications, see the reference page for ImageResize.
Examples
open all close allBasic Examples (2)
Scope (13)
Data (4)
Transformations (8)
2D Images (4)
A clockwise rotation of an image:
A general affine transformation:
Use a geometric transformation function to rotate an image:
Rotate about the opposite image corner:
Rotate about the image center:
Shear an image using ShearingTransform:
Transform an image using a general TransformationFunction object:
3D Images (4)
A pure rescaling of a 3D image:
Rotate a 3D image around the ![]() axis:
axis:
A pure translation of a 3D image in the vertical direction only:
Rotate a 3D image using RotationTransform:
Size (1)
The size value Automatic usually returns images of the same size as the original:
When PlotRange is specified, the returned image size is derived from the original size and plot range:
Using the value All always returns an image of the same size as the original:
Specify the width of the resulting image:
Options (7)
Background (1)
DataRange (2)
Masking (1)
Padding (1)
PlotRange (1)
Applications (4)
Use a perspective transformation to modify camera position in an image:
Obtain the geometric transformation that maps the four corners of the book to their desired positions:
Apply the transformation function to the image:
Remove the perspective distortion of the road:
Enhance the perspective effect:
Properties & Relations (2)
ImagePerspectiveTransformation[image,{a,b}] applies AffineTransform[{a,b}] to image:
ImagePerspectiveTransformation[image,{a,b,c,d}] applies LinearFractionalTransform[{a,b,c,d}] to image:
See Also
TransformationFunction FindGeometricTransform ImageForwardTransformation ImageTransformation AffineTransform
Function Repository: ImageShapeMorph
Related Guides
Text
Wolfram Research (2010), ImagePerspectiveTransformation, Wolfram Language function, https://reference.wolfram.com/language/ref/ImagePerspectiveTransformation.html (updated 2021).
CMS
Wolfram Language. 2010. "ImagePerspectiveTransformation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ImagePerspectiveTransformation.html.
APA
Wolfram Language. (2010). ImagePerspectiveTransformation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImagePerspectiveTransformation.html
BibTeX
@misc{reference.wolfram_2025_imageperspectivetransformation, author="Wolfram Research", title="{ImagePerspectiveTransformation}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ImagePerspectiveTransformation.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_imageperspectivetransformation, organization={Wolfram Research}, title={ImagePerspectiveTransformation}, year={2021}, url={https://reference.wolfram.com/language/ref/ImagePerspectiveTransformation.html}, note=[Accessed: 27-February-2026]}