InverseMellinTransform[expr,s,x]
expr の逆メリン変換を与える.


InverseMellinTransform
InverseMellinTransform[expr,s,x]
expr の逆メリン変換を与える.
詳細とオプション

- 関数
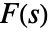 の逆メリン変換は
の逆メリン変換は 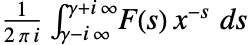
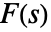 と定義され,関数
と定義され,関数 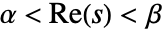 が正則となる
が正則となる 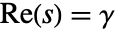 に存在する.場合によっては,この平面は半平面にまで拡張されることがある.
に存在する.場合によっては,この平面は半平面にまで拡張されることがある. - ConditionalExpression[expr,α<Re[s]<β]を使って正則部分を示すことができる. »
- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータの条件を含む結果を生成するかどうか Method Automatic 使用するメソッド - GenerateConditionsを使って正則部分を得ることができる. »
- Assumptionsを使って正則部分を指定することができる. »
- AssumptionsとConditionalExpressionの両方を使って正則部分に制限が加えられた場合は,両部分の共通集合が使われる.
- TraditionalFormでは,InverseMellinTransformは
![TemplateBox[{{F, (, s, )}, s, x}, InverseMellinTransform1] TemplateBox[{{F, (, s, )}, s, x}, InverseMellinTransform1]](Files/InverseMellinTransform.ja/7.png) を使って出力される.
を使って出力される.
例題
すべて開く すべて閉じる例 (2)
スコープ (10)
基本的な用法 (4)
InverseMellinTransformが仮定する正則部分を得る:
TraditionalForm による表示:
オプション (2)
Assumptions (1)
この例でInverseMellinTransformが返す答はRe[s]>0について有効である:
Assumptionsを使って別の正則部分を指定する:
ConditionalExpressionを使って同じ仮定を指定する:
GenerateConditions (1)
InverseMellinTransformの結果の信頼性についての条件を得る:
GenerateConditionsはこの例ではデフォルトでFalseに設定されている:
アプリケーション (2)
![]() を評価する.これは次の関数のメリンたたみ込みとみなすことができる:
を評価する.これは次の関数のメリンたたみ込みとみなすことができる:
各関数にMellinTransformを適用する:
Integrateを使って直接積分を計算する:
MellinConvolveを使って同じ結果を得る:
メリン変換のテクニックを使って微分方程式についての特定の解を求める:
MellinTransformを方程式に適用する:
InverseMellinTransformを使って必要な解を計算する:
DSolveValueを無限大における境界条件とともに使って解を得る:
特性と関係 (4)
Asymptoticを使って漸近近似を計算する:
InverseMellinTransformとMellinTransformは互いに逆関数である:
InverseMellinTransformは線形演算子である:
考えられる問題 (2)
InverseMellinTransformは,仮定によって異なる結果を返すことがある:
関連するガイド
-
▪
- 積分変換
テキスト
Wolfram Research (2016), InverseMellinTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseMellinTransform.html.
CMS
Wolfram Language. 2016. "InverseMellinTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseMellinTransform.html.
APA
Wolfram Language. (2016). InverseMellinTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseMellinTransform.html
BibTeX
@misc{reference.wolfram_2025_inversemellintransform, author="Wolfram Research", title="{InverseMellinTransform}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InverseMellinTransform.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_inversemellintransform, organization={Wolfram Research}, title={InverseMellinTransform}, year={2016}, url={https://reference.wolfram.com/language/ref/InverseMellinTransform.html}, note=[Accessed: 11-March-2026]}