InverseTransformedRegion[reg,f,n]
represents the inverse transformed region ![]() , where reg is a region and f is a function.
, where reg is a region and f is a function.


InverseTransformedRegion
InverseTransformedRegion[reg,f,n]
represents the inverse transformed region ![]() , where reg is a region and f is a function.
, where reg is a region and f is a function.
Details and Options
- InverseTransformedRegion is also known as the inverse image or preimage of a region.
- InverseTransformedRegion[reg,f] is equivalent to InverseTransformedRegion[reg,f,RegionEmbeddingDimension[reg]].
Examples
open all close allBasic Examples (2)
Scope (22)
Special Regions (9)
Some inverse transformed regions are computed explicitly:
The inverse image of the unit cuboid through a linear-fractional transformation:
The inverse transform of a translated unit Disk:
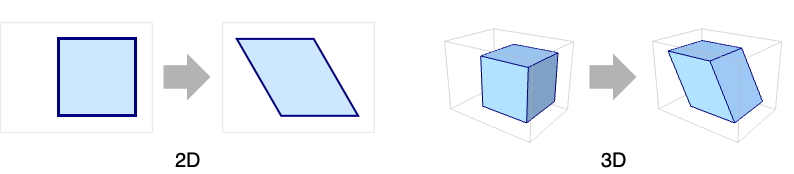
The inverse transform of a sheared unit Rectangle:
The inverse transform of a rotated Triangle:
The inverse transform of a scaled Circle:
The inverse image of the unit cube through a rotation transform:
An inverse transform of a rectangle by a linear transformation ![]() :
:
Map points from a Triangle embedded in 2D into 3D by a nonlinear transformation ![]() :
:
Formula Regions (4)
The inverse transform of a sheared ParametricRegion:
The inverse transform of a rotated ParametricRegion:
The inverse transform of a sheared ImplicitRegion:
The inverse transform of a scaled ImplicitRegion:
Mesh Regions (2)
An inverse transform of BoundaryMeshRegion objects is a BoundaryMeshRegion:
An inverse transform of MeshRegion objects is a MeshRegion:
Derived Regions (5)
The inverse transform of a reflected TransformedRegion:
The inverse transform of a rotated RegionDifference:
The inverse transform of a scaled RegionBoundary:
The inverse transform of a reflected RegionProduct:
The inverse transform of a RegionUnion by a nonlinear transformation ![]() :
:
Geographic Regions (2)
InverseTransformedRegion works on polygons of geographic entities:
Polygons with GeoPosition:
Polygons with GeoGridPosition:
Related Guides
History
Text
Wolfram Research (2014), InverseTransformedRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseTransformedRegion.html.
CMS
Wolfram Language. 2014. "InverseTransformedRegion." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseTransformedRegion.html.
APA
Wolfram Language. (2014). InverseTransformedRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseTransformedRegion.html
BibTeX
@misc{reference.wolfram_2025_inversetransformedregion, author="Wolfram Research", title="{InverseTransformedRegion}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/InverseTransformedRegion.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_inversetransformedregion, organization={Wolfram Research}, title={InverseTransformedRegion}, year={2014}, url={https://reference.wolfram.com/language/ref/InverseTransformedRegion.html}, note=[Accessed: 05-March-2026]}