JohnsonDistribution["SB",γ,δ,μ,σ]
represents a bounded Johnson distribution with shape parameters γ, δ, location parameter μ, and scale parameter σ.
JohnsonDistribution["SL",γ,δ,μ,σ]
represents a semi-bounded Johnson distribution.
JohnsonDistribution["SU",γ,δ,μ,σ]
represents an unbounded Johnson distribution.
JohnsonDistribution["SN",γ,δ,μ,σ]
represents a normal Johnson distribution.


JohnsonDistribution
JohnsonDistribution["SB",γ,δ,μ,σ]
represents a bounded Johnson distribution with shape parameters γ, δ, location parameter μ, and scale parameter σ.
JohnsonDistribution["SL",γ,δ,μ,σ]
represents a semi-bounded Johnson distribution.
JohnsonDistribution["SU",γ,δ,μ,σ]
represents an unbounded Johnson distribution.
JohnsonDistribution["SN",γ,δ,μ,σ]
represents a normal Johnson distribution.
Details

- JohnsonDistribution represents the Johnson system of distributions. Each distribution represents the distribution of the form
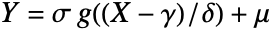 , where
, where 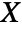 is from NormalDistribution[].
is from NormalDistribution[]. - JohnsonDistribution["SB",γ,δ,μ,σ] corresponds to
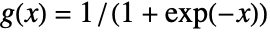 .
. - JohnsonDistribution["SL",γ,δ,μ,σ] corresponds to
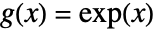 .
. - JohnsonDistribution["SU",γ,δ,μ,σ] corresponds to
 .
. - JohnsonDistribution["SN",γ,δ,μ,σ] corresponds to
 .
. - JohnsonDistribution allows γ and μ to be any real numbers and δ and σ to be any positive real numbers.
- JohnsonDistribution allows μ and σ to be any quantities of the same unit dimensions, and δ, γ to be dimensionless quantities. »
- JohnsonDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- JohnsonDistribution["type",γ,δ,μ,σ] represents a statistical distribution belonging to one of four types as determined by its first argument and parametrized by real numbers γ (called a "shape parameter") and μ (called a "location parameter") and positive real numbers δ (called a "shape parameter") and σ (called a "scale parameter"). Overall, the probability density function (PDF) of a Johnson distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and its concentration near the
 axis) is completely determined by the values of its arguments. In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than decreasing algebraically for large values of x. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
axis) is completely determined by the values of its arguments. In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than decreasing algebraically for large values of x. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Johnson distributions originate with English statistician Norman Johnson, who devised them in the late 1940s in order to apply the well-established methods and theory of the normal distribution (NormalDistribution) to a wide range of possibly non-normal probability distributions via a series of simple transformations that are all easily computable using function tables that existed at the time. In particular, given an observed distribution which is non-normal, the exponential, logistic, and hyperbolic sine transformations generate Johnson distributions of which are log-normal (of type "SL"), unbounded ("SU"), and bounded ("SB") distributions, respectively; the normal ("SN") distribution corresponds to an observed distribution that is already normally distributed. Because of its flexibility, the family of Johnson distributions has been used to analyze real-world datasets in various fields including atmospheric chemistry, biomedical engineering, econometrics, management, and material science.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Johnson distribution. Distributed[x,JohnsonDistribution["type",γ,δ,μ,σ]], written more concisely as xJohnsonDistribution["type",γ,δ,μ,σ], can be used to assert that a random variable x is distributed according to a Johnson distribution of a given "type" (one of "SB", "SL", "SN", or "SU" as discussed above). Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Johnson distributions may be given using PDF[JohnsonDistribution["type",γ,δ,μ,σ],x] and CDF[JohnsonDistribution["type",γ,δ,μ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Johnson distribution, EstimatedDistribution to estimate a Johnson parametric distribution from given data, and FindDistributionParameters to fit data to a Johnson distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Johnson distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Johnson distribution.
- TransformedDistribution can be used to represent a transformed Johnson distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Johnson distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Johnson distributions.
- JohnsonDistribution is closely related to a number of other distributions. For example, JohnsonDistribution was compared to and contrasted with PearsonDistribution in Johnson's original paper, and the distributions were defined in such a way that all four types are transformations (via TransformedDistribution) of NormalDistribution. The "SL" type JohnsonDistribution is a generalization of LogNormalDistribution, and JohnsonDistribution is also closely related to HalfNormalDistribution, FisherZDistribution, ArcSinDistribution, BetaPrimeDistribution, PowerDistribution, ParetoDistribution, InverseChiSquareDistribution, and ErlangDistribution.
Examples
open all close allBasic Examples (5)
Scope (8)
Generate a sample of pseudorandom numbers from a bounded Johnson distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Skewness for semi-bounded (SL):
Kurtosis for semi-bounded (SL):
Different moments with closed forms as functions of parameters:
Bounded (SB), no closed formula for symbolic parameters, but can be evaluated numerically:
Hazard function for bounded (SB):
Quantile function for bounded (SB):
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Properties & Relations (8)
The Johnson distribution family is closed under translation and scaling by a positive factor:
Relations to other distributions:
Normal (SN) Johnson distribution is a NormalDistribution:
Normal (SN) Johnson distribution is a transformation of standard NormalDistribution:
Semi-bounded (SL) Johnson distribution as a transformation of NormalDistribution:
Unbounded (SU) Johnson distribution as a transformation of NormalDistribution:
Bounded (SB) Johnson distribution as a transformation of a NormalDistribution:
Special case of SL Johnson distribution is a LogNormalDistribution:
Related Guides
Text
Wolfram Research (2010), JohnsonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/JohnsonDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "JohnsonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/JohnsonDistribution.html.
APA
Wolfram Language. (2010). JohnsonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JohnsonDistribution.html
BibTeX
@misc{reference.wolfram_2025_johnsondistribution, author="Wolfram Research", title="{JohnsonDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/JohnsonDistribution.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_johnsondistribution, organization={Wolfram Research}, title={JohnsonDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/JohnsonDistribution.html}, note=[Accessed: 03-March-2026]}