LindleyDistribution
形状母数 δ のLindley分布を表す.
詳細
- 値
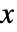 の確率密度は
の確率密度は 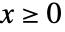 では
では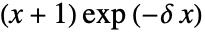 に比例し,
に比例し,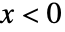 では0である.
では0である. - LindleyDistribution では,δ は任意の正の実数でよい.
- LindleyDistributionでは,δ は無次元量でよい. »
- LindleyDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- LindleyDistribution[δ]は,区間
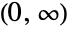 上でサポートされ,自身の確率密度関数(PDF)の全体的な動作を決定する正の実数 δ(「形状母数」と呼ばれる)でパラメータ化された統計分布を表す.Lindley分布の形は,母数 δ によって,単一の「峰」(最大値)を持つ単峰性か,潜在的特異値が領域の下限境界に近付く単調減少かのどちらかになる.これに加え,PDFの裾部は,
上でサポートされ,自身の確率密度関数(PDF)の全体的な動作を決定する正の実数 δ(「形状母数」と呼ばれる)でパラメータ化された統計分布を表す.Lindley分布の形は,母数 δ によって,単一の「峰」(最大値)を持つ単峰性か,潜在的特異値が領域の下限境界に近付く単調減少かのどちらかになる.これに加え,PDFの裾部は,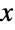 の大きい値についてPDFが代数的にではなくむしろ指数的に減少するという意味で「細い
の大きい値についてPDFが代数的にではなくむしろ指数的に減少するという意味で「細い
」(この動作は分布のSurvivalFunctionを分析することで数量的に正確にすることができる).専門家たちはLindley分布が指数分布(ExponentialDistribution)と数量的に類似していることに気付いた.「Lindley–Exponential分布」という用語はLindley分布の一般化に使われることもあるが,Lindley分布と指数分布は別の分布だということに留意する必要がある. - Lindley分布は英国の統計学者であるD. V. Lindleyによって開発され,1958年に発表された論文で,ベイズ理論と相対的ないわゆるフィデューシャル分布(既知の分布の正確に「逆」の分布)の大きい理論的研究の例として発表された.この分布の特性自体は2008年のGhitany et alによる論文まで比較的研究されずに来たが,例えそうでも,Lindley分布は顧客の待ち時間のような現実世界のデータのモデル化に使用されてきており,癌患者の生存率,ストレス度,信頼度統計,植物の葉に保たれている炭素,その他多くの寿命データをモデル化するために一般化されてきている.
- RandomVariateを使って,Lindley分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,LindleyDistribution[δ]](より簡略な表記では xLindleyDistribution[δ])を使って,確率変数 x がLindley分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[LindleyDistribution[δ],x]およびCDF[LindleyDistribution[δ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がLindley分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックLindley分布を推定することが,FindDistributionParametersを使ってデータをLindley分布にフィットすることができる.ProbabilityPlotを使って記号Lindley分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Lindley分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたLindley分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってLindley分布を含む高次元分布を構築することが,ProductDistributionを使ってLindley分布を含む独立成分分布の結合分布を計算することができる.
- LindleyDistributionは,上述のExponentialDistributionとの品質類似性を含み,他の数多くの分布と関連している.さらに,Ghitany et al.は,LindleyDistribution[δ]のPDF
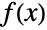 がExponentialDistribution[δ]とGammaDistribution[2,δ]の線形結合として書けるという意味で,LindleyDistributionがExponentialDistributionとGammaDistributionの特殊な混合として書けることを示した.加えて,LindleyDistributionは,PoissonDistribution,BetaDistribution,ExponentialDistribution,PowerDistributionを含む多くのよく知られた分布と数量的特性を共有するように一般化されている.
がExponentialDistribution[δ]とGammaDistribution[2,δ]の線形結合として書けるという意味で,LindleyDistributionがExponentialDistributionとGammaDistributionの特殊な混合として書けることを示した.加えて,LindleyDistributionは,PoissonDistribution,BetaDistribution,ExponentialDistribution,PowerDistributionを含む多くのよく知られた分布と数量的特性を共有するように一般化されている.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元のQuantityを使ってLindleyDistributionを定義する:
アプリケーション (2)
LindleyDistributionを使って離散Poisson–Lindley分布を作成することができる:
平均はLindleyDistributionのそれと等しい:
Poisson–Lindley分布を使って保険金の支払い請求数をモデル化することができる:
PoissonDistributionのみを使ったときよりもよりよくフィットする:
テキスト
Wolfram Research (2010), LindleyDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/LindleyDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "LindleyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LindleyDistribution.html.
APA
Wolfram Language. (2010). LindleyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LindleyDistribution.html