MaxwellDistribution
尺度母数が σ のマクスウェル(Maxwell)分布を表す.
詳細
- MaxwellDistributionはMaxwell–Boltzmann分布としても知られている.
- マクスウェル分布における値
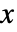 の確率密度は,
の確率密度は,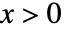 のときは
のときは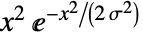 に比例し,
に比例し,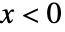 のときは0である. »
のときは0である. » - MaxwellDistributionでは,σ は任意の正の実数でよい.
- MaxwellDistributionでは,σ は任意の単位次元の数量でよい. »
- MaxwellDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- MaxwellDistribution[σ]は,区間
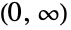 上でサポートされ,その確率密度関数(PDF)の全体的な動作を決定する正の実数 σ(「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.一般に,マクスウェル分布のPDFは単一の「峰」(大域的最大値)を持つ単峰性であるが,その全体的な形(高さ,広がり,最大値の水平位置)は σ の値で決定される.加えて,マクスウェル分布のPDFの裾部はPDFが
上でサポートされ,その確率密度関数(PDF)の全体的な動作を決定する正の実数 σ(「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.一般に,マクスウェル分布のPDFは単一の「峰」(大域的最大値)を持つ単峰性であるが,その全体的な形(高さ,広がり,最大値の水平位置)は σ の値で決定される.加えて,マクスウェル分布のPDFの裾部はPDFが 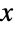 の大きい値について代数的というよりもむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunctionを分析することで数量的に厳密にすることができる).マクスウェル分布は,Maxwell-Boltzmann分布あるいはマクスウェル速度分布と呼ばれることもある.
の大きい値について代数的というよりもむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunctionを分析することで数量的に厳密にすることができる).マクスウェル分布は,Maxwell-Boltzmann分布あるいはマクスウェル速度分布と呼ばれることもある. - マクスウェル分布は1860年代にスコットランド人の物理学者であるJames Clark Maxwellによって初めて説明された.この分布は,のちにオーストリア人の物理学者であるLudwig Boltzmannによる研究によって,統計力学における不可欠なモデルになった.マクスウェル分布は,粒子が熱力学的平衡に到達し互いの干渉が最小限であるという仮定のもとで,理想気体中の粒子速度を説明する.このため,この分布は気体の動力学理論の根本であるとみなされており,より一般的なレベルにおける非干渉粒子の分布を説明しようとする関連分野のMaxwell-Boltzmann統計におけるツールになっている.この分布は,化学,信頼性とリスクの解析,信号処理,ベイズ解析を含むさまざまな分野における現象の説明にも使われている.
- RandomVariateを使って,マクスウェル分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,MaxwellDistribution[σ]](より簡略な表記では xMaxwellDistribution[σ])を使って,確率変数 x がマクスウェル分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[MaxwellDistribution[σ],x]およびCDF[MaxwellDistribution[σ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がマクスウェル分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックマクスウェル分布を推定することが,FindDistributionParametersを使ってデータをマクスウェル分布にフィットすることができる.ProbabilityPlotを使って記号マクスウェル分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号マクスウェル分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたマクスウェル分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってマクスウェル分布を含む高次元分布を構築することが,ProductDistributionを使ってマクスウェル分布を含む独立成分分布の結合分布を計算することができる.
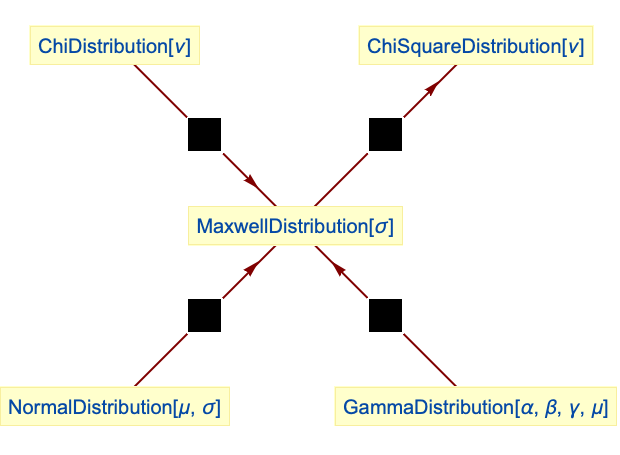
- MaxwellDistributionは他の数多くの分布と関連して知る.この分布はChiDistribution(MaxwellDistribution[1]のPDFはChiDistribution[3]のそれと厳密に等しい),ChiSquareDistribution(CDF[MaxwellDistribution[1],Sqrt[x]]はCDF[ChiSquareDistribution[3],x]に等しい),GammaDistribution(MaxwellDistribution[σ]とGammaDistribution[3/2,Sqrt[2] σ,2,0]のPDFは等しい)の特殊ケースである.MaxwellDistributionは,指数関数的減衰動作のために,NormalDistribution,RayleighDistribution,BetaDistribution,ExponentialDistributionと数量的に類似している.MaxwellDistributionはChiDistributionおよびChiSquareDistributionとの関係を通してNakagamiDistribution,NoncentralChiSquareDistribution,HalfNormalDistributionとも関連している.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantity を一貫して使うとQuantityDistributionが与えられる:
アプリケーション (2)
特性と関係 (7)
マクスウェル分布は正の因子によるスケーリングの下では閉じている:
![]() のMaxwellDistributionはChiDistributionの特殊ケースである:
のMaxwellDistributionはChiDistributionの特殊ケースである:
![]() のMaxwellDistributionの平方はChiSquareDistributionの特殊ケースである:
のMaxwellDistributionの平方はChiSquareDistributionの特殊ケースである:
MaxwellDistributionはGammaDistributionの特殊ケースである:
考えられる問題 (2)
テキスト
Wolfram Research (2007), MaxwellDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MaxwellDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "MaxwellDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MaxwellDistribution.html.
APA
Wolfram Language. (2007). MaxwellDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaxwellDistribution.html