Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

NSurfaceIntegrate

NSurfaceIntegrate[f,{x,y,…}∈surface]

计算函数 f[x,y,…] 在 surface 上的数值标量曲面积分.

NSurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

计算向量场 {p[x,y,…],q[x,y,…],…} 的数值向量曲面积分.

更多信息和选项

曲面积分亦称为通量积分.
标量曲面积分在超曲面上对标量函数进行积分. 它们通常用于计算曲面的面积、质量和电荷等.
向量曲面积分用于计算向量函数沿其法线方向通过曲面的通量. 典型的向量函数包括流体速度场、电场和磁场.
函数 f 在 surface 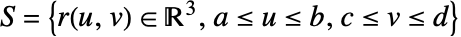上的标量曲面积分由下式给出：

… 其中 $TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm]$ 是参数化曲面元素的度量.
f 在超曲面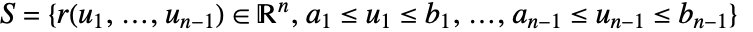上的标量曲面积分由下式给出：

标量曲面积分与 surface 的参数化和方向无关. 任何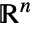中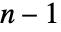维的 RegionQ 对象都可以用作 surface.
向量函数在 surface 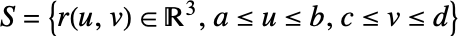上的向量曲面积分由下式给出：

… 其中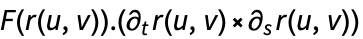是向量函数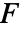在法线方向上的投影，因此只对法线方向上的分量进行积分.
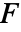在超曲面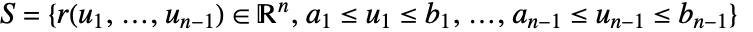上的向量曲面积分由下式给出：

向量曲面积分与参数化无关，但与方向有关.
超曲面的方向由曲面上的法向向量场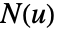给出.

对于参数化超曲面 ParametricRegion[{r₁[u₁,…,u_n-1],…,r_n[u₁,…,u_n-1]},…]，法向向量场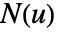为 Cross[∂_u₁r[u],…,∂_{u_n-1}r[u]].
Wolfram 语言中的 RegionQ 对象是没有方向的. 但是，为了方便使用此函数，可以假设以下规则来获取有方向的超曲面.
对于（维度为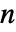的）实体和有界的 RegionQ 对象 ℛ，将曲面视为区域的边界 (RegionBoundary[ℛ])，且法线方向指向外侧.
中的特殊实体及认定的边界曲面（边）的法线方向包括：

		Triangle	外向法线
		Rectangle	外向法线
		Polygon	外向法线
		Disk	外向法线
		Ellipsoid	外向法线
		Annulus	外向法线

中的特殊实体及认定的边界曲面（面）的法线方向包括：

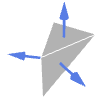
		Tetrahedron	外向法线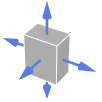
		Cuboid	外向法线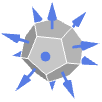
		Polyhedron	外向法线
		Ball	外向法线
		Ellipsoid	外向法线
		Cylinder	外向法线
		Cone	外向法线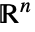

中的特殊实体及认定的表面（面）和法线方向包括：
Simplex 外向法线

Cuboid 外向法线

Ball 外向法线

Ellipsoid 外向法线
可给出以下选项：

	AccuracyGoal	Automatic	寻求的绝对准确度
	MaxPoints	Automatic	样本点的最大数量
	MaxRecursion	Automatic	递归子划分的最大数量
	Method	Automatic	要使用的方法
	MinRecursion	0	递归子划分的最小数量
	PrecisionGoal	Automatic	寻求的精度
	WorkingPrecision	Automatic	内部计算使用的精度

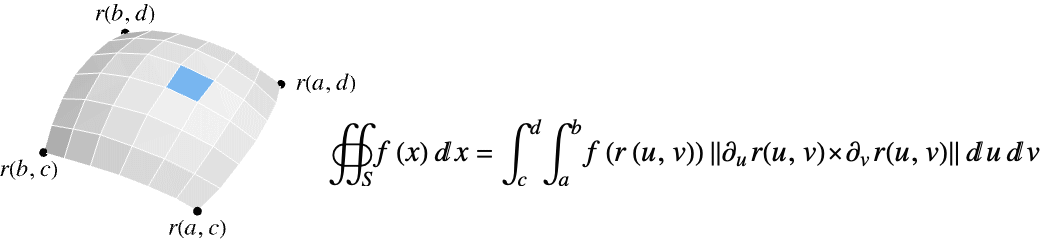
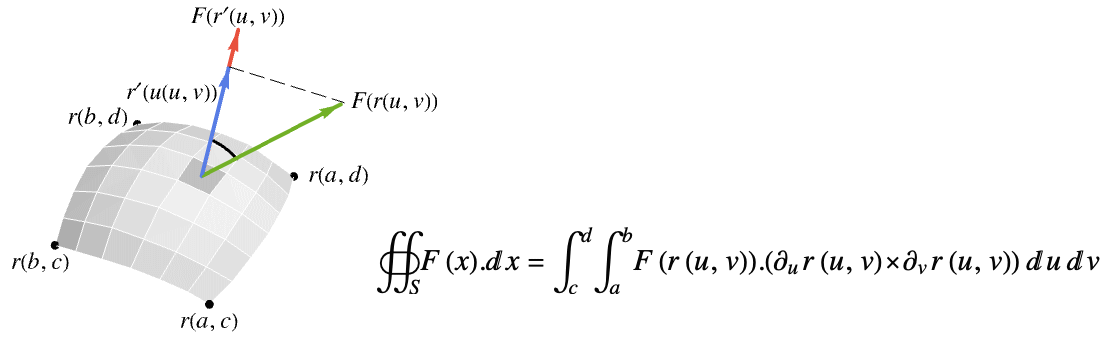
范例

打开所有单元关闭所有单元

基本范例 (6)

标量函数在球面上的曲面积分：

向量场在球面上的曲面积分：

标量场在参数化曲面上的曲面积分：

向量场在参数化曲面上的曲面积分：

标量场在曲面上的曲面积分：

可视化曲面上的标量场：

向量场在曲面上的曲面积分：

可视化曲面上的向量场：

范围 (32)

基本用法 (5)

标量场在三维立方体上的曲面积分：

向量场在三维空间的曲面积分：

SurfaceIntegrate 适用于许多特殊曲面：

参数化曲面上的曲面积分：

SurfaceIntegrate 还适用于其他维度：

标量函数 (5)

标量场在三维曲面上的曲面积分：

曲面图：

曲面积分：

标量场在三角形上的曲面积分：

曲面积分：

标量场在三维球面上的曲面积分：

标量场在金字塔表面上的曲面积分：

曲面积分：

标量场在三维参数化曲面上的曲面积分：

曲面及绘图：

向量函数 (5)

向量场在三维球面上的曲面积分：

可视化球面上的向量场：

曲面积分：

三维空间中向量场在三角形上的曲面积分：

曲面积分：

向量场在三维参数化曲面上的曲面积分：

向量场在椭球边界上的曲面积分：

三维空间中向量场在圆锥边界上的曲面积分：

曲面上向量场的可视化：

曲面积分：

特殊曲面 (10)

向量场在半径为 1 的球面上的曲面积分：

向量场在以原点为中心、边长为 2 的立方体边界上的曲面积分：

向量场在四面体边界上的曲面积分：

向量场在三角形上的曲面积分：

向量场在椭球上的曲面积分：

向量场在圆锥边界上的曲面积分：

向量场在圆柱边界上的曲面积分：

向量场在平行六面体边界上的曲面积分：

向量场在棱柱边界上的曲面积分：

三维多边形上的曲面积分：

多边形的方向取决于给出点的顺序：

参数化曲面 (4)

向量场在参数化曲面上的曲面积分：

向量场在参数化圆顶状曲面上的曲面积分：

参数化圆柱上的曲面积分：

向量场在参数化双曲面上的曲面积分：

超曲面 (3)

2D 中 1D 超曲面上的曲面积分：

4D 中 3D 超曲面上的曲面积分：

五维球面的体积，使用曲面积分计算：

选项 (8)

AccuracyGoal (1)

选项 AccuracyGoal 设置准确度的位数：

默认设置仅设定 PrecisionGoal：

MaxPoints (1)

选项 MaxPoints 在计算指定数量的点后停止积分：

使用默认选项：

MaxRecursion (1)

选项 MaxRecursion 指定最大递归步骤数：

增大递归计算的次数：

Method (1)

选项 Method 可接受与 NIntegrate 同样的值. 例如：

使用默认选项：

MinRecursion (1)

对于具有尖锐峰值的函数，选项 MinRecursion 强制使用最小数量的递归子划分：

与精确结果进行比较：

PrecisionGoal (1)

选项 PrecisionGoal 设置积分中的相对容差：

使用默认设置：

WorkingPrecision (2)

如果指定了 WorkingPrecision，则以该工作精度完成计算：

被积函数的精度可能有限：

应用 (18)

大学微积分 (5)

以原点为中心、边长为 2 的立方体边界上的曲面积分：

抛物面上的曲面积分：

圆柱体表面上的曲面积分：

半径为 2 的半球壳上的曲面积分：

立方体边界上的曲面积分：

面积 (3)

球面的面积：

椭球的面积：

三角形的面积：

体积 (3)

用曲面积分计算椭球的体积：

用曲面积分计算二十面体的体积：

用曲面积分计算边长为 3 的立方体的体积：

通量 (3)

原点处的点电荷在包围它的的球面上产生的电场通量：

每单位长度有个绕组的无限螺线管的均匀磁场通量，电流在与其正交的圆盘上穿过：

线电荷密度为的无限带电导线产生的电场：

穿过高度为、半径为、轴位于带电导线上的圆柱的电通量：

质心 (2)

具有单位密度和半径的半球壳的质量：

质心的坐标：

质心的坐标：

质心的坐标：:

薄切圆锥体的惯性矩：

关于轴：

关于轴：

关于轴：

经典定理 (2)

斯托克斯定理. 向量场的 Curl，即的曲面积分：

在开放曲面上的曲面积分为：

与在曲面边界上的线积分相同：

散度定理. 向量场（具有连续偏导数）在闭合曲面上的曲面积分为：

与 Div[f] 在曲面内部的积分相同：

属性和关系 (5)

如果符号计算失败，可用 N[SurfaceIntegrate[…]] 通过 NSurfaceIntegrate 获得数值解：

求单位面积单位质量的薄三角形曲面的质心：

求总质量：

求质心的分量：

求质心的分量：

求质心的分量：

也可以用 RegionCentroid 求得质心：

求单位面积密度的薄圆柱壳绕轴的惯性矩：

也可用 MomentOfInertia 获得答案：

求四面体的面积：

也可用 SurfaceArea 获得答案：

求二十面体的体积：

也可用 Volume 获得答案：

巧妙范例 (9)

用曲面积分计算的伪球体的体积：

伪球面有限部分的绘图：

用曲面积分计算水滴形固体的体积：

Dupin cyclide 的体积：

穿过部分波西米亚圆顶的向量场的通量：

向量场在部分 conocuneus of Wallis 上的曲面积分：

向量场在漏斗形曲面上的曲面积分：

Gaudi 曲面的面积：

用数值法计算 Guimard 曲面的面积：

向量场在 Neiloid 上的曲面积分：

顶部