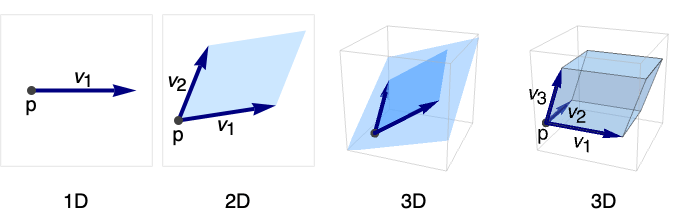
Parallelepiped
Parallelepiped[p,{v1,…,vk}]
represents a parallelepiped with origin p and directions vi.
Details and Options

- Parallelepiped is also known as parallelogram, rhombohedron, and parallelotope.
- Parallelepiped represents
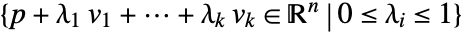 , where the vectors vi have to be linearly independent.
, where the vectors vi have to be linearly independent. - Parallelepiped can be used as a geometric region and graphics primitive.
- Parallelepiped can be used in Graphics and Graphics3D.
- In graphics, the point p and vectors vi can be Scaled and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, and color.
Examples
open allclose allBasic Examples (3)
A Parallelepiped in 3D:
Scope (16)
Graphics (6)
Specification (2)
Styling (2)
Regions (10)
Embedding dimension is the dimension of the space in which the parallelepiped lives:
Geometric dimension is the dimension of the shape itself:
Compute a bounding box for the region:
Integrate over a Parallelepiped:
Solve equations over a Parallelepiped:
Applications (3)
For a full-dimensional Parallelepiped, the measure is easily computed from the vectors:
The volume is equal to the absolute value of the determinant of the matrix ![]() :
:
For a lower-dimensional Parallelepiped, the square root of the Gram determinant is used:
The Gram determinant is the determinant of ![]() dotted with its Transpose:
dotted with its Transpose:
Any full-dimensional Parallelepiped can tile space:
Properties & Relations (5)
Parallelogram is the 2D full-dimensional case of Parallelepiped:
Rectangle is a 2D Parallelepiped with axis-aligned edges:
Cuboid is a 3D Parallelepiped with axis-aligned edges:
Any Parallelepiped is an AffineTransform of a Cuboid:
Hexahedron is a generalization of a 3D Parallelepiped:
Text
Wolfram Research (2014), Parallelepiped, Wolfram Language function, https://reference.wolfram.com/language/ref/Parallelepiped.html.
CMS
Wolfram Language. 2014. "Parallelepiped." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Parallelepiped.html.
APA
Wolfram Language. (2014). Parallelepiped. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Parallelepiped.html