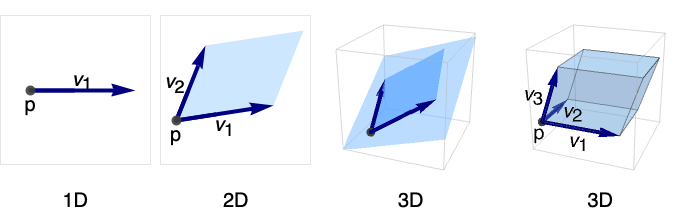
Parallelepiped

Parallelepiped[p,{v1,…,vk}]

原点 p，方向 viの平行六面体を表す．

詳細とオプション

  • Parallelepipedは，平行四辺形，斜方六面体，平行体としても知られている．
  • Parallelepipedは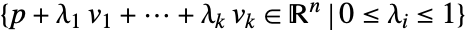を表す．ただし，ベクトル viは線形独立でなければならない．
  • Parallelepipedは，幾何学領域およびグラフィックスプリミティブとして使われる．
  • ParallelepipedはGraphicsおよびGraphics3Dで用いることができる．
  • グラフィックスでは，点 p およびベクトル viは，Scaled式およびDynamic式でもよい．
  • グラフィックスの描画は，FaceForm，EdgeForm，Opacity，色等の指示子の影響を受ける．

例題

すべて開くすべて閉じる

例  (3)

3DにおけるParallelepiped：

2Dにおけるもの：

さまざまなスタイルを適用された平行六面体：

体積と重心：

スコープ  (16)

グラフィックス  (6)

指定  (2)

次元の平行六面体は基底点と 個までのベクトルで指定される：

指定された原点と方向を持つ平行六面体：

スタイリング  (2)

色指示子は面の色を指定する：

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定することができる：

座標  (2)

2Dおよび3Dでは，平行六面体はScaled座標で指定することができる：

Offset座標を使う：

領域  (10)

埋込み次元は平行六面体が存在する空間の次元である：

幾何次元は形そのものの次元である：

帰属判定：

帰属条件：

測度：

重心：

点からの距離：

これを可視化する：

点からの符号付き距離：

これをプロットする：

最近点：

これを可視化する：

平行六面体は有界である：

領域についての境界ボックスを計算する：

Parallelepiped上で積分(Integrate)する：

この上で最適化する：

Parallelepiped上で方程式を解く：

アプリケーション  (3)

全次元のParallelepipedについては，測度値はベクトルから簡単に計算できる：

体積は行列 の行列式の絶対値に等しい：

より低い次元のParallelepipedについては，Gram行列式の平方根が使われる：

Gram行列式は とそのTransposeのドット積の行列式である：

任意の全次元のParallelepipedで，タイルを貼るように空間を埋めることができる：

特性と関係  (5)

Parallelogramは，Parallelepipedの完全2Dのケースである：

Rectangleは軸に沿った辺を持つ2DのParallelepipedである：

Cuboidは，軸に沿った辺を持つ3DのParallelepipedである：

任意のParallelepipedはCuboidのAffineTransformである：

Hexahedronは3DParallelepipedの一般化されたケースである：

Wolfram Research (2014), Parallelepiped, Wolfram言語関数， https://reference.wolfram.com/language/ref/Parallelepiped.html.

テキスト

Wolfram Research (2014), Parallelepiped, Wolfram言語関数， https://reference.wolfram.com/language/ref/Parallelepiped.html.

CMS

Wolfram Language. 2014. "Parallelepiped." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Parallelepiped.html.

APA

Wolfram Language. (2014). Parallelepiped. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Parallelepiped.html

BibTeX

@misc{reference.wolfram_2024_parallelepiped, author="Wolfram Research", title="{Parallelepiped}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Parallelepiped.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parallelepiped, organization={Wolfram Research}, title={Parallelepiped}, year={2014}, url={https://reference.wolfram.com/language/ref/Parallelepiped.html}, note=[Accessed: 22-November-2024 ]}