PowerDistribution
PowerDistribution[k,a]
represents a power distribution with domain parameter k and shape parameter a.
Details
- The probability density for value
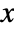in a power distribution is proportional to 
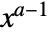for 
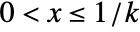and zero otherwise. - PowerDistribution allows k and a to be any positive real numbers.
- PowerDistribution allows k to be a quantity of any unit dimension, and a to be a dimensionless quantity. »
- PowerDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- PowerDistribution[k,a] represents a continuous statistical distribution supported on the interval
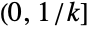and parametrized by positive real numbers k and a (called a "domain parameter" and a "shape parameter", respectively) that together determine the overall behavior of its probability density function (PDF). In general, the PDF of a power distribution is monotone increasing with its global maximum occurring at the upper boundary of its domain, though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of k and a. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a power distribution. Distributed[x,PowerDistribution[k,a]], written more concisely as xPowerDistribution[k,a], can be used to assert that a random variable x is distributed according to a power distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for power distributions may be given using PDF[PowerDistribution[k,a],x] and CDF[PowerDistribution[k,a],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a power distribution, EstimatedDistribution to estimate a power parametric distribution from given data, and FindDistributionParameters to fit data to a power distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic power distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic power distribution.
- TransformedDistribution can be used to represent a transformed power distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a power distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving power distributions.
- PowerDistribution is related to a number of other distributions. PowerDistribution is related to both KumaraswamyDistribution and PearsonDistribution in the sense that the PDF of PowerDistribution[1,α] is precisely equivalent to that of KumaraswamyDistribution[α,1] and PearsonDistribution[1,1-α,α-1,1,-1,0]. Moreover, PowerDistribution is a transformation (TransformedDistribution) of both ExponentialDistribution and ParetoDistribution as the PDF of PowerDistribution[k,α] is the same as the PDF of
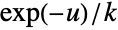and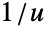 
when uExponentialDistribution[α] and when uParetoDistribution[k,α], respectively. PowerDistribution is also related to ExponentialPowerDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a power distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the shape parameter:
Kurtosis depends only on the shape parameter:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Suppose the variance of normal distribution follows PowerDistribution defined on the unit interval. Find the resulting distribution:
Properties & Relations (9)
Power distribution is closed under scaling by a positive factor:
Power distribution is closed under Max:
Relationships to other distributions:
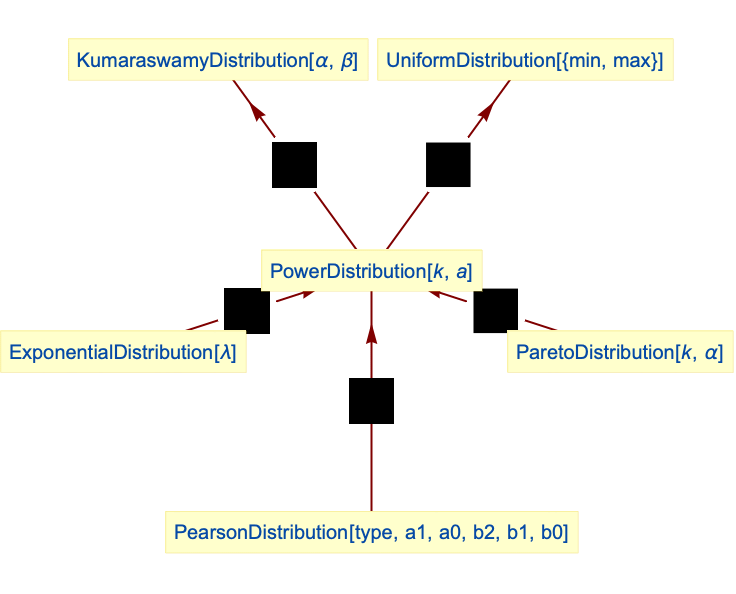
KumaraswamyDistribution simplifies to a special case of power distribution:
Power distribution is a transformation of ExponentialDistribution:
ExponentialDistribution can be obtained from power distribution:
Power distribution is a distribution of an inverse of ParetoDistribution:
UniformDistribution is a transformation of PowerDistribution:
PowerDistribution is a special case of PearsonDistribution:
Text
Wolfram Research (2010), PowerDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PowerDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "PowerDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PowerDistribution.html.
APA
Wolfram Language. (2010). PowerDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerDistribution.html