QuadraticOptimization[f,cons,vars]
求可最小化受线性约束条件 cons 限制的二次目标函数 f 的变量 vars 的值.
QuadraticOptimization[{q,c},{a,b}]
求可最小化受线性不等式约束条件 ![]() 约束的二次目标函数
约束的二次目标函数 ![]() 的向量
的向量 ![]() .
.
QuadraticOptimization[{q,c},{a,b},{aeq,beq}]
包括线性不等式约束条件 ![]() .
.
QuadraticOptimization[{q,c},…,{dom1,dom2,…}]
QuadraticOptimization[…,"prop"]
指定应返回解的属性 "prop".




QuadraticOptimization
QuadraticOptimization[f,cons,vars]
求可最小化受线性约束条件 cons 限制的二次目标函数 f 的变量 vars 的值.
QuadraticOptimization[{q,c},{a,b}]
求可最小化受线性不等式约束条件 ![]() 约束的二次目标函数
约束的二次目标函数 ![]() 的向量
的向量 ![]() .
.
QuadraticOptimization[{q,c},{a,b},{aeq,beq}]
包括线性不等式约束条件 ![]() .
.
QuadraticOptimization[{q,c},…,{dom1,dom2,…}]
QuadraticOptimization[…,"prop"]
指定应返回解的属性 "prop".
更多信息和选项








- 二次优化也称为二次规划 (QP)、混合整数二次规划 (MIQP) 或线性约束二次优化.
- 二次优化通常用于诸如参数拟合、投资组合优化和几何距离之类的问题.
- 二次优化是凸优化问题,可用实数、整数或复数变量高效地进行全局求解.
- 二次优化求的是能解原始问题的
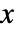 : »
: » -
最小化 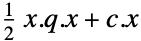
受限于约束条件 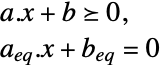
其中 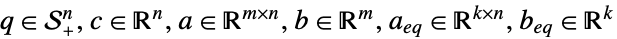
- 空间
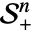 由对称半正定矩阵组成.
由对称半正定矩阵组成. - 混合整数二次优化求能解以下问题的
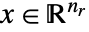 和
和 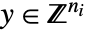 :
: -
最小化 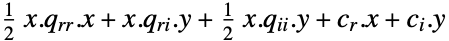
受限于约束条件 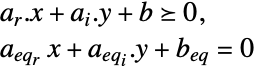
其中 ![(q_(rr) q_(ri); TemplateBox[{{q, _, {(, {r, , i}, )}}}, Transpose] q_(ii)) in S_+^n,c_r in R^(n_r),c_i in R^(n_i),a_r in R^(mxn_r),a_i in R^(mxn_i),b in R^m,a_(eq_r) in R^(kxn_r),a_(eq_i) in R^(kxn_i)b_(eq) in R^k (q_(rr) q_(ri); TemplateBox[{{q, _, {(, {r, , i}, )}}}, Transpose] q_(ii)) in S_+^n,c_r in R^(n_r),c_i in R^(n_i),a_r in R^(mxn_r),a_i in R^(mxn_i),b in R^m,a_(eq_r) in R^(kxn_r),a_(eq_i) in R^(kxn_i)b_(eq) in R^k](Files/QuadraticOptimization.zh/15.png)
- 当目标函数取实数值时,QuadraticOptimization 在内部将
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/QuadraticOptimization.zh/16.png) 转换为实变量
转换为实变量 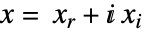 (其中
(其中 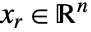 ,
,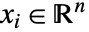 )进行求解.
)进行求解. - 变量指定 vars 应该是一个列表,其中的元素按以下形式给出变量:
-
v 名称为 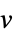 的变量,维度由推断而得
的变量,维度由推断而得v∈Reals 实标量变量 v∈Integers 整数标量变量 v∈Complexes 复标量变量 v∈ℛ 限制在几何区域 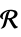 内的向量变量
内的向量变量v∈Vectors[n,dom] 位于 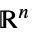 或
或 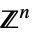 的向量变量
的向量变量v∈Matrices[{m,n},dom] 位于 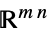 或
或 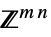 的矩阵变量
的矩阵变量 - 可用以下形式指定约束条件 cons:
-
LessEqual 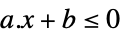
标量不等式 GreaterEqual 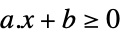
标量不等式 VectorLessEqual 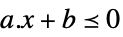
向量不等式 VectorGreaterEqual 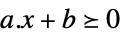
向量不等式 Equal 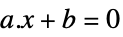
向量或标量等式 Element 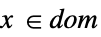
凸域或区域元素 - 对于 QuadraticOptimization[f,cons,vars],可在约束条件中包括形式为 parval 的参数方程,以定义在 f 或 cons 中使用的参数,其中 par 不在 vars 中,val 是数值或数值数组.
- 可用以下方式指定目标函数:
-
q 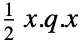
{q,c} 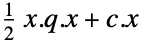
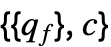
![1/2(q_f.x).(q_f.x)+c.x=1/2(x.TemplateBox[{{q, _, f}}, Transpose]).(q_f.x)+c.x 1/2(q_f.x).(q_f.x)+c.x=1/2(x.TemplateBox[{{q, _, f}}, Transpose]).(q_f.x)+c.x](Files/QuadraticOptimization.zh/36.png)
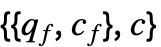
![1/2(c_f+q_f.x).(c_f+q_f.x)+c.x=1/2(x.TemplateBox[{{q, _, f}}, Transpose]+c_f).(q_f.x+c_f)+c.x 1/2(c_f+q_f.x).(c_f+q_f.x)+c.x=1/2(x.TemplateBox[{{q, _, f}}, Transpose]+c_f).(q_f.x+c_f)+c.x](Files/QuadraticOptimization.zh/38.png)
- 在因式形式中,
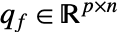 ,
, .
. - 原始最小化问题有相关的最大化问题,即拉格朗日对偶问题. 对偶最大值始终小于或等于原始最小值,因此它给出了下限. 对偶最大值点提供了有关原问题的信息,包括最小值对约束条件变化的敏感性.
- 下面给出了目标函数为
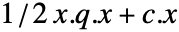 的二次优化的拉格朗日对偶问题: »
的二次优化的拉格朗日对偶问题: » -
最大化 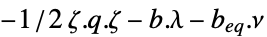
受限于约束条件 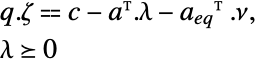
其中 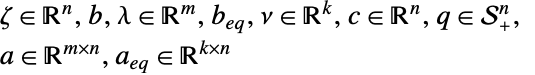
- 对于因式形式的二次目标函数
![1/2(x.TemplateBox[{{q, _, f}}, Transpose]+c_f).(q_f.x+c_f)+c.x 1/2(x.TemplateBox[{{q, _, f}}, Transpose]+c_f).(q_f.x+c_f)+c.x](Files/QuadraticOptimization.zh/45.png) ,对偶问题也可以表示为:
,对偶问题也可以表示为: -
最大化 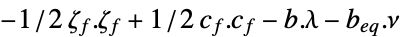
受限于约束条件 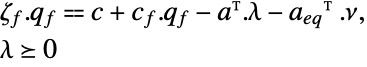
其中 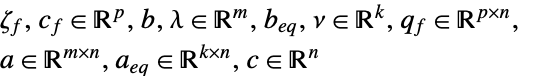
- 因式形式的对偶向量
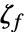 和非因式形式的对偶向量
和非因式形式的对偶向量 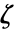 之间的关系为
之间的关系为 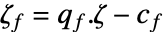 .
. - 对于二次优化,如果
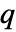 为半正定矩阵,则强对偶性成立. 这意味着如果原始最小化问题的解存在,则对偶最大化问题的解也存在,并且对偶最大值等于原始最小值.
为半正定矩阵,则强对偶性成立. 这意味着如果原始最小化问题的解存在,则对偶最大化问题的解也存在,并且对偶最大值等于原始最小值. - 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 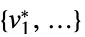
一个最小化目标函数的变量值列表 "PrimalMinimizerRules" 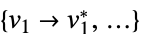
最小化 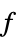 的变量值 vars={v1,…}
的变量值 vars={v1,…} "PrimalMinimizerVector" 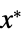
最小化 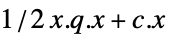 的向量
的向量"PrimalMinimumValue" 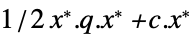
最小值 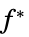
"DualMaximizer" 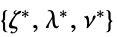
最大化 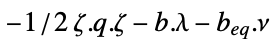
"DualMaximumValue" 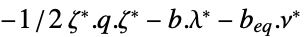
对偶最大值 "DualityGap" 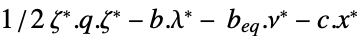
对偶值和原始最优值之间的差(由于强对偶性,差应为 0) "Slack" 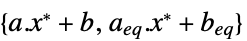
约束松弛向量 "ConstraintSensitivity" 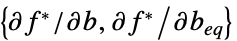
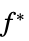 对约束条件扰动的敏感性
对约束条件扰动的敏感性"ObjectiveMatrix" 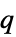
二次目标矩阵 "ObjectiveVector" 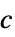
线性目标向量 "FactoredObjectiveMatrix" 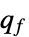
因式形式的目标函数内的矩阵 "FactoredObjectiveVector" 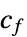
因式形式的目标函数内的向量 "LinearInequalityConstraints" 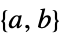
线性不等式约束矩阵和向量 "LinearEqualityConstraints" 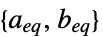
线性等式约束矩阵和向量 {"prop1","prop2",…} 解的几个属性 - 对偶最大值点的分量
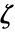 是
是 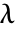 和
和 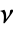 的函数,由
的函数,由 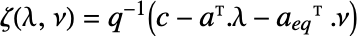 给出.
给出. - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较采用的容差 WorkingPrecision MachinePrecision 内部计算使用的精度 - 选项 Method->method 可用来指定使用的方法. 可用的方法包括:
-
Automatic 自动选择方法 "COIN" COIN 二次规划求解器 "SCS" SCS 劈分圆锥求解器 "OSQP" OSQP 二次问题的算子分裂求解器 "CSDP" CSDP 半正定优化求解器 "DSDP" DSDP 半正定优化求解器 "PolyhedralApproximation" 用多面体近似目标上境图 (objective epigraph) "MOSEK" 商用 MOSEK 凸优化求解器 "Gurobi" 商用 Gurobi 线性和二次优化求解器 "Xpress" 商用 Xpress 线性和二次优化求解器

范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (26)
基本用法 (8)
用解的属性 "PrimalMinimumValue" 获取最小化值:
用 VectorGreaterEqual (\[VectorGreaterEqual]) 和 VectorLessEqual (\[VectorLessEqual]) 指定约束条件 ![]() :
:
最小化受约束条件 ![]() 限制的
限制的 ![]() . 用 NonNegativeReals 指定约束条件
. 用 NonNegativeReals 指定约束条件 ![]() :
:
整数变量 (4)
用 Integers 指定整数域约束条件:
用 Vectors[n,Integers] 指定向量变量的整数域约束条件:
用 NonNegativeIntegers (![]() ) 指定非负整数域约束条件:
) 指定非负整数域约束条件:
用 NonPositiveIntegers (![]() ) 指定非正整数域约束条件:
) 指定非正整数域约束条件:
复变量 (3)
原始模型属性 (4)
对偶模型属性 (3)
选项 (12)
Method (5)
"PolyhedralApproximation" 用线性约束条件近似目标:
对于最小二乘型二次优化问题,"CSDP" 和 "DSDP" 比 "COIN" 或 "SCS" 慢:
对于最小二乘类二次优化问题,"CSDP","DSDP" 和 "PolyhedralApproximation" 比 "COIN" 或or "SCS" 方法慢:
用 "PolyhedralApproximation" 方法求解问题:
最小化凹函数只能使用 Method"COIN":
Tolerance (2)
WorkingPrecision (4)
MachinePrecision 是 QuadraticOptimization 中 WorkingPrecision 选项的默认设置:
如果设置 WorkingPrecisionAutomatic,QuadraticOptimization 从输入推断要使用的精度:
QuadraticOptimization 可用任意精度的数字计算结果:
如果无法算出高精度结果,发出一条消息,同时返回 MachinePrecision 的结果:
应用 (29)
基本模型转换 (7)
最大化受约束条件 ![]() 限制的
限制的 ![]() . 对目标函数取负求解最大化问题:
. 对目标函数取负求解最大化问题:
由于 QuadraticOptimization 最小化 ![]() ,矩阵乘以 2:
,矩阵乘以 2:
QuadraticOptimization 可直接进行此转换. 用 Inactive 构建目标函数以避免被运行:
最小化受约束条件 ![]() 限制的
限制的 ![]() . 将目标函数转换为
. 将目标函数转换为 ![]() ,对问题进行求解:
,对问题进行求解:
最小化受约束条件 ![]() 限制的
限制的 ![]() . 约束条件
. 约束条件 ![]() 可被解释为
可被解释为 ![]() . 根据每个约束条件对问题进行求解:
. 根据每个约束条件对问题进行求解:
最小化受约束条件 ![]() 限制的
限制的 ![]() ,其中
,其中 ![]() 是一个非递减函数,因而可代之以最小化
是一个非递减函数,因而可代之以最小化 ![]() . 对于两个问题,原始最小值点
. 对于两个问题,原始最小值点 ![]() 将保持不变. 考虑最小化受约束条件
将保持不变. 考虑最小化受约束条件 ![]() 限制的
限制的 ![]() :
:
数据拟合问题 (7)
用 DesignMatrix 构建因式形式的二次矩阵:
用 DesignMatrix 构建因式形式的二次矩阵:
拟合二次曲线离散数据,使数据的第一个和最后一个点位于曲线上:
用 DesignMatrix 构建因式形式的二次矩阵:
也可以用 Fit 通过 ![]() 正则化更高效地完成子集选择. 首先,找到最多使用
正则化更高效地完成子集选择. 首先,找到最多使用 ![]() 个基函数的正则化参数的范围:
个基函数的正则化参数的范围:
分类问题 (2)
对于此分隔问题,第 1 组必须满足 ![]() ,第 2 组必须满足
,第 2 组必须满足 ![]() . 通过最小化
. 通过最小化 ![]() 找出超平面:
找出超平面:
用 DesignMatrix 构建两组点的二次多项式数据矩阵:
几何问题 (3)
求通过最小化 ![]() 求距
求距 ![]() 最近的点. 构建目标函数时使用 Inactive Plus:
最近的点. 构建目标函数时使用 Inactive Plus:
原始最小化问题是最小化受 ![]() 限制的
限制的 ![]() . 该问题的对偶问题是最大化受
. 该问题的对偶问题是最大化受 ![]() 限制的
限制的 ![]() :
:
最小包含球的半径是最大值的 Sqrt:
使用 BoundingRegion 可有效地找到最小包含球:
投资问题 (3)
求要购买的四只股票的数量,以便获得至少 $1000 的股息并最小化风险. 与股票相关的预期收益值和协方差矩阵 ![]() 为:
为:
四只股票的单位价格为 $1. 每只股票最多可分配 $2500:
求要购买的有卖空期权的四只股票的数量,以便获得至少 $1000 的股息并最小化风险:
卖空期权允许卖出股票. 通过最小化目标函数 ![]() 给出的风险,可以算出最佳买入/卖空股票的数量:
给出的风险,可以算出最佳买入/卖空股票的数量:
第二只股票可以卖空. 因卖空而获得至少 $1000 的总投资是:
求从 20 只候选股票中选取六只股票的最佳组合,最小化风险的同时最大化回报:
投资组合优化 (1)
轨迹优化问题 (2)
最小化受约束条件 ![]() 限制的
限制的 ![]() . 可使用梯形法则近似最小化函数积分. 离散化的目标函数为
. 可使用梯形法则近似最小化函数积分. 离散化的目标函数为 ![]() :
:
可用 Indexed 函数表示约束条件 ![]() :
:
将离散化结果转换为 InterpolatingFunction:
如果 ![]() 中至少有一个元素小于零,则点
中至少有一个元素小于零,则点 ![]() 在障碍物之外. 为了强制实行该约束条件,令
在障碍物之外. 为了强制实行该约束条件,令 ![]() 为决策变量,
为决策变量,![]() 为
为 ![]() 的第
的第 ![]() 个元素,使得
个元素,使得 ![]() ,则
,则 ![]() 和
和 ![]() 足够大,可满足
足够大,可满足 ![]() :
:
最优控制问题 (2)
可用 Indexed 指定 end-condition 约束条件 ![]() :
:
将离散化结果转换为 InterpolatingFunction:
可用 Indexed 指定 end-condition 约束条件 ![]() :
:
将离散化结果转换为 InterpolatingFunction:
序列二次优化 (2)
属性和关系 (9)
QuadraticOptimization 给出目标函数的全局最小值:
Minimize 给出二次优化问题的全局精确结果:
NMinimize 可用全局方法获得近似结果:
FindMinimum 可用局部方法获得近似结果:
LinearOptimization 是 QuadraticOptimization 的特例:
SecondOrderConeOptimization 是 QuadraticOptimization 的推广:
SemidefiniteOptimization 是 QuadraticOptimization 的推广:
可能存在的问题 (6)
相关指南
-
▪
- 凸优化 ▪
- 基于矩阵的最小化 ▪
- 最优化 ▪
- 符号向量、矩阵和数组
文本
Wolfram Research (2019),QuadraticOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/QuadraticOptimization.html (更新于 2020 年).
CMS
Wolfram 语言. 2019. "QuadraticOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/QuadraticOptimization.html.
APA
Wolfram 语言. (2019). QuadraticOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/QuadraticOptimization.html 年
BibTeX
@misc{reference.wolfram_2025_quadraticoptimization, author="Wolfram Research", title="{QuadraticOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/QuadraticOptimization.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_quadraticoptimization, organization={Wolfram Research}, title={QuadraticOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/QuadraticOptimization.html}, note=[Accessed: 16-February-2026]}