QuartileSkewness

QuartileSkewness[data]

list の要素の四分位歪度係数を与える．

QuartileSkewness[data,{{a,b},{c,d}}]

パラメータ a, b, c, d で指定された四分位定義を使う．

QuartileSkewness[dist]

分布 dist の四分位歪度係数を与える．

詳細

  • QuartileSkewness[data]は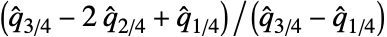によって与えられる．ただし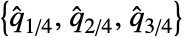，はQuartiles[data]によって与えられる．
  • 正の四分位歪度の値は，中央値 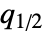が上位四分位点 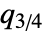よりも下位四分位点 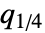に近いことを意味する．
  • 負の四分位歪度の値は，中央値 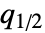が上位四分位点 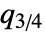に近いことを意味する．
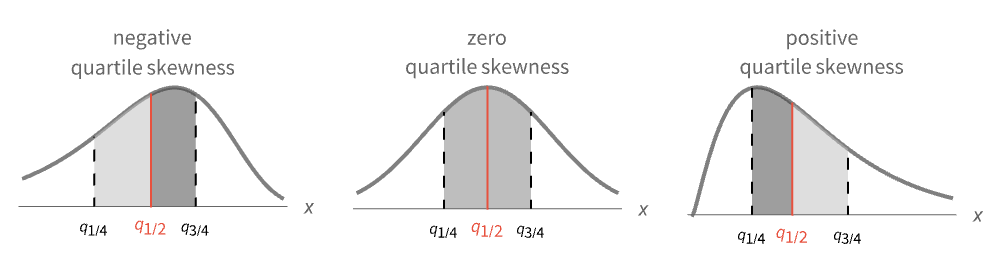
  • QuartileSkewness[data,{{a,b},{c,d}}]は，Quartiles[data, {{a,b},{c,d}}]として計算された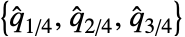を使う． »
  • 　次は，よく使われるパラメータ{{a,b},{c,d}}の選択肢である．
  • {{0, 0}, {1, 0}}経験的逆累積分布関数
    {{0, 0}, {0, 1}}線形補間（カリフォルニア法）
    {{1/2, 0}, {0, 0}}p n に最も近い番号の要素
    {{1/2, 0}, {0, 1}}線形補間（水文学者法，デフォルト）
    {{0, 1}, {0, 1}}平均を基づく推定（ワイブル法）
    {{1, -1}, {0, 1}}最頻値に基づく推定
    {{1/3, 1/3}, {0, 1}}中央値に基づく推定
    {{3/8, 1/4}, {0, 1}}正規分布推定
  • パラメータのデフォルト値は{{1/2,0},{0,1}}である． »
  • data は，以下の追加的な形式と解釈を持つことがある．
  • Association値（キーは無視される） »
    SparseArray配列として，Normal[data]に等しい »
    QuantityArray配列としての数量 »
    WeightedDataもとになっているEmpiricalDistributionに基づく »
    EventData基になっているSurvivalDistributionに基づく »
    TimeSeries, TemporalData, …ベクトルまたは配列の値（タイムスタンプは無視される） »
    Image,Image3DRGBチャンネル値またはグレースケールの強度値 »
    Audioすべてのチャンネルの振幅値 »
    DateObject, TimeObject日付のリストまたは時間のリスト »

例題

すべて開くすべて閉じる

例  (3)

厳密数のリストの四分位歪度：

日付のリストの四分位歪度：

パラメトリック分布の四分位歪度：

スコープ  (23)

基本的な用法  (8)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

他のパラメータ化を使って結果を計算する：

WeightedDataについての四分位歪度を求める：

EventDataについての四分位歪度を求める：

TemporalDataについての四分位歪度を求める：

TimeSeriesについての四分位歪度を求める：

四分位歪度は値のみに依存する：

数量を含むデータの四分位歪度を求める：

配列データ  (5)

行列のQuartileSkewnessは列ごとの範囲を与える：

テンソルのQuartileSkewnessは最初のレベルの列ごとの中央値を与える：

大きい配列に使うことができる：

入力がAssociationのとき，QuartileSkewnessはその値に作用する：

SparseArrayデータは密な配列と同じように使うことができる：

QuantityArrayの四分位歪度を求める：

画像データと音声データ  (2)

RGB画像のチャンネルごとの四分位歪度値：

グレースケール画像の四分位歪度強度値：

チャンネルの全振幅値の四分位歪度振幅：

日付と時間  (5)

日付の四分位歪度を計算する：

日付の重み付き四分位歪度を計算する：

簡単な四分位歪度と比較する：

異なる暦で与えられた日付の四分位歪度を計算する：

時間の四分位歪度を計算する：

異なる時刻帯指定の時刻の四分位歪度を計算する：

分布と過程  (3)

パラメトリック分布についての四分位歪度を求める：

派生分布についての四分位歪度：

データ分布について：

ランダム過程の時間スライスについての四分位歪度：

アプリケーション  (6)

ゼロのQuartileSkewnessは，中央値が他の四分位点から等しく離れていることを示す：

正のQuartileSkewnessは，中央値が下位四分位点に近いことを示す：

負のQuartileSkewnessは，中央値が上位四分位点に近いことを示す：

極値がある場合の非対称性についての頑健な推定を行う：

Meanに基づいた測定値は極値に大きく影響される：

ある人の5ヶ月間の毎日の歩数を含む時系列：

歩数の中央数：

歩数の分布が上位四分位点あるいは下位四分位点に向かって歪んでいるかどうかを分析する：

日ごとの歩数の頻度のヒストグラムは，中央値が上位四分位点に近いことを示している：

学級の生徒の身長の四分位歪度係数を求める：

負の四分位歪度係数は，中央値が下位四分位点により近いことを示す：

特性と関係  (3)

QuartileSkewnessは，線形に補間されたQuantileの値の関数である：

QuartileSkewnessは四分位数の関数である：

QuartileSkewnessは，中央値，第1四分位数，分散量度の関数である：

考えられる問題  (1)

QuartileSkewnessは数値を必要とする：

おもしろい例題  (1)

50個，100個，300個のサンプルについて推定されるQuartileSkewnessの分布：

Wolfram Research (2007), QuartileSkewness, Wolfram言語関数， https://reference.wolfram.com/language/ref/QuartileSkewness.html （2024年に更新）.

テキスト

Wolfram Research (2007), QuartileSkewness, Wolfram言語関数， https://reference.wolfram.com/language/ref/QuartileSkewness.html （2024年に更新）.

CMS

Wolfram Language. 2007. "QuartileSkewness." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/QuartileSkewness.html.

APA

Wolfram Language. (2007). QuartileSkewness. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QuartileSkewness.html

BibTeX

@misc{reference.wolfram_2024_quartileskewness, author="Wolfram Research", title="{QuartileSkewness}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/QuartileSkewness.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_quartileskewness, organization={Wolfram Research}, title={QuartileSkewness}, year={2024}, url={https://reference.wolfram.com/language/ref/QuartileSkewness.html}, note=[Accessed: 22-November-2024 ]}