RandomPointConfiguration

RandomPointConfiguration[pproc,reg]

観測領域 reg にある空間点過程 pproc から擬似ランダムな空間点配置を生成する．

RandomPointConfiguration[pproc,reg, n]

n 個の空間点配置の集合を生成する．

詳細とオプション

  • RandomPointConfigurationは点過程 pproc を取って点配置をSpatialPointDataオブジェクトとして生成する．
  •     
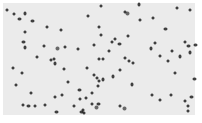
  • RandomPointConfigurationは，Wolfram言語の実行のたびに，擬似ランダムな点配置の異なる実現を与える．SeedRandomを使って特定のシードから始めることができる．
  • 同じ過程から異なる実現の集合が生成できる．
  •     
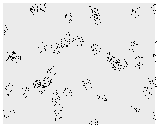
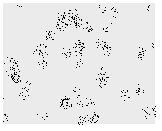
  • 観測領域 reg はSpatialObservationRegionQと同様にパラメータフリーの領域でなければならない．
  • 次は，使用可能なオプションである．
  • Method Automatic使用するメソッド
    WorkingPrecision MachinePrecision内部計算精度
  • WorkingPrecisionp の設定では，精度 p の乱数が生成される．
  • Methodの特別な設定は個々の点過程の関数ページに記載されている．
  • 次は，よく使われるMethodの設定である．
  • "MCMC"マルコフ(Markov)鎖モンテカルロ法における出生死滅過程
    "Thinning"ランダムな間引き
    "Exact"過去からのカップリング法

例題

すべて開くすべて閉じる

例  (2)

ポアソン(Poisson)点過程からのサンプル：

二項点過程からの5つの実現をサンプルとして取る：

スコープ  (5)

RandomPointConfigurationはSpatialPointDataオブジェクトを返す：

点の位置のリストを入手する：

矩形内のStrauss点過程のシミュレーションを行う：

{2,3}を中心とする単位円板内にある点を取り出す：

平面上の点を可視化する：

点過程のパラメータをシミュレーションの結果の点配置を使って推定する：

コーシー(Cauchy)点過程からのシミュレーション：

サンプルとして取った点配置からRipleyの 関数を推定し，理論的 関数と比較する：

5つの実現の組合せのシミュレーションを同じ領域上で行う：

各実現内の点の数：

別々の実現における点の分布を可視化する：

オプション  (3)

Method  (2)

さまざまなメソッドを使ってInhomogeneousPoissonPointProcessからサンプルを取る：

"Thinning"法を使う：

マルコフ鎖モンテカルロ法"MCMC"を使う：

サンプルを領域上に可視化する：

反復回数3万回でマルコフ鎖モンテカルロ法"MCMC"を使ってGibbs点過程からサンプルを取る：

WorkingPrecision  (1)

サンプル点配置をデフォルトの機械精度で生成する：

WorkingPrecisionを使ってより高精度でサンプル点配置を生成する：

アプリケーション  (2)

サンプルからPoissonPointProcessの密度を推定する：

強度推定：

非同次ポアソン点過程について，期待される点の数と点の平均数を比較する：

Wolfram Research (2020), RandomPointConfiguration, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPointConfiguration.html.

テキスト

Wolfram Research (2020), RandomPointConfiguration, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPointConfiguration.html.

CMS

Wolfram Language. 2020. "RandomPointConfiguration." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPointConfiguration.html.

APA

Wolfram Language. (2020). RandomPointConfiguration. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPointConfiguration.html

BibTeX

@misc{reference.wolfram_2024_randompointconfiguration, author="Wolfram Research", title="{RandomPointConfiguration}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPointConfiguration.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_randompointconfiguration, organization={Wolfram Research}, title={RandomPointConfiguration}, year={2020}, url={https://reference.wolfram.com/language/ref/RandomPointConfiguration.html}, note=[Accessed: 18-November-2024 ]}