WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

RecurrenceTable[eqns,expr,{n,nmax}]

再帰方程式 eqns を解くことに基づいて連続する n について expr の値のリストを生成する．

RecurrenceTable[eqns,expr,nspec]

nspec で指定された n の値の範囲で expr の値のリストを生成する．

RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]

連続するn1, n2, …について expr の値の配列を生成する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
常差分方程式  
偏差分方程式  
差分代数方程式  
系のモデル  
一般化と拡張  
オプション  
DependentVariables  
Method  
WorkingPrecision  
アプリケーション  
ロジスティック方程式  
乱数生成  
ウサギのフラクタル  
ロジスティックマップの分岐ダイアグラム  
常微分方程式の数値メソッドの比較  
標準マップ  
特性と関係  
おもしろい例題  
関連項目
関連するガイド
関連リンク
履歴
引用書式

RecurrenceTable

RecurrenceTable[eqns,expr,{n,nmax}]

再帰方程式 eqns を解くことに基づいて連続する n について expr の値のリストを生成する．

RecurrenceTable[eqns,expr,nspec]

nspec で指定された n の値の範囲で expr の値のリストを生成する．

RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]

連続するn1, n2, …について expr の値の配列を生成する．

詳細とオプション

  • eqns は指定された範囲における解が与えられた初期値または境界値によって完全に決定できる再帰方程式でなければならない．
  • eqns は a[n+i] という形式のオブジェクトを含むことができる．ただし，i は任意の固定された整数である．
  • 範囲指定 nspec はTableで使われている任意の形式持つことができる．
  • 使用可能なオプション
  • DependentVariables Automaticすべての従属変数のリスト
    Method Automatic使用するメソッド
    WorkingPrecision Automatic内部計算に使用する精度
  • DependentVariables->Automaticのとき，RecurrenceTableは与えられた方程式を分析することで従属変数を決定しようとする．
  • WorkingPrecision->Automaticとすると，厳密な入力の結果は厳密に計算され，厳密ではない入力の精度は反復ごとに適応的に決定される．
  • WorkingPrecision->p とすると，すべての反復に固定精度 p が使われる．
  • RecurrenceTable[u[t]sys,resp,{t,tmin,tmax}]は，離散時間モデルを解く際に使うことができる．sys はTransferFunctionModelまたはStateSpaceModelでよく，応答関数 resp は以下のいずれかでよい． »
  • "StateResponse"入力 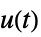に対する sys の状態応答
    "OutputResponse"入力 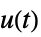に対する sys の出力応答

例題

すべて開く すべて閉じる

例  (4)

一階差分方程式の初期値問題を解く：

Wolfram Language code: RecurrenceTable[{a[n + 1] == 3a[n], a[1] == 7}, a, {n, 1, 10}]

最初のいくつかのフィボナッチ(Fibonacci)数を求める：

Wolfram Language code: RecurrenceTable[{a[n] == a[n - 1] + a[n - 2], a[1] == 1, a[2] == 1}, a, {n, 10}]
Wolfram Language code: Table[Fibonacci[n], {n, 10}]

平面の非線形写像の進化を調べる：

Wolfram Language code: RecurrenceTable[{x[n + 1] == 0.7x[n] + y[n], y[n + 1] == -0.7989995 + x[n] ^ 2, x[0] == 0.142857, y[0] == 0.33}, {x, y}, {n, 1, 2500}]//Short
Wolfram Language code: ListPlot[%, PlotRange -> All]

第一種スターリング(Stirling)数の表を計算する：

Wolfram Language code: RecurrenceTable[{s1[n, k] == s1[n - 1, k - 1] - (n - 1)s1[n - 1, k], s1[0, k] == KroneckerDelta[k]}, s1, {n, 0, 6}, {k, 0, 4}]//Grid
Wolfram Language code: Table[StirlingS1[n, k], {n, 0, 6}, {k, 0, 4}]//Grid

スコープ  (12)

常差分方程式  (6)

厳密な係数を持つ線形常差分方程式：

Wolfram Language code: RecurrenceTable[{a[n + 2] == 3n a[n + 1] + 5a[n], a[1] == 1, a[2] == 1}, a, {n, 1, 10}]

厳密ではない係数を持つ非線形常差分方程式：

Wolfram Language code: RecurrenceTable[{a[n] == 1.3a[n - 2] ^ 2 + 5.2a[n - 1], a[1] == 1, a[2] == 2}, a, {n, 1, 6}]

記号的な初期条件を持つ常差分方程式系：

Wolfram Language code: RecurrenceTable[{2 x[n + 1] + Mod[n, 5] ^ 2 y[n] == n, 5 x[n] - y[n + 1] == 7, x[1] == a, y[1] == b}, {x, y}, {n, 1, 3}]//Together

xの値のみを返す：

Wolfram Language code: RecurrenceTable[{2 x[n + 1] + Mod[n, 5] ^ 2 y[n] == n, 5 x[n] - y[n + 1] == 7, x[1] == a, y[1] == b}, x, {n, 1, 3}, DependentVariables -> {x, y}] // Together

厳密演算を使って反復する：

Wolfram Language code: RecurrenceTable[{x[n + 1] == (7/2)x[n](1 - x[n]), x[0] == (1/3)}, x, {n, 10}]

適応的演算を使い精度20から始めて反復する：

Wolfram Language code: RecurrenceTable[{x[n + 1] == (7/2)x[n](1 - x[n]), x[0] == N[(1/3), 20]}, x, {n, 10}]

反復ごとに精度が低下する：

Wolfram Language code: ListPlot[Map[Precision, %]]

固定20桁精度演算を使って反復する：

Wolfram Language code: RecurrenceTable[{x[n + 1] == (7/2)x[n](1 - x[n]), x[0] == (1/3)}, x, {n, 10}, WorkingPrecision -> 20]

機械演算を使って反復する：

Wolfram Language code: RecurrenceTable[{x[n + 1] == (7/2)x[n](1 - x[n]), x[0] == (1/3)}, x, {n, 10}, WorkingPrecision -> MachinePrecision]

ベクトルの初期条件を与えることでいくつかの値を一度に反復する：

Wolfram Language code: Grid[Partition[Map[ListPlot[#, DataRange -> {0, 1}, PlotStyle -> PointSize[0.01]]&, RecurrenceTable[{x[n + 1] == .9 Sin[π x[n]], x[0] == N[Range[0, 1000] / 1000]}, x, {n, 0, 8}]], 3]]

行列の再帰を反復する：

Wolfram Language code: Map[MatrixForm, RecurrenceTable[{m[k + 1] == m[k].(| | | | -- | -- | | .1 | 1 | | 0 | .1 |).m[k], m[0] == (| | | | - | -- | | 0 | -1 | | 1 | 0 |)}, m, {k, 3}]]

偏差分方程式  (2)

二項係数に偏再帰方程式を使う：

Wolfram Language code: RecurrenceTable[{binomial[n, k] == binomial[n - 1, k] + binomial[n - 1, k - 1], binomial[0, k] == KroneckerDelta[k]}, binomial, {n, 0, 8}, {k, 0, 8}]//Grid

非線形偏差分方程式の手続き型の解：

Wolfram Language code: RecurrenceTable[{f[n, k] == f[n - 1, k] ^ 2 + n ^ 2f[n - 1, k - 1], f[0, k] == 3k + 1.}, f, {n, 0, 20}, {k, 0, 20}];
Wolfram Language code: MatrixPlot[Log[1 + Abs[%]]]

差分代数方程式  (1)

定数係数を持つ線形差分代数方程式を解く：

Wolfram Language code: sol1 = RecurrenceTable[{y[n + 1] + z[n + 1] == y[n] - 3z[n] + 7, y[n] + 2z[n] == 1, y[0] == 1 / 2, z[0] == 1 / 4}, {y, z}, {n, 0, 4}]//Quiet

RSolveで与えられる記号解と比べる：

Wolfram Language code: RSolve[{y[n + 1] + z[n + 1] == y[n] - 3z[n] + 7, y[n] + 2z[n] == 1, y[0] == 1 / 2, z[0] == 1 / 4}, {y, z}, n]
Wolfram Language code: sol2 = Table[{y[n], z[n]} /. %[[1]], {n, 0, 4}]

系のモデル  (3)

状態空間モデルのサンプリングされた正弦波に対する状態応答と出力応答：

Wolfram Language code: sr = RecurrenceTable[Sin[t] -> StateSpaceModel[{{{0, 1}, {-0.5, 1.5}}, {{0}, {1}}, {{0, 1}}, {{0}}}, SamplingPeriod -> 1, SystemsModelLabels -> None], "StateResponse", {t, 0, 15}]
Wolfram Language code: ListStepPlot[sr, DataRange -> {0, 15}]
Wolfram Language code: or = RecurrenceTable[Sin[t] -> StateSpaceModel[{{{0, 1}, {-0.5, 1.5}}, {{0}, {1}}, {{0, 1}}, {{0}}}, SamplingPeriod -> 1, SystemsModelLabels -> None], "OutputResponse", {t, 0, 15}]
Wolfram Language code: ListStepPlot[or, DataRange -> {0, 15}]

初期条件が{1,-1}の離散時間系の状態応答：

Wolfram Language code: sr = RecurrenceTable[{Sin[t] -> StateSpaceModel[{{{0.9418, 0.2462}, {-0.2462, 0.3262}}, {{0.1958}, {-0.0291}}, {{2, 1}}, {{0}}}, SamplingPeriod -> 0.2, SystemsModelLabels -> None], {1, -1}}, "StateResponse", {t, 0, 10}]
Wolfram Language code: ListStepPlot[sr, DataRange -> {0, 10 0.2}]

2入力系の出力応答：

Wolfram Language code: or = RecurrenceTable[{Sin[k], Cos[k]} -> TransferFunctionModel[{{{z, -0.1 + z}, {1, 4}}, {{-0.5 + z, 0.5 + z}, {-0.5 + z, 0.5 + z}}}, z, SamplingPeriod -> 0.1], "OutputResponse", {k, 0, 3}]
Wolfram Language code: ListStepPlot[or, DataRange -> {0, 3 0.1}]

一般化と拡張  (3)

与えられた範囲からの値の部分集合を生成する：

Wolfram Language code: RecurrenceTable[{a[n] == a[n - 1] + a[n - 2], a[1] == 1, a[2] == 1}, a, {n, 1, 15}]
Wolfram Language code: RecurrenceTable[{a[n] == a[n - 1] + a[n - 2], a[1] == 1, a[2] == 1}, a, {n, 1, 15, 2}]

反復からの最後の値だけを得る：

Wolfram Language code: Timing[First[RecurrenceTable[{x[n + 1] == π Sin[π x[n]], x[0] == .1}, x, {n, 10 ^ 6, 10 ^ 6}]]]

次の方法はすべての値を保存する方法よりも速い：

Wolfram Language code: Timing[Last[RecurrenceTable[{x[n + 1] == π Sin[π x[n]], x[0] == .1}, x, {n, 10 ^ 6}]]]

ベクトル初期条件を使う：

Wolfram Language code: RecurrenceTable[{x[n + 1] == π Sin[π x[n]], x[0] == Range[0, 1, .1]}, x, {n, 5}]

オプション  (3)

DependentVariables  (1)

DependentVariablesを使って，いくつかの変数だけを保存したい場合にその変数を指定する：

Wolfram Language code: RecurrenceTable[{x[n + 2] == y[n], y[n + 1] == -x[n], x[0] == 1, x[1] == 0, y[0] == 0}, x, {n, 0, 3}, DependentVariables -> {x, y}]

yだけを保存する：

Wolfram Language code: RecurrenceTable[{x[n + 2] == y[n], y[n + 1] == -x[n], x[0] == 1, x[1] == 0, y[0] == 0}, y, {n, 0, 3}, DependentVariables -> {x, y}]

{y,x}の順で両方保存する：

Wolfram Language code: RecurrenceTable[{x[n + 2] == y[n], y[n + 1] == -x[n], x[0] == 1, x[1] == 0, y[0] == 0}, {y, x}, {n, 0, 3}, DependentVariables -> {x, y}]

Method  (1)

Method->{Compiled->False}を使って，Wolfram言語のコンパイラの使用を避ける：

Wolfram Language code: m = 10 ^ 6; reqn = {x[n + 1] == Nest[(4 #(1 - #))&, x[n], 2], x[0] == .314}
Wolfram Language code: Timing[Last[compiled = RecurrenceTable[reqn, x, {n, m}]]]
Wolfram Language code: Timing[Last[justrun = RecurrenceTable[reqn, x, {n, m}, Method -> {Compiled -> False}]]]

最適化による演算の変化によって，結果は異なる：

Wolfram Language code: ListPlot[Take[Abs[compiled - justrun], 50], PlotRange -> All]

WorkingPrecision  (1)

より速く反復するようにWorkingPrecision->MachinePrecisionを使う：

Wolfram Language code: reqn = {x[n + 1] == (9 / 5)If[x[n] < 1 / 2, x[n], 1 - x[n]], x[0] == 1 / 3};
Wolfram Language code: Timing[Mean[RecurrenceTable[reqn, x, {n, 10 ^ 6}, WorkingPrecision -> MachinePrecision]]]

より遅い，しかし高精度の反復のためにWorkingPrecision->p を使う：

Wolfram Language code: Timing[Mean[RecurrenceTable[reqn, x, {n, 10 ^ 6}, WorkingPrecision -> 50]]]

厳密計算には誤差が含まれないが，非常に遅くなる可能性がある：

Wolfram Language code: Timing[Mean[RecurrenceTable[reqn, x, {n, 10 ^ 4}]];]

アプリケーション  (6)

ロジスティック方程式  (1)

パラメータrの異なる値についてのロジスティック方程式の動作を調べる：

Wolfram Language code: Table[ListPlot@RecurrenceTable[{y[n + 1] == r y[n](1 - y[n]), y[0] == 1 / 3}, y, {n, 1, 600}], {r, 3.0, 3.6, 0.2}]

乱数生成  (1)

Cliffの乱数生成器を実装する：

Wolfram Language code: RecurrenceTable[{x[n + 1] == Abs[Mod[100Log[x[n]], 1]], x[0] == 0.1}, x, {n, 0, 4}]

乱数が一様分布に従うように見える：

Wolfram Language code: RecurrenceTable[{x[n + 1] == Abs[Mod[100Log[x[n]], 1]], x[0] == 0.1}, x, {n, 1, 1000}]//ListPlot

一様分布のパラメータと比較する：

Wolfram Language code: t = RecurrenceTable[{x[n + 1] == Abs[Mod[100Log[x[n]], 1]], x[0] == 0.1}, x, {n, 1, 10 ^ 5}];
Wolfram Language code: ({Mean[#1], Variance[#1], Skewness[#1], Kurtosis[#1]} & )[t]
Wolfram Language code: N[({Mean[#1], Variance[#1], Skewness[#1], Kurtosis[#1]} & )[UniformDistribution[{0, 1}]]]

ウサギのフラクタル  (1)

Douadyのウサギのフラクタルをプロットする：

Wolfram Language code: c = -0.122561 + 0.744862I;

角が-1.3-1.3 ⅈ と1.3+1.3 ⅈ の長方形の各方向に250の点を持つ初期条件：

Wolfram Language code: zinit = Table[a + I b, {a, -1.3, 1.3, 2.6 / 249}, {b, -1.3, 1.3, 2.6 / 249}];

これらの初期条件から始まりを繰り返す：

Wolfram Language code: Timing[iterates = RecurrenceTable[{z[k + 1] == z[k] ^ 2 + c, z[0] == zinit}, z, {k, 0, 20}];]

ArrayPlotを使ってフラクタルを示す：

Wolfram Language code: data = Map[If[Max[Abs[#]] ≤ 2, 1, 0]&, Flatten[iterates, {{2}, {3}, {1}}], {2}];
Wolfram Language code: ArrayPlot[data]

ロジスティックマップの分岐ダイアグラム  (1)

の1000の値について，の とからの反復を求める：

Wolfram Language code: k = 1000; r = Range[3., 4., 1 / (k - 1)]; rhs[x_ ? VectorQ] := r x(1 - x);
Wolfram Language code: iterates = RecurrenceTable[{x[n + 1] == rhs[x[n]], x[0] == ConstantArray[1. / π, k]}, x, {n, 10 ^ 4, 2 10 ^ 4}];//Timing

反復子が1から までの整数になるようにスケールし，行が に相当するように移行する：

Wolfram Language code: data = Transpose[Ceiling[iterates k]];

各値の数の対数に基づく規則を与えるように関数を定義する：

Wolfram Language code: count[data_, i_] := Module[{c, j}, {j, c} = Transpose[Tally[data]]; Transpose[{j, ConstantArray[i, Length[j]]}] -> Log[N[c]]];

各 を反復したものにCountを適用することに基づく疎行列を作る：

Wolfram Language code: S = SparseArray[Table[count[data[[i]], i], {i, k}], k]

ArrayPlotを使って分岐ダイアグラムを作成する：

Wolfram Language code: ArrayPlot[Reverse[S], ColorFunction -> "Rainbow"]

常微分方程式の数値メソッドの比較  (1)

について，オイラー(Euler)法は無条件で不安定である：

Wolfram Language code: ListPlot[Block[{h = .1}, RecurrenceTable[ {x[n + 1] == x[n] + h y[n], x[0] == 1.0, y[n + 1] == y[n] - h Sin[x[n]], y[0] == 0.}, {x, y}, {n, 0, 300}]]]

シンプレクティックオイラー法は安定しているが，大きなhについては初期条件に非常に敏感である：

Wolfram Language code: se[h_, {x0_, y0_}] := RecurrenceTable[ {x[n + 1] == x[n] + h y[n], x[0] == x0, y[n + 1] == y[n] - h Sin[x[n] + h y[n]], y[0] == y0}, {x, y}, {n, 0, 500}];ListPlot[{se[.1, {2.67, 0.}], se[1., {2.67, 0.}], se[1., {2.66, 0.}]}]

Manipulateを使って異なるベクトル場についてメソッドを比較する：

Wolfram Language code: Manipulate[ Block[{n, f1, f2, rhs, req, vfn}, vfn = vf /. {x -> x[n], y -> y[n]}; If[method === "Euler", rhs = {x[n], y[n]} + h * vfn, f1 = x[n] + h * First[vfn]; f2 = y[n] + h * (Last[vfn] /. x[n] -> f1); rhs = {f1, f2}]; req = Thread[{x[n + 1], y[n + 1]} == rhs]; ListPlot[RecurrenceTable[{req /. h -> hh, Thread[{x[0], y[0]} == p]}, {x, y}, {n, 0, Ceiling[10 ^ ls]}], PlotRange -> {{-4, 4}, {-3, 3}}, PlotLabel -> ToString[req, TraditionalForm]]], {{p, {2.67, 0}}, Locator}, {{ls, 4, "SubscriptBox[log, 10](SubscriptBox[n, max])"}, 1, 6}, {{hh, 1., "StepSize"}, 10 ^ -4, 2}, {{vf, {y, -Sin[x]}, "Vector Field"}, {{y, -x}, {y, -Sin[x]}, {y, x * (1 - x ^ 2)}}, ControlType -> PopupMenu}, {method, {"SymplecticEuler", "Euler"}}]

標準マップ  (1)

初期条件の線の標準マップによって誘発された引き延ばしと折りたたみ [詳細]：

Wolfram Language code: Block[{k = 1, m = 10000}, Grid[Partition[MapIndexed[Tooltip[ListPlot[Transpose[#1], PlotStyle -> PointSize[0.01], PlotRange -> {{0, 2π}, {-2.5, 2.5}}], n == First[#2] - 1]&, RecurrenceTable[{ x[n + 1] == Mod[y[n] + x[n] + k Sin[x[n]], 2π], x[0] == ConstantArray[N[π], m], y[n + 1] == y[n] + k Sin[x[n]], y[0] == N[2 Range[m] / (m)]}, {x, y}, {n, 0, 11}]], 3]]]

特性と関係  (3)

RSolveは次の差分方程式の記号解を求める：

Wolfram Language code: RSolve[{a[n + 1] == 2a[n] + 1, a[0] == 7}, a, n]
Wolfram Language code: Table[a[n] /. %[[1]], {n, 0, 7}]

RecurrenceTableは同じ問題の手続き型の解を生成する：

Wolfram Language code: RecurrenceTable[{a[n + 1] == 2a[n] + 1, a[0] == 7}, a, {n, 0, 7}]

RecurrenceFilterを使って信号にフィルタをかける：

Wolfram Language code: RecurrenceFilter[{{1, -(1/2)}, {1}}, {1, 0, 0, 0, 0, 0, 0, 0}]

RecurrenceTableを使って同じ結果を得る：

Wolfram Language code: RecurrenceTable[{y[n] - (1/2)y[n - 1] == DiscreteDelta[n], y[-1] == 0}, y[n], {n, 0, 7}]

RFixedPointsを使って非線形再帰方程式の固定点を求める：

Wolfram Language code: RFixedPoints[x[n + 1] == (1/2)x[n](1 - x[n]), x, n]

RStabilityConditionsを使って固定点の安定性を解析する：

Wolfram Language code: RStabilityConditions[x[n + 1] == (1/2)x[n](1 - x[n]), x, n]

RecurrenceTableを使って方程式を解く：

Wolfram Language code: sol = RecurrenceTable[{x[n + 1] == (1/2)x[n](1 - x[n]), x[0] == -9 / 10}, x, {n, 0, 20}, WorkingPrecision -> 10]

解をプロットする：

Wolfram Language code: ListPlot[sol, PlotRange -> All]

おもしろい例題  (1)

離散化されたバージョンを使って熱方程式の初期データの平坦化を可視化する：

Wolfram Language code: c = 1; k = 1 / 320; h = 0.08;
Wolfram Language code: sol = RecurrenceTable[{v[i, j] == c((1 - (2 k) / h ^ 2)v[i, j - 1] + (k(v[i + 1, j - 1] + v[i - 1, j - 1])) / h ^ 2), v[i, 0] == UnitStep[2. - i h]UnitStep[i h + 2]100}, v, {i, -70, 70}, {j, 0, 300}];
Wolfram Language code: Table[ListLinePlot[Transpose[sol][[i]], Filling -> Axis, Ticks -> None], {i, {1, 20, 100, 300}}]
Wolfram Language code: ListPlot3D[Transpose[sol], Mesh -> None, PlotStyle -> {Orange, Specularity[White, 10]}]
Wolfram Research (2008), RecurrenceTable, Wolfram言語関数， https://reference.wolfram.com/language/ref/RecurrenceTable.html （2024年に更新）.

テキスト

Wolfram Research (2008), RecurrenceTable, Wolfram言語関数， https://reference.wolfram.com/language/ref/RecurrenceTable.html （2024年に更新）.

CMS

Wolfram Language. 2008. "RecurrenceTable." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RecurrenceTable.html.

APA

Wolfram Language. (2008). RecurrenceTable. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RecurrenceTable.html

BibTeX

@misc{reference.wolfram_2026_recurrencetable, author="Wolfram Research", title="{RecurrenceTable}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RecurrenceTable.html}", note=[Accessed: 01-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_recurrencetable, organization={Wolfram Research}, title={RecurrenceTable}, year={2024}, url={https://reference.wolfram.com/language/ref/RecurrenceTable.html}, note=[Accessed: 01-November-2026]}