Reduce

Reduce[expr,vars]

通过求解关于 vars 的方程和不等式以及消除量词来约化表达式 expr.

Reduce[expr,vars,dom]

在域 dom 上的约化. dom 的选取通常是 Reals、Integers 和 Complexes.

更多信息和选项

  • expr 可以是以下表达式的任何逻辑组合：
  • lhs==rhs方程
    lhs!=rhs不等式
    lhs>rhs 或者 lhs>=rhs 不等式
    expr∈dom指定域
    {x,y,…}∈reg区域规范
    ForAll[x,cond,expr]全称量词
    Exists[x,cond,expr]存在量词
  • Reduce[expr,vars] 的结果总是描述和 expr 完全相同的数学问题.
  • Reduce[{expr1,expr2,…},vars] 等价于 Reduce[expr1&&expr2&&…,vars].
  • 默认是，Reduce[expr,vars] 假定以代数形式出现在不等式中的量为实数，而其他量为复数.
  • Reduce[expr,vars,dom] 将所有变量和参数限制在域 dom 上.
  • 如果 dom 是 Reals，或其子集如 Integers 或 Rationals ，则所有常量和函数值也限制为实数.
  • Reduce[expr&&vars∈Reals,vars,Complexes] 对假定为实数的变量进行约化，但允许函数值是复数.
  • Reduce[expr,vars,Integers] 在整数上约化 Diophantine 方程.
  • Reduce[…,x∈reg,Reals] 限制 x 位于区域 reg 内. x 的不同坐标可以使用 Indexed[x,i] 指定.
  • Reduce[expr,{x1,x2,…},…] 实际上是将 expr 写成关于 x1、x2、… 的条件组合，其中每个条件仅含有之前的 .
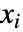  • expr 中与 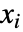无关，并且相互无关的代数变量视为独立参数.
  • 将 LogicalExpand 应用到 Reduce[expr,…] 的结果上将产生一个 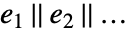形式的表达式，其中每个 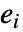可以认为是代表 expr 定义的集合中的一个独立成分.
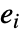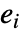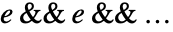  • 可以不相交且可以有不同的维数. 在应用 LogicalExpand 后，每个 有 的形式.
  • 没有 LogicalExpand 时，Reduce 默认地返回关于 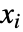的条件的一个嵌套组合，相邻级之间交替用 Or 和 And 连接.
  • 当 expr 仅包含实数域或复数域上的多项式方程和不等式时，则 Reduce 原则上总能直接对所有 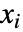求解.
  • 当 expr 涉及超越条件或整数域时，Reduce 通常将在它的结果中引入附加参数.
  • 当 expr 仅包含多项式条件时，Reduce[expr,vars,Reals] 给出 expr 的一个柱形代数分解.
  • Reduce 可以给出整数上所有线性方程和不等式解的明确表示，可以求解文献中描述的 Diophantine 方程的大部分.
  • 当 expr 仅包含实数或复数域上多项式条件是，Reduce[expr,vars] 将总要消除量词，使量词变量不出现在结果中.
  • 可以给出以下选项：
  • Backsubstitution False是否给出回代后展开的结果 »
    Cubics False是否使用明确的根式来求解所有三次方程 »
    GeneratedParameters C如果命名所产生的参数 »
    Modulus 0对整数假定的模数 »
    Quartics False是否使用明确的根式来求解所有的四次方程 »
  • Reduce[expr,{x1,x2,…},Backsubstitution->True] 产生一种格式，其中为早先 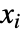产生的方程组的值被反代，因此特定 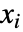条件只是极小依赖更早的 . »

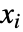范例

打开所有单元关闭所有单元

基本范例  (4)

约化方程和不等式：

用特定的域：

约化一个量化的表达式：

使用集合区域约束条件约化：

范围  (83)

基本用途  (5)

使用方程组的解集的显式描述：

使用 ToRules 和 ReplaceRepeated (//.) 列出所有解：

求不等式组的解集的显式描述：

求指定域上的解：

解集可能取决于符号参数：

表示解可能需要引入新参数；

列出前10个解：

复数域  (16)

一个线性系统：

一元多项式方程：

多元多项式方程：

多项式方程和不等式组总可以约化：

一个量化的多项式系统：

一个代数系统：

可用反函数求解得超越方程：

此例无解：

涉及椭圆函数的方程：

用特殊函数的零点求解方程：：

求解以下系统不需要黎曼假设：

闭区域上的初等函数方程：

闭区域的解析函数：

Reduce 找到一些解，但不能证明没有其它解：

复平面上一个竖直条带上的有纯虚数周期的方程：

双周期超越方程式：

可使用反函数求解的超越方程组：

有界框上的解析方程平方系统：

实数域  (26)

一个线形系统：

一元多项式方程：

一元多项式不等式：

多元多项式方程：

多元多项式不等式：

多项式方程和不等式组总可以被约化：

一个量化的多项式组：

一个代数系统：

分段方程：

分段不等式：

可用反函数求解的超越方程：

可用反函数求解的超越不等式：

涉及椭圆函数的不等式：

可用特殊函数零点求解的超越方程式：

可用特殊函数零点求解的超越不等式：

指数对数方程：

高次稀疏多项式方程：

带有高次根的代数方程：

带有无理实数冪的方程式：

指数对数不等式：

有界区间的初等函数方程：

有界区间的全纯函数方程：

有界区间内的亚纯函数不等式：

实数域上的周期性初等函数方程：

可用反函数求解的超越系统：

对第一个变量为指数-对数函数而对其它变量为多项式的系统：

量化系统：

对第一变量为初等函数且有界而对其它变量为多项式的系统：

量化系统：

在第一个变量中系统解析且有界，在其他变量中为多项式：

量化系统：

有界框上的解析方程平方系统：

整数域  (13)

线形方程组：

线形方程和不等式组：

一元多项式方程：

一元多项式不等式：

二元二次方程：

一个 Thue 方程：

一个平方和的方程：

毕达哥拉斯（Pythagoras）方程（勾股定理）：

方程和不等式的有界系统：

无解的高次系统：

超越的丢番图（Diophantine）系统：

同余的多项式组：

具有无理系数的丢番图方程：

模域  (5)

一个线形系统：

一个一元多项式方程：

一个多元多项式方程：

一个多项式方程和不等式系统：

约化一个量化的多项式系统：

有限域  (4)

一元方程：

线性方程组：

多项式方程组：

含有 quantifier 的方程组：

混合域  (4)

实数和复数变量的混合：

求出满足 为小于 的实数的 的实数值和 的复数值：

约化含有 Abs[x] 的不等式：

绘制解集：

混合整数和实变量：

几何区域  (10)

把变量限制在二维空间的基本几何区域内：

绘制解：

把变量限制于三维空间内的基本几何区域：

绘制解的图线：

把三维区域投影到 - 平面：

绘制投影图线：

一个隐式定义的区域：

一个使用参数定义的区域：

导出区域：

的解限制于交集：

在区域的笛卡尔积上消去量词：

依赖于参数的区域：

的条件：

使用 指定 是 内的一个向量：

在这种情况下， 是 内的一个向量：

选项  (6)

Backsubstitution  (1)

因为在变量列表中 y 出现在 x 之后，Reduce 可能用 x 表示 y 的解：

设置 Backsubstitution->True 后，Reduce 给出 y 的明确数值结果：

Cubics  (1)

默认情况下 Reduce 不使用以根式表达的三次方程解的通式：

设置 Cubics->True 时，Reduce 按根式求解所有三次方程：

GeneratedParameters  (1)

Reduce 可能引入新的参数来表示解：

用 GeneratedParameters 控制参数如何产生：

Modulus  (1)

在模 9 的整数上求解方程：

Quartics  (1)

默认情况下 Reduce 不使用以根式表达的四次方程解的通式：

设置 Quartics->True，Reduce 按根式求解所有四次方程：

WorkingPrecision  (1)

用精确计算来求解会花费很长时间：

当设置为 WorkingPrecision->100 时，Reduce 能快速求解，但结果可能不正确：

应用  (9)

基本应用  (1)

证明一个三角形的 、 和 边的几何不等性：

证明三角形的不等性：

证明锐角三角形的不等性：

多项式根问题  (1)

找出使得四次方程所有根都相等的条件：

使用量词消去：

使用 Subresultants:

参数化问题  (1)

绘制一个由隐含描述给出的空间曲线：

绘制该空间曲线在 - 平面上的投影：

整数问题  (3)

求出一个 Pythagorean 三元组（满足勾股定理）：

求出一个 Pythagorean 三元组的序列：

求出用 10 分、23 分和 37 分邮票付 $2.27 邮资的方式：

用 IntegerPartitions 可以完成同样的任务：

证明只有五个正多面体：

一个正 -面体的每个面贡献 条边，但是由于它们是共享的，所以它们被计算两次：

一个正 -面体的每个面贡献 个顶点，但是由于它们是共享的，所以它们被计算 次：

使用欧拉公式 ，求面的数目：

为了使最后一个公式有正确定义，分母必须是正整数：

因此有以下五种情况：

把它与 PolyhedronData 中的实际数目相比较：

几何问题  (3)

区域 ℛ 是 的一个子集，如果 为真. 证明Disk[{0,0},{2,1}] 是 Rectangle[{-2,-1},{2,1}] 的子集：

绘制图线：

证明 Cylinder[]⊆Ball[{0,0,0},2]:

绘制图线：

对于有限点集 ，点 的 Voronoi 单元可以使用 定义，它对应于与 比任何其他店 更近的所有点，其中 . 求 Voronoi 单元的简单公式，使用 Reduce:

与 pts〚1〛 相关联的Voronoiis 单元由下面给出：

所得单元由半平面的交集给出：

求所有 Voronoi 单元的简单公式：

绘制图线：

属性和关系  (10)

约化后的结果与原先的系统等价：

可用 ToRules 和 ReplaceRepeated 对有限解集实施回代：

用 Expand 简化含有简单根式的代换结果：

用 RootReduce 简化含有代数数的表达式：

用 FindInstance 找出解的个例：

Solve 以替代规则的形式表示复方程的解：

Solve 省略含有有关参数的方程的解：

对超越方程，Solve 可能不能给出全部解：

利用反函数，可使 Solve 快速地找出一些解：

求出全部解，需花很多时间，而且解可能会很大：

求 的值， 使 x==2 是一个解：

SolveAlways 给出使复方程式永远成立的参数的值：

利用 Reduce 解决相同问题：

Resolve 消除量词，有可能并不求解所得的无量词系统：

Eliminate 去除复方程组中的变量：

利用 Resolve 求解相同问题：

Reduce 还进一步求解所得方程：

可能存在的问题  (3)

因为 出现在不等式中，假定它为实数； 可以是复数：

当指定定义域 Reals 时，要求 、 和 Sqrt[x] 是实数：

这要求不等式的两边是实数的情况下， 为复数：

Reduce 不能解决依赖于 Wolfram 语言函数的分支切割的方程式：

将第一条件非零的区域制图：

输入方程的可移动奇点通常不被视为有效解：

然而，解可能包括可移动的奇点，这些奇点会被自动简化消去：

处的可移动奇点可通过求值消去：

这里， 处的可移动奇点被 Together 消去，用于预处理方程：

巧妙范例  (1)

直接利用极限的定义，求出 的垂直渐近线：

Wolfram Research (1988)，Reduce，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Reduce.html （更新于 2024 年）.

文本

Wolfram Research (1988)，Reduce，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Reduce.html （更新于 2024 年）.

CMS

Wolfram 语言. 1988. "Reduce." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Reduce.html.

APA

Wolfram 语言. (1988). Reduce. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Reduce.html 年

BibTeX

@misc{reference.wolfram_2024_reduce, author="Wolfram Research", title="{Reduce}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Reduce.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_reduce, organization={Wolfram Research}, title={Reduce}, year={2024}, url={https://reference.wolfram.com/language/ref/Reduce.html}, note=[Accessed: 22-November-2024 ]}