RegionDisjoint
✖
RegionDisjoint
詳細とオプション

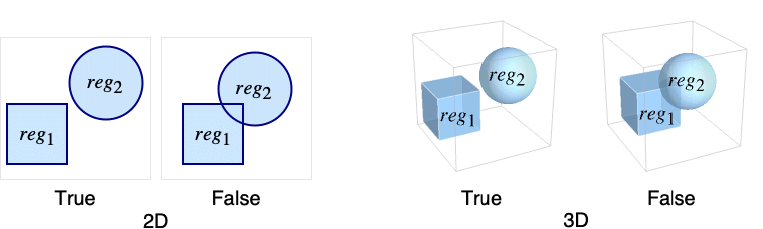
- 領域 reg1と reg2は,reg1と reg2の両方に属する点がない場合は互いに素である.
- すべての regiがパラメータを含まない領域である,つまりConstantRegionQ[regi]がTrueであれば,その領域は点集合であり,一般にTrueかFalseが返される.
- regiの中にパラメータに依存するものがある,つまりConstantRegionQ[regi]がFalseであれば,regiは領域の族を表し,RegionDisjointは領域が互いに素であるようなパラメータの条件を計算しようとする.
- 次は使用可能なオプションである.
-
Assumptions $Assumptions パラメータについて行う仮定 GenerateConditions False パラメータについての条件を生成するかどうか
例題
すべて開くすべて閉じる例 (2)基本的な使用例
https://wolfram.com/xid/0cps1hws2eafue-bwhjpw
https://wolfram.com/xid/0cps1hws2eafue-2rib4
https://wolfram.com/xid/0cps1hws2eafue-ch8cm5

https://wolfram.com/xid/0cps1hws2eafue-bjcd6
https://wolfram.com/xid/0cps1hws2eafue-bgxf3h
スコープ (17)標準的な使用例のスコープの概要
基本的な用法 (5)
https://wolfram.com/xid/0cps1hws2eafue-w6qsve
https://wolfram.com/xid/0cps1hws2eafue-02ahd7
https://wolfram.com/xid/0cps1hws2eafue-30xgaw

https://wolfram.com/xid/0cps1hws2eafue-rjig01
https://wolfram.com/xid/0cps1hws2eafue-h0qhxp
https://wolfram.com/xid/0cps1hws2eafue-q6upsg
https://wolfram.com/xid/0cps1hws2eafue-tnzyl9
https://wolfram.com/xid/0cps1hws2eafue-w8dsx6

https://wolfram.com/xid/0cps1hws2eafue-skw31u
https://wolfram.com/xid/0cps1hws2eafue-7m7agj
https://wolfram.com/xid/0cps1hws2eafue-4c84kt


https://wolfram.com/xid/0cps1hws2eafue-4yd22o
https://wolfram.com/xid/0cps1hws2eafue-2gdpbp
https://wolfram.com/xid/0cps1hws2eafue-79mtfs
基本的な領域 (4)
https://wolfram.com/xid/0cps1hws2eafue-6v3c9q
https://wolfram.com/xid/0cps1hws2eafue-uiw53u
Ball:
https://wolfram.com/xid/0cps1hws2eafue-0a693w
https://wolfram.com/xid/0cps1hws2eafue-586b1i
Pointを含む![]() 内の領域:
内の領域:
https://wolfram.com/xid/0cps1hws2eafue-i2fp1e
https://wolfram.com/xid/0cps1hws2eafue-fcyt2v
https://wolfram.com/xid/0cps1hws2eafue-rvnbj1
Line:
https://wolfram.com/xid/0cps1hws2eafue-gnymc0
https://wolfram.com/xid/0cps1hws2eafue-fw05sb
https://wolfram.com/xid/0cps1hws2eafue-vkk3wa
https://wolfram.com/xid/0cps1hws2eafue-45f5fx
https://wolfram.com/xid/0cps1hws2eafue-if4go9
https://wolfram.com/xid/0cps1hws2eafue-df44np

https://wolfram.com/xid/0cps1hws2eafue-0aeidt
https://wolfram.com/xid/0cps1hws2eafue-te9loc
https://wolfram.com/xid/0cps1hws2eafue-3el84j
Pointを含む![]() 内の領域:
内の領域:
https://wolfram.com/xid/0cps1hws2eafue-0q3l4s
https://wolfram.com/xid/0cps1hws2eafue-bc0xud
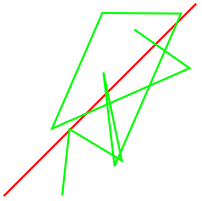
Line:
https://wolfram.com/xid/0cps1hws2eafue-43jbwg
https://wolfram.com/xid/0cps1hws2eafue-pqbwax
https://wolfram.com/xid/0cps1hws2eafue-t559ku
https://wolfram.com/xid/0cps1hws2eafue-uaqco4
https://wolfram.com/xid/0cps1hws2eafue-66pdr2
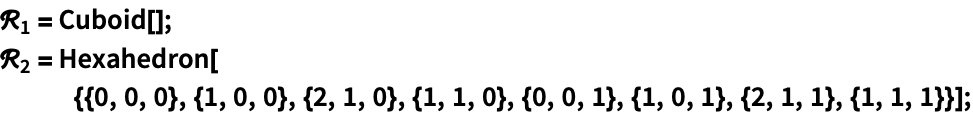
https://wolfram.com/xid/0cps1hws2eafue-35c0r8
https://wolfram.com/xid/0cps1hws2eafue-g2ry70
https://wolfram.com/xid/0cps1hws2eafue-g1mnn1
https://wolfram.com/xid/0cps1hws2eafue-3j14kp
https://wolfram.com/xid/0cps1hws2eafue-ilyuwb
https://wolfram.com/xid/0cps1hws2eafue-o1w6u8
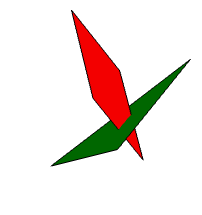
![]() 内のCuboidとParallelepipedを含む
内のCuboidとParallelepipedを含む![]() 内の領域:
内の領域:
https://wolfram.com/xid/0cps1hws2eafue-02h4ee
https://wolfram.com/xid/0cps1hws2eafue-29ru1s
https://wolfram.com/xid/0cps1hws2eafue-ufst9o
https://wolfram.com/xid/0cps1hws2eafue-8t7at1
数式定義領域 (4)
https://wolfram.com/xid/0cps1hws2eafue-yhhbit
https://wolfram.com/xid/0cps1hws2eafue-uj1qf1
https://wolfram.com/xid/0cps1hws2eafue-hukmm5
https://wolfram.com/xid/0cps1hws2eafue-jgs1z1
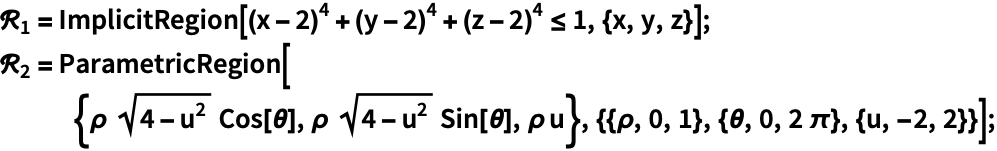
https://wolfram.com/xid/0cps1hws2eafue-eie8c4
https://wolfram.com/xid/0cps1hws2eafue-w59lx6
https://wolfram.com/xid/0cps1hws2eafue-hic6g2
メッシュ領域 (3)
![]() 内のMeshRegionを比較する:
内のMeshRegionを比較する:
https://wolfram.com/xid/0cps1hws2eafue-5yev98
https://wolfram.com/xid/0cps1hws2eafue-ciss1i
https://wolfram.com/xid/0cps1hws2eafue-6p9mf1
https://wolfram.com/xid/0cps1hws2eafue-9eeqmu

https://wolfram.com/xid/0cps1hws2eafue-pmpsgg
https://wolfram.com/xid/0cps1hws2eafue-ron1r2
https://wolfram.com/xid/0cps1hws2eafue-83vd07

https://wolfram.com/xid/0cps1hws2eafue-lz7nun
![]() 内のBoundaryMeshRegionを比較する:
内のBoundaryMeshRegionを比較する:
https://wolfram.com/xid/0cps1hws2eafue-ki5zz3
https://wolfram.com/xid/0cps1hws2eafue-bt2ml0
https://wolfram.com/xid/0cps1hws2eafue-5m2w0g
https://wolfram.com/xid/0cps1hws2eafue-mmhs4a

https://wolfram.com/xid/0cps1hws2eafue-baxiqs
https://wolfram.com/xid/0cps1hws2eafue-hyseqv
https://wolfram.com/xid/0cps1hws2eafue-zty52f

https://wolfram.com/xid/0cps1hws2eafue-ju4qkk
![]() 内のMeshRegionとBoundaryMeshRegionを比較する:
内のMeshRegionとBoundaryMeshRegionを比較する:
https://wolfram.com/xid/0cps1hws2eafue-eq7jc5
https://wolfram.com/xid/0cps1hws2eafue-n3t5rq
https://wolfram.com/xid/0cps1hws2eafue-w76nww
https://wolfram.com/xid/0cps1hws2eafue-t4fi8f
https://wolfram.com/xid/0cps1hws2eafue-xmhkjc

https://wolfram.com/xid/0cps1hws2eafue-vj7fl4
派生領域 (1)
BooleanRegionを比較する:
https://wolfram.com/xid/0cps1hws2eafue-pk317t
https://wolfram.com/xid/0cps1hws2eafue-15qu2j
オプション (2)各オプションの一般的な値と機能
Assumptions (1)
GenerateConditions (1)
アプリケーション (6)この関数で解くことのできる問題の例
ビュフォン(Buffon)の針の問題のシミュレーションを行うことで ![]() を推定する:
を推定する:
https://wolfram.com/xid/0cps1hws2eafue-2il9vg

https://wolfram.com/xid/0cps1hws2eafue-wlrn4t
https://wolfram.com/xid/0cps1hws2eafue-ue779m
https://wolfram.com/xid/0cps1hws2eafue-jod63o
https://wolfram.com/xid/0cps1hws2eafue-evtvyh

https://wolfram.com/xid/0cps1hws2eafue-vmji9a
https://wolfram.com/xid/0cps1hws2eafue-wb0wi4
https://wolfram.com/xid/0cps1hws2eafue-xqccep
https://wolfram.com/xid/0cps1hws2eafue-81bjn2
https://wolfram.com/xid/0cps1hws2eafue-ftu5x1

https://wolfram.com/xid/0cps1hws2eafue-w1gvne
https://wolfram.com/xid/0cps1hws2eafue-4p25ou
https://wolfram.com/xid/0cps1hws2eafue-s9dghf
https://wolfram.com/xid/0cps1hws2eafue-x5zsoj
https://wolfram.com/xid/0cps1hws2eafue-tg8ujy
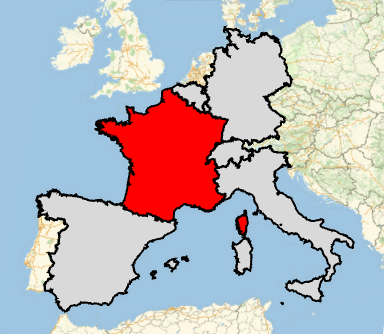
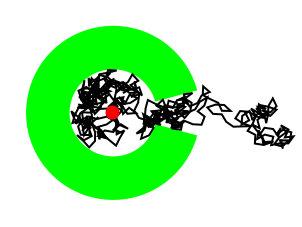
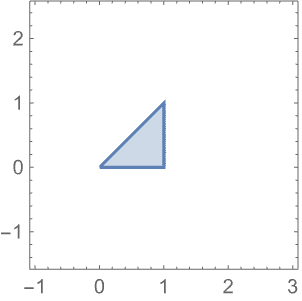
単位正方形がアニュラスと互いに素であるすべての位置を求める:
https://wolfram.com/xid/0cps1hws2eafue-59poq7
https://wolfram.com/xid/0cps1hws2eafue-4rztjs
https://wolfram.com/xid/0cps1hws2eafue-xjaxyl
https://wolfram.com/xid/0cps1hws2eafue-1eu4a3
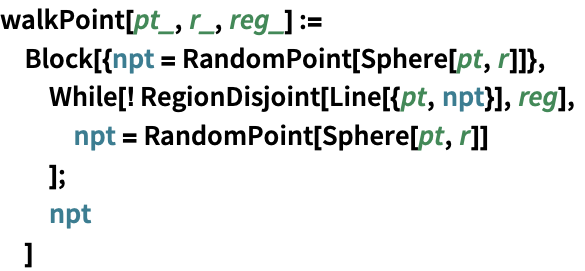
https://wolfram.com/xid/0cps1hws2eafue-2t78a9
https://wolfram.com/xid/0cps1hws2eafue-v10re3
https://wolfram.com/xid/0cps1hws2eafue-pootx3
https://wolfram.com/xid/0cps1hws2eafue-2vflrc
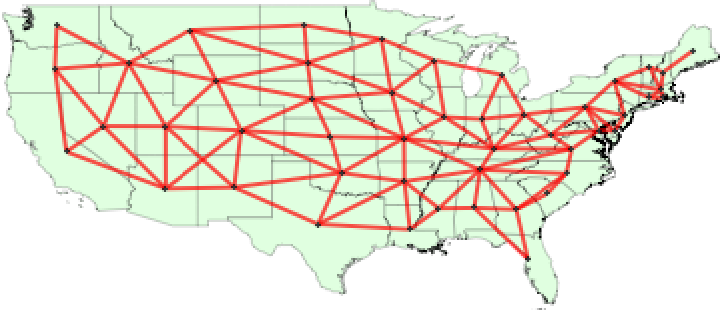
アメリカ合衆国の州境を接する各州を接続するネットワークを作る:
https://wolfram.com/xid/0cps1hws2eafue-y5c135
https://wolfram.com/xid/0cps1hws2eafue-b398l5
RegionDisjointがFalseを返すときは,2つの州の多角形が接している:
https://wolfram.com/xid/0cps1hws2eafue-gl3e7l
https://wolfram.com/xid/0cps1hws2eafue-wcikml
https://wolfram.com/xid/0cps1hws2eafue-q69f2g

https://wolfram.com/xid/0cps1hws2eafue-iinn7p
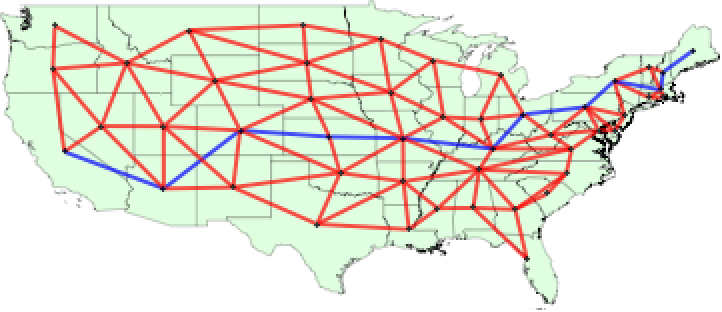
最も不連続の度合いが大きいのは,メイン州と最西部の各州である:
https://wolfram.com/xid/0cps1hws2eafue-f2e723
メイン州からカリフォルニア州までの経路を求め,ハイライトする:

https://wolfram.com/xid/0cps1hws2eafue-6ujoa4
https://wolfram.com/xid/0cps1hws2eafue-wvubzf
特性と関係 (4)この関数の特性および他の関数との関係
https://wolfram.com/xid/0cps1hws2eafue-qxxixn
https://wolfram.com/xid/0cps1hws2eafue-zxr7hs
https://wolfram.com/xid/0cps1hws2eafue-ga16k4
https://wolfram.com/xid/0cps1hws2eafue-pm8r3m
https://wolfram.com/xid/0cps1hws2eafue-szw6pm
非空の領域について,RegionEqualとRegionWithinは,RegionDisjointがTrueを返すときはFalseを返す:
https://wolfram.com/xid/0cps1hws2eafue-8azms6
https://wolfram.com/xid/0cps1hws2eafue-dp28x5
https://wolfram.com/xid/0cps1hws2eafue-28i8v5
https://wolfram.com/xid/0cps1hws2eafue-2vh1ks
FindInstanceを使って2つの領域の共通部分にある点を求める:
https://wolfram.com/xid/0cps1hws2eafue-ecv99p
https://wolfram.com/xid/0cps1hws2eafue-i0zv76
https://wolfram.com/xid/0cps1hws2eafue-vjwpmf
https://wolfram.com/xid/0cps1hws2eafue-mccqg1
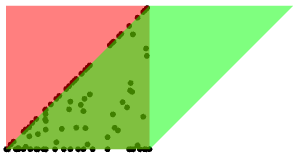
RandomPointを使って2つの領域の共通部分にある点の一様サンプリングを求める:
https://wolfram.com/xid/0cps1hws2eafue-gpkt0l
https://wolfram.com/xid/0cps1hws2eafue-o0kf7b

Reduceを使って2つの領域が重なる箇所を求める:
https://wolfram.com/xid/0cps1hws2eafue-42jril
https://wolfram.com/xid/0cps1hws2eafue-ly4r2m
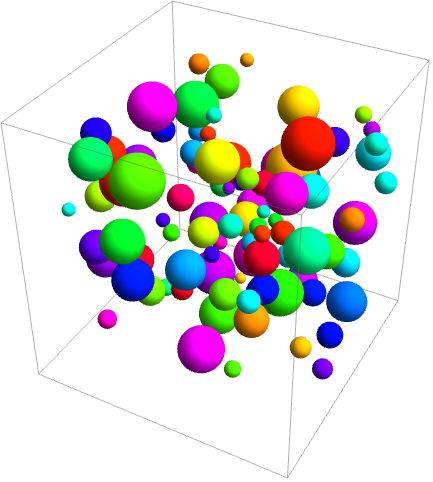
おもしろい例題 (1)驚くような使用例や興味深い使用例
https://wolfram.com/xid/0cps1hws2eafue-8pz9b5
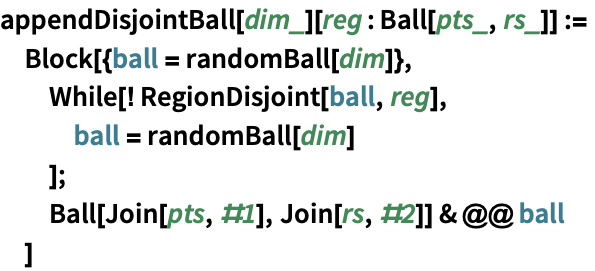
https://wolfram.com/xid/0cps1hws2eafue-r7mtxb
https://wolfram.com/xid/0cps1hws2eafue-ks2qb0
https://wolfram.com/xid/0cps1hws2eafue-fqtjp7
https://wolfram.com/xid/0cps1hws2eafue-sf4m1g

https://wolfram.com/xid/0cps1hws2eafue-4892t8
https://wolfram.com/xid/0cps1hws2eafue-69b9tg
Wolfram Research (2017), RegionDisjoint, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegionDisjoint.html.テキスト
Wolfram Research (2017), RegionDisjoint, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegionDisjoint.html.
Wolfram Research (2017), RegionDisjoint, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegionDisjoint.html.CMS
Wolfram Language. 2017. "RegionDisjoint." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDisjoint.html.
Wolfram Language. 2017. "RegionDisjoint." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDisjoint.html.APA
Wolfram Language. (2017). RegionDisjoint. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDisjoint.html
Wolfram Language. (2017). RegionDisjoint. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDisjoint.htmlBibTeX
@misc{reference.wolfram_2025_regiondisjoint, author="Wolfram Research", title="{RegionDisjoint}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionDisjoint.html}", note=[Accessed: 11-July-2025
]}BibLaTeX
@online{reference.wolfram_2025_regiondisjoint, organization={Wolfram Research}, title={RegionDisjoint}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionDisjoint.html}, note=[Accessed: 11-July-2025
]}