StableDistribution
StableDistribution[type,α,β,μ,σ]
安定指数 α,歪度母数 β,位置母数 μ,尺度母数 σ の安定分布 Stypeを表す.
詳細

- 独立同分布に従う安定確率変数の線形結合もまた安定してる.
- 安定分布は自身の特性関数
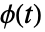 によって定義される.この特性関数は,任意の
によって定義される.この特性関数は,任意の 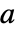 と
と 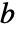 に対して
に対して 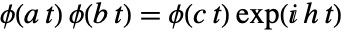 であるような
であるような 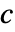 と
と 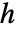 が存在する関数方程式を満足する.関数方程式の一般解には4つの母数がある.
が存在する関数方程式を満足する.関数方程式の一般解には4つの母数がある. - StableDistributionでは,0<α≤2,-1≤β≤1で,μ は任意の実数でよく,σ は任意の正の実数でよい.
- StableDistributionでは,μ と σ は単位次元が等しい任意の数量でよく,α と β は無次元量でよい. »
- CharacteristicFunction[StableDistribution[0,α,…],t]は α において連続的であり,
![exp(i mu t-sigma TemplateBox[{t}, Abs] (1+2i beta/pi sgn(t) log(TemplateBox[{{t, , sigma}}, Abs]))) alpha=1; exp(i mu t-TemplateBox[{{t, , sigma}}, Abs]^alpha (1+i beta tan((pi alpha)/2) sgn(t) (TemplateBox[{{t, , sigma}}, Abs]^(1-alpha)-1))) alpha!=1 exp(i mu t-sigma TemplateBox[{t}, Abs] (1+2i beta/pi sgn(t) log(TemplateBox[{{t, , sigma}}, Abs]))) alpha=1; exp(i mu t-TemplateBox[{{t, , sigma}}, Abs]^alpha (1+i beta tan((pi alpha)/2) sgn(t) (TemplateBox[{{t, , sigma}}, Abs]^(1-alpha)-1))) alpha!=1](Files/StableDistribution.ja/7.png) によって与えられる.
によって与えられる. - CharacteristicFunction[StableDistribution[1,α,…],t]は α において不連続的であり,
![exp(i mu t-sigma TemplateBox[{t}, Abs] (1+2 i beta/pi sgn(t) log(TemplateBox[{t}, Abs]))) alpha=1; exp(i mu t-TemplateBox[{{t, , sigma}}, Abs]^alpha (1-i beta tan((pi alpha)/2) sgn(t))) alpha!=1 exp(i mu t-sigma TemplateBox[{t}, Abs] (1+2 i beta/pi sgn(t) log(TemplateBox[{t}, Abs]))) alpha=1; exp(i mu t-TemplateBox[{{t, , sigma}}, Abs]^alpha (1-i beta tan((pi alpha)/2) sgn(t))) alpha!=1](Files/StableDistribution.ja/8.png) によって与えられる.
によって与えられる. - StableDistribution[α]はStableDistribution[1,α,0,0,1]に等しい.
- StableDistribution[α,β]はStableDistribution[1,α,β,0,1]に等しい.
- StableDistribution[α,β,μ,σ]はStableDistribution[1,α,β,μ,σ]に等しい.
- StableDistributionは,Mean,CDF,RandomVariate等の関数とともに用いることができる.
予備知識
- StableDistribution[type,α,β,μ,σ]は,2つのタイプのどちらかに属し,正の実数 σ(「尺度母数」と呼ばれる),実数 μ(「位置母数」と呼ばれる),α(
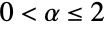 についての分布の安定性の指標),β(
についての分布の安定性の指標),β(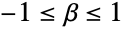 を満足する「歪度母数」)によってパラメータ化された連続統計分布を表す.これらの母数は,ともに,確率密度関数(PDF)の全体的な動作を決定する.
を満足する「歪度母数」)によってパラメータ化された連続統計分布を表す.これらの母数は,ともに,確率密度関数(PDF)の全体的な動作を決定する. - 安定分布の確率密度関数は,一般に,単峰性で単一の峰(極大値)を持つが,その全体的な形(高さ,広がり,最大値の水平位置)は分布 type のと α,β,μ,σの値両方によって決定される.さらに,確率密度関数の裾部は,type,α,β,μ,σ の値によって,「太い」(つまり,確率密度関数が大きい
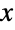 の値について非指数的に減少する)ことも「細い」(つまり,確率密度関数が大きい
の値について非指数的に減少する)ことも「細い」(つまり,確率密度関数が大きい 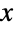 の値について指数的に減少する)こともある(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にすることができる).引数が4つ,2つ,1つのバージョンのStableDistribution[α,β,μ,σ],StableDistribution[α,β],StableDistribution[α]は,タイプ1の分布のStableDistribution[1,α,β,μ,σ],StableDistribution[1,α,β,0,1],StableDistribution[1,α,0,0,1]とそれぞれ等しい.安定分布は,母数のさまざまな値によって,安定Paretian分布,Pareto–Lévy分布(ParetoDistributionあるいはLevyDistributionと混同してはならない),Lévy α 安定分布等と呼ばれることがある.安定分布は,最小極値分布および最大極値分布(それぞれ,MinStableDistributionとMaxStableDistribution)をも異なっている.
の値について指数的に減少する)こともある(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にすることができる).引数が4つ,2つ,1つのバージョンのStableDistribution[α,β,μ,σ],StableDistribution[α,β],StableDistribution[α]は,タイプ1の分布のStableDistribution[1,α,β,μ,σ],StableDistribution[1,α,β,0,1],StableDistribution[1,α,0,0,1]とそれぞれ等しい.安定分布は,母数のさまざまな値によって,安定Paretian分布,Pareto–Lévy分布(ParetoDistributionあるいはLevyDistributionと混同してはならない),Lévy α 安定分布等と呼ばれることがある.安定分布は,最小極値分布および最大極値分布(それぞれ,MinStableDistributionとMaxStableDistribution)をも異なっている. - 安定分布はその特別なケースの多くが事実上古典的になっているが,上述した安定分布族は数学者のPaul Lévyによって1920年代の中頃にはじめて研究された.安定分布族は,線形結合の下で閉じている,つまり分布の確率密度関数が一般に閉形式を持たず,分布の特性関数 (CharacteristicFunction)によって説明されなければならないことで特徴付けられる.安定分布は,この分布がいわゆる中心極限定理の一般化に果たした役割によって,推計学や確率論で特に重要になっている.安定分布は,金融,天文学,物理学における現象のモデル化にも使われている.
- RandomVariateを使って,安定分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,StableDistribution[type,α,β,μ,σ]](より簡略な表記では xStableDistribution[type,α,β,μ,σ])を使って,確率変数 x が指定された type の安定分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 指定された type の安定分布の確率密度関数および累積分布関数は,PDF[StableDistribution[type,α,β,μ,σ],x]およびCDF[StableDistribution[type,α,β,μ,σ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が安定分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック安定分布を推定することが,FindDistributionParametersを使ってデータを安定分布にフィットすることができる.ProbabilityPlotを使って記号安定分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号安定分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された安定分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って安定分布を含む高次元分布を構築することが,ProductDistributionを使って安定分布を含む独立成分分布の結合分布を計算することができる.
- StableDistributionは,他の数多くの分布と密接な関係がある.LandauDistribution,CauchyDistribution,NormalDistribution,LevyDistributionは,LandauDistribution[μ,σ]がStableDistribution[1,1,1,μ,σ]と同じ特性関数(CharacteristicFunction) を持ち,CauchyDistribution[0,1]がStableDistribution[1,1,0,0,1]と同じ確率密度関数を持ち,NormalDistribution[μ,σ]の確率密度関数がStableDistribution[1,2,β,μ,σ/
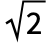 ]のそれと等しく,LevyDistribution[μ,σ]の確率密度関数がStableDistribution[1,1/2,1,μ,σ]のそれと厳密に等しいという意味で,タイプ1の安定分布の例である.定性的には,StableDistributionはPearsonDistributionに似ており,ParetoDistribution,BetaDistribution,GammaDistribution,HalfNormalDistributionとも密接な関係がある.
]のそれと等しく,LevyDistribution[μ,σ]の確率密度関数がStableDistribution[1,1/2,1,μ,σ]のそれと厳密に等しいという意味で,タイプ1の安定分布の例である.定性的には,StableDistributionはPearsonDistributionに似ており,ParetoDistribution,BetaDistribution,GammaDistribution,HalfNormalDistributionとも密接な関係がある.
例題
すべて開くすべて閉じる例 (4)
スコープ (4)
これは,StableDistributionがNormalDistributionに簡約された場合である:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (9)
株式市場の日々の対数収益率が安定分布に従うと仮定し,5年間の株価のシミュレーションを行い,それを可視化する:
株の対数収益率が安定分布に従うと仮定し,95%レベルでVaR(バリューアットリスク)を求める:
上記の分布を仮定し,現在のS&P 500指数値の95%のVaRの下げ幅を計算する:
2005年1月1日からのIBMの株価の日々の対数収益率を安定分布にフィットする:
対称安定確率変量の積と指数確率変量のベキはLinnik分布に従う:
Map–Airy分布[MathWorld]は安定した族の一つである:
サンプルの特性関数と母集団の特性関数の絶対値をプロットする:
一般化された中心極限定理は,![]() 個の独立同分布に従う確率変量
個の独立同分布に従う確率変量 ![]() (その分布関数
(その分布関数 ![]() は
は ![]() であるとき漸近線
であるとき漸近線![]() を,
を,![]() であるときに漸近線
であるときに漸近線 ![]() を持つ)のシフトされ再スケールされた総和
を持つ)のシフトされ再スケールされた総和 ![]() の分布が安定分布
の分布が安定分布 ![]() に緩やかに収束するような,
に緩やかに収束するような,![]() と
と ![]() の数列を与える:
の数列を与える:
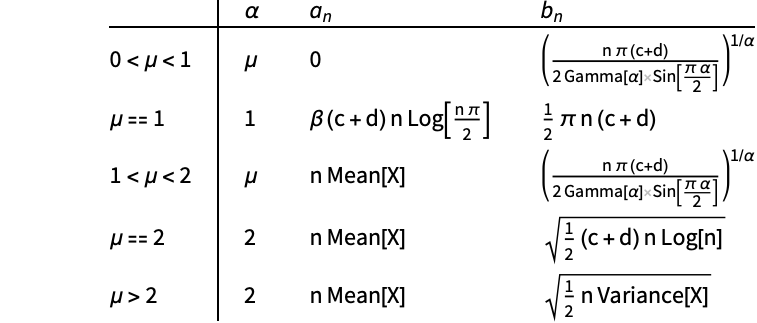
両側パレート分布を使って一般化された中心極限定理を説明する:
将来的な使用のために両側パレート分布の平均と分散を定義する:
密度プロットとデータヒストグラムを可視化する関数を定義する:
Holtsmark分布は無限ポアソン系の粒子に働く力の分布である.重力の ![]() 成分は対称安定分布に従う:
成分は対称安定分布に従う:
特性と関係 (11)
タイプ0とタイプ1の安定変数は位置母数のシフトによって互いに関連している:
安定確率変量 ![]() の
の ![]() における不連続性は,
における不連続性は,![]() の小さい変化に対するモードの検出感度に現れている:
の小さい変化に対するモードの検出感度に現れている:
タイプ0の安定分布族はシフトとスケーリングの下では閉じている:
タイプ1の安定分布族はシフトとスケーリングの下で閉じている:
![]() である安定変量は確率的に順序付けられている.すなわち,
である安定変量は確率的に順序付けられている.すなわち,![]() は
は ![]() を示唆する:
を示唆する:
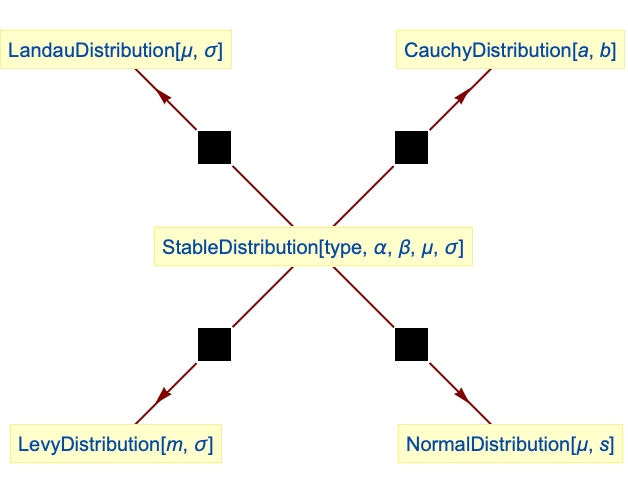
LandauDistributionは安定分布である:
CauchyDistributionは安定分布である:
NormalDistributionは安定分布である:
LevyDistributionは安定分布である:
テキスト
Wolfram Research (2010), StableDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/StableDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "StableDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/StableDistribution.html.
APA
Wolfram Language. (2010). StableDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StableDistribution.html