SurfaceIntegrate

SurfaceIntegrate[f,{x,y,…}∈surface]

surface 上の関数 f[x,y,…]のスカラー面積分を計算する．

SurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

ベクトル場{p[x,y,…],q[x,y,…],…}のベクトル面積分を計算する．

詳細とオプション

  • 面積分は流束積分としても知られている．
  • スカラー面積分は超曲面上でスカラー関数を積分する．これは，通常，曲面の面積，質量，電荷等の計算に使われる．
  • ベクトル面積分は，法線方向に曲面を通過するベクトル関数の流束の計算に使われる．典型的なベクトル関数には，液流体速度場，電場，磁場が含まれる．
  • surface 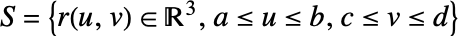上の関数 f のスカラー面積分は以下で与えられる．
  • ただし，TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm]はパラメトリック曲面要素の測定値である．
  • 超曲面 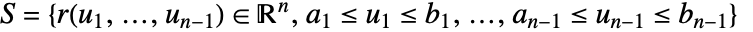上の f のスカラー面積分は以下で与えられる．

  • スカラー面積分は surface のパラメータ化および向きには依存しない．surface には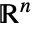における任意の 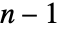次元RegionQオブジェクトを使うことができる．
  • surface 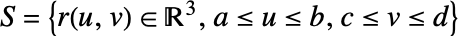上のベクトル関数 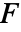のベクトル面積分は以下で与えられる．
  • ただし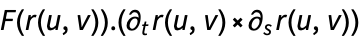，F(r(u,v)).(partial_tr(u,v)xpartial_sr(u,v))はベクトル関数 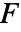の法線方向への射影であるので，法線方向の成分しか積分されない．
  • 超曲面 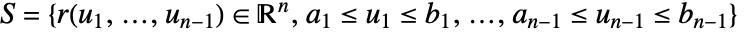上の 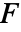のベクトル面積分は以下で与えられる．

  • ベクトル面積分はパラメータ化には依存しないが向きには依存する．
  • 超曲面の向きは曲面上の法線ベクトル場 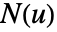で与えられる．
  • パラメトリック超曲面ParametricRegion[{r1[u1,…,un-1],…,rn[u1,…,un-1]},…]については，法線ベクトル場 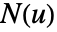はCross[∂u1r[u],…,∂un-1r[u]]であるとみなされる．
  • Wolfram言語におけるRegionQオブジェクトは向きを持たない．しかし，この関数の便宜のために，目浮きがある超曲面を得るために以下の規則を仮定することができる．
  • （次元 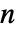の）立体および境界があるRegionQオブジェクト ℛ については，曲面が領域の境界(RegionBoundary[ℛ])で，法線は外向きであるとみなす．
  • 次は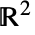，の特殊立体および想定される境界面（辺）と法線方向である．
  • Triangle外向き法線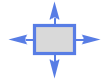
    Rectangle外向き法線
    Polygon外向き法線
    Disk外向き法線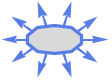
    Ellipsoid外向き法線
    Annulus外向き法線
  • 次は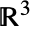，の特殊立体および想定される境界面（面）と法線方向である．
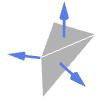
  • Tetrahedron外向き法線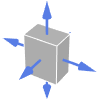
    Cuboid外向き法線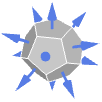
    Polyhedron外向き法線
    Ball外向き法線
    Ellipsoid外向き法線
    Cylinder外向き法線
    Cone外向き法線
  • 次は，の特殊立体および想定される面（ファセット）と法線方向である．
  • Simplex外向き法線
    Cuboid外向き法線
    Ball外向き法線
    Ellipsoid外向き法線
  • 次は，使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Automaticパラメータについての仮定を含む答を生成するかどうか
    WorkingPrecision Automatic内部計算精度
  • SurfaceIntegrateは，入力に厳密ではない数量が含まれる場合は記号メソッドと数値メソッドを組み合せて使う．

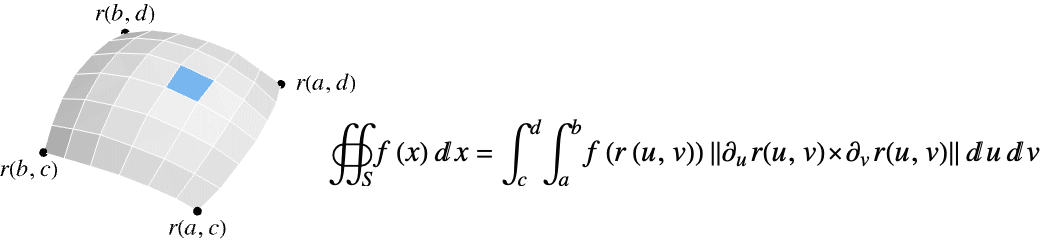
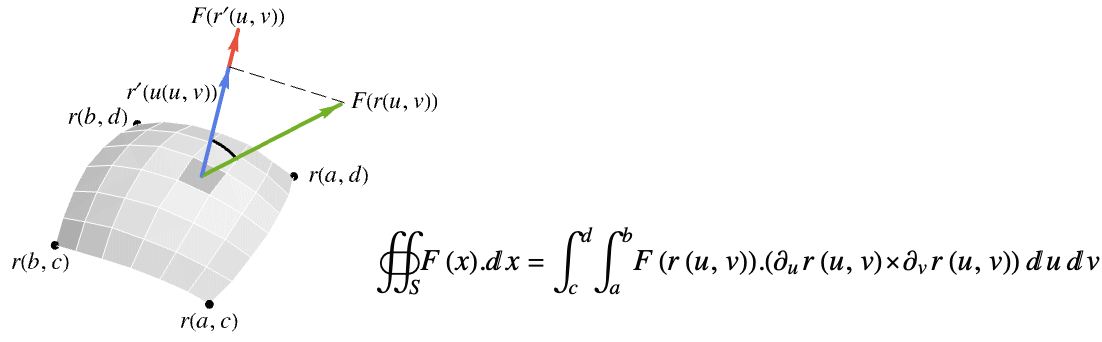
例題

すべて開くすべて閉じる

例  (6)

球面上のスカラー関数の面積分：

球面上のベクトル場の面積分：

パラメトリック曲面上のスカラー場の面積分：

パラメトリック曲面上のベクトル場の面積分：

曲面上のスカラー場の面積分：

曲面のスカラー場を可視化する：

曲面上のベクトル場の面積分：

曲面上のスカラー場を可視化する：

スコープ  (32)

基本的な用法  (5)

三次元の球曲面上のスカラー場の面積分：

三次元のベクトル場の面積分：

SurfaceIntegrateは，多くの特殊曲面に使うことができる：

パラメトリック曲面上の面積分：

SurfaceIntegrateは，3次元以外の次元に使うことができる：

スカラー関数  (5)

三次元曲面上のスカラー場の面積分：

曲面のプロット：

面積分：

スカラー場の面積分：

面積分：

球上の三次元スカラー場の面積分：

錐体の曲面上のスカラー場の面積分：

面積分：

三次元パラメトリック曲面上のスカラー場の面積分：

曲面とそのプロット：

ベクトル関数  (5)

球面上の三次元ベクトル場の面積分：

曲面上でベクトル場を可視化する：

面積分：

三角形上の三次元ベクトル場の面積分：

面積分：

三次元パラメトリック曲面上のベクトル場の面積分：

楕円体の境界上でのベクトル場の面積分：

三次元の円錐上のベクトル場の面積分：

曲面上のベクトル場の可視化：

面積分：

特殊曲面  (10)

半径 の球上のベクトル場の面積分：

原点を中心とした1辺が の立方体の境界上でのベクトル場の面積分：

四面体の境界上のベクトル場の面積分：

三角形上のベクトル場の面積分：

楕円体上のベクトル場の面積分：

円錐の境界上のベクトル場の面積分：

円柱の境界上のベクトル場の面積分：

平行六面体の境界上のベクトル場の面積分：

角柱の境界上のベクトル場の面積分：

多角形上の三次元面責分：

多角形の向きは点が与えられた順序に依存する：

パラメトリック曲面  (4)

パラメトリック曲面上のベクトル場の面積分：

パラメータ化されたドーム状の曲面上のベクトル場の面積分：

パラメータ化された円柱上の面積分：

パラメトリック双曲面上のベクトル場の面積分：

超曲面  (3)

2D内の1D超曲面上の面積分：

4D内の3D超曲面上の面積分：

面積分を使って計算された五次元曲面の体積：

オプション  (4)

Assumptions  (1)

記号パラメータには仮定が指定できる：

Assumptionsを使うと，指定された仮定のもとで有効な結果が返される：

GenerateConditions  (1)

SurfaceIntegrateは記号パラメータに使うことができる：

パラメータについての条件を生成する：

WorkingPrecision  (2)

WorkingPrecisionが指定されている場合は数値結果が与えられる：

被積分関数が有限精度なら結果の精度も有限になる：

アプリケーション  (18)

大学の微積分  (5)

原点を中心とした1辺が2の立方体の境界上の面積分：

放物体上の面積分：

円柱の側面上の面積分：

半径 の半球のシェル上の面積分：

立方体の境界上の面積分：

面積  (3)

曲面の面積：

楕円体の面積：

三角形の面積：

体積  (3)

面積分を使って計算した楕円体の体積：

面積分を使って計算した20面体の体積：

面積分を使って計算した1辺が の立方体の体積：

流れ  (3)

原点にある点電荷 によって生成された，それを囲む球上の電場の流れ：

その上を電流 が通過する，単位長あたり 個の巻線を持つ無限ソレノイドの均一な磁場の磁束に直交する円板：

線電荷密度 の無限電荷ワイヤによる電場：

電荷ワイヤ上に軸を持つ，高さ ，半径 の円柱を流れる磁束：

重心  (2)

単位密度で半径が の半球のシェルの質量：

質量の中心の 座標：

質量の中心の 座標：

質量の中心の 座標：

薄く切り取られた錐体の慣性モーメント：

軸の周囲：

軸の周囲：

軸の周囲：

従来の定理  (2)

ベクトル場 のCurl を計算する：

開曲面上の の面積分は以下のようになる：

これは，曲面の境界上における の線積分と同じである：

閉曲面上のベクトル場 の面積分を計算する：

これは，曲面内部でのDiv[f]の積分と同じである：

特性と関係  (5)

記号計算がうまくいかないときはN[SurfaceIntegrate[...]]を適用して数値解を得るとよい：

単位面積あたり単位質量の薄い三角面の質量の中心を求める：

総質量を求める：

質量の中心の 成分を求める：

質量の中心の 成分を求める：

質量の中心の 成分を求める：

質量の中心はRegionCentroidを使って求めることもできる：

単位面密度の薄い円柱型シェルの 軸の周りの慣性モーメントを求める：

答はMomentOfInertiaで計算することもできる：

四面体の面積を求める：

面積はAreaで計算することもできる：

20面体の体積を求める：

答はVolumeで計算することもできる：

おもしろい例題  (9)

面積分を使って計算した擬球の体積：

擬球の有限部分のプロット：

面積分を使った水滴型の立体の体積：

デュパン(Dupin)のサイクロイドの体積：

ボヘミアンドームの一部を横切るベクトル場の流れ：

ウォリス(Wallis)の丘の一部の上でのベクトル場の面積分：

漏斗状の曲面上のベクトル場の面積分：

Gaudi曲面の面積：

ギマール(Guimard)曲面の面積を数値的に計算する：

neiloid上のベクトル場の面積分：

Wolfram Research (2023), SurfaceIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

テキスト

Wolfram Research (2023), SurfaceIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

CMS

Wolfram Language. 2023. "SurfaceIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

APA

Wolfram Language. (2023). SurfaceIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SurfaceIntegrate.html

BibTeX

@misc{reference.wolfram_2024_surfaceintegrate, author="Wolfram Research", title="{SurfaceIntegrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_surfaceintegrate, organization={Wolfram Research}, title={SurfaceIntegrate}, year={2023}, url={https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}, note=[Accessed: 22-November-2024 ]}