WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

SystemModelCalibrate
✖
SystemModelCalibrate

[Experimental]

✖
SystemModelCalibrate[data,smodel,pars]

calibrates the parameters pars in the system model smodel according to data.

✖
SystemModelCalibrate[data,{smodel,cons},pars]

calibrates the parameters pars subject to the constraints cons.

✖

calibrates following the specification spec.

✖
SystemModelCalibrate[…,"prop"]

gives the value of the property "prop".

Details and Options

  • SystemModelCalibrate is used to calibrate parameter values in a system model to match simulation results with real-world data.
  • Given measured data 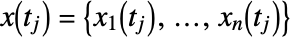from the real-world system, the goal is to calibrate parameters pars 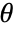in the smodel to produce simulated data 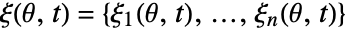that is as close as possible to the measured data.
  • The calibrated parameters are 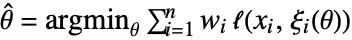, where 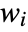are non-negative weights and ℓ is a loss function with typical form 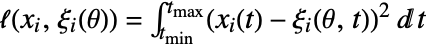, which is approximated by the sampled data as .
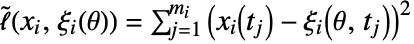  • Several quality measures of how well data and calibrated model agree can be computed as properties.
  • The system model smodel can have the following forms:
  • SystemModel[…]general system model
    StateSpaceModel[…]state-space model
    TransferFunctionModel[…]transfer function model
    AffineStateSpaceModel[…]affine state-space model
    NonlinearStateSpaceModel[…]nonlinear state-space model
    DiscreteInputOutputModel[…]discrete input-output model
  • data is an association of the form <|x1data1,…|>, where xi is a variable in smodel and datai is its corresponding data.
  • pars is a list of tunable parameters in smodel. It can have the following forms:
  • {θ1,…}calibration parameters starting from values in smodel
    {{θ1,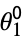},…}calibration parameter θi starting from point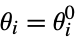
  • spec is an Association that allows the following keys:
  • "SimulationInterval"{tmin,tmax}simulate from time tmin to tmax
    "ParameterValues"{p1val1,…}parameter pi has value vali
    "InitialValues"{x1val1,…}variable xi has initial value vali
    "Inputs"{in1fun1,…}input ini has value funi[t] at time t
    "CalibratedModelName"namename for calibrated SystemModel
    "ExtendModel"Falsewhether the calibrated SystemModel extends smodel
    "Weights"{w1,…}positive multi-objective sum weights wi for each calibration variable in data
  • The "CalibratedModelName" name can have the following forms:
  • Automaticautomatically generate a model name (default)
    "name"name calibrated model "name"
    Noneset calibrated values in place in smodel
  • By default, SystemModelCalibrate[data,smodel,pars,spec] returns a model with parameters set to the calibrated values.
    • Properties
  • SystemModelCalibrate[…,"CalibratedSystemModel"] returns a CalibratedSystemModel object csmodel that can be used to extract additional properties using the form csmodel["prop"].
  • SystemModelCalibrate[…,"prop"] can be used to directly get the value of csmodel["prop"].
  • Typical properties that can be retrieved with SystemModelCalibrate[…,"prop"] include:
  • "CalibratedModel"new model with calibrated parameters
    "CalibratedParameters"parameter estimates
    "ParameterConfidence"parameter confidence information
    "MeanPredictionBandsPlot"mean predictions confidence bands plot with calibration data
    "SinglePredictionBandsPlot"plot of confidence bands based on single observations with calibration data
  • Properties related to data and the calibrated model include:
  • "CalibratedSimulationData"calibrated model simulation results
    "CalibrationData"calibration data in data
    "ValidationData"validation set data
    "CalibratedModelName"model name of new model with calibrated parameters
    "CalibrationDataResponse"response values in the calibration data
    "ValidationDataResponse"response values in the validation data
    "CalibratedDataResponse"calibrated model values for the calibration data
    "CalibratedValidationDataResponse"calibrated model values for the validation data
  • Types of residuals include:
  • "CalibrationDataResiduals"difference between actual and predicted responses
    "ValidationDataResiduals"difference between validation and predicted responses
    "StandardizedResiduals"residuals for calibration data divided by the standard error for each residual
  • Properties of predicted values include:
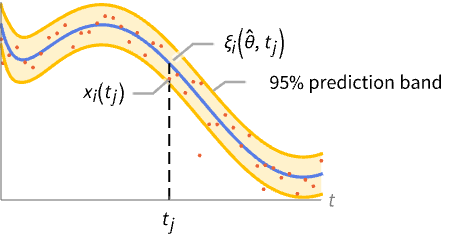
  • "CorrelationMatrix"asymptotic parameter correlation matrix
    "MeanPredictionBands"confidence bands for mean predictions
    "MeanPredictionConfidence"confidence information for the mean predictions of calibration data
    "SinglePredictionBands"confidence bands based on single observations
    "SinglePredictionConfidence"confidence information for the predicted response of single observations of calibration data
  • Properties that measure goodness of calibration include:
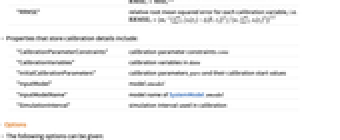
  • "MSE"mean squared error for each calibration variable, i.e.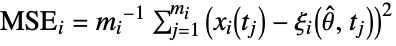
    "RMSE"root mean squared error for each calibration variable, i.e.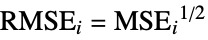
    "RRMSE"relative root mean squared error for each calibration variable, i.e.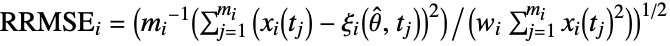
  • Properties that store calibration details include:
  • "CalibrationParameterConstraints"calibration parameter constraints cons
    "CalibrationVariables"calibration variables in data
    "InitialCalibrationParameters"calibration parameters pars and their calibration start values
    "InputModel"model smodel
    "InputModelName"model name of SystemModel smodel
    "SimulationInterval"simulation interval used in calibration
    • Options
  • The following options can be given:
  • ConfidenceLevel 95/100confidence level for parameters and predictions
    FitRegularization Noneregularization for pars
    Method Automaticwhat simulation and calibration methods to use
    NormFunction Normthe norm to minimize
    ProgressReporting $ProgressReportingcontrol display of progress
    ValidationSet Nonevalidation data
    VarianceEstimatorFunction Automaticfunction for estimating the error variance
  • With ConfidenceLevel->p, probability-p confidence intervals are computed for parameter and prediction intervals.
  • FitRegularization and NormFunction can be used to change the calibration target into 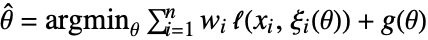, where 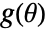is a regularization function, e.g. g(theta)=lambda TemplateBox[{theta, 2}, Norm2]^2 (Tikhonov) or g(theta)=lambda TemplateBox[{theta, 1}, Norm2] (Lasso), and the loss function is given by 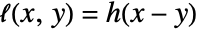, where 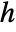is the norm function.
  • The following settings for ValidationSet can be given:
  • Noneuse only the existing calibration data to measure quality (default)
    datavalidation set in the same form as calibration data data
    Scaled[frac]reserve a specified fraction of the calibration data for validation
  • With the setting VarianceEstimatorFunction->f, the common variance is estimated by f[res,w], where res is the list of residuals and w is the list of weights.
  • Method settings take the form Method <|"sub1"val1,…|>.
  • Method suboptions "subi" include:
  • "CalibrationMethod"Automaticcalibration method
    "SimulationMethod"Automaticsimulation method
  • "CalibrationMethod" settings are the same as the Method settings in FindMinimum.
  • "SimulationMethod" settings are the same as the Method settings in SystemModelSimulate.
  • Distributional assumptions are based on an unconstrained model calibrated by minimizing the default loss function.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Use data of the angular velocity of a component to calibrate a model of a hybrid motor:

In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-3iv6cd
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-r3805f

Calibrate the values of the resistance and the damping:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-rzjyw6
Out[4]=4

Simulate with the calibrated parameters and compare with the data:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-k3w12c
Out[5]=5

Use data of an output of a NonlinearStateSpaceModel to calibrate the model:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-j0xe2g
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2o1295

Calibrate a parameter value:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-19wboe
Out[3]=3

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-wbbgxe
Out[4]=4

Scope  (14)Survey of the scope of standard use cases

Data  (3)

Provide data for as many variables as you want to calibrate:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-d02c0m
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-5m2ey7
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-t6qkjs

Calibrate a parameter value:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-nleuck
Out[4]=4

Simulate with the calibrated parameter and compare with the data:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-kfa288
Out[5]=5

Use data with units to calibrate a model of a rocket takeoff:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-3mvvg7
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-vijfda

Calibrate the mass flow rate with data of the mass of the ship:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-6kulr5
Out[3]=3

Use the time-value pairs of a time series as data to calibrate a model:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-w250y3
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2r89d5

Calibrate the values of two parameters:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-ecyn1t
Out[3]=3

Models  (4)

Use data generated with an input signal to calibrate a DiscreteInputOutputModel:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-xyf8te
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-v5shs7
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-quisn8

Specify the input signal to calibrate a parameter value:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-r374t3
Out[4]=4

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-4t0vsk
Out[5]=5

Use data generated with an input signal to calibrate a TransferFunctionModel:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2ptt7b
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-n0i46n
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-j6sj2r

Specify the input signal to calibrate a parameter value:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-9ipp4d
Out[4]=4

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-5ql90f
Out[5]=5

Use data generated with an input signal to calibrate a StateSpaceModel:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-7k0103
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-m6v5lf
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-jwnbl6

Specify the input signal to calibrate parameter values:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-fryyiu
Out[4]=4

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-38nz7n
Out[5]=5

Use data of the output of an AffineStateSpaceModel to calibrate the model:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-eiyqea
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-86t54a

Calibrate a parameter value:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2g7kk8
Out[3]=3

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-zi9hyg
Out[4]=4

Parameters and Constraints  (2)

Indicate initial guess values for the calibration parameters:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-ojuxd2
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-kkb0sa

Calibrate two parameter values:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-0xf3qq
Out[3]=3

Introduce constraints for the calibration parameters:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-wqhb1y
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-ryhqed

Calibrate two parameter values:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-tc2qcr
Out[3]=3

Confidence intervals are computed assuming an unconstrained model:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-4ap6cq
Out[4]=4

Specification  (4)

Specify a model name for the calibrated model:

In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-q8heyn
In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2njjno

Calibrate the value of a parameter, specifying the calibrated model name:

In[6]:=6
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-u3w0f7
Out[6]=6

Create a calibrated model that extends the input model:

In[9]:=9
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-qoehzl
Out[9]=9
In[10]:=10
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-h1j08c
Out[10]=10

Use data generated with an input signal to calibrate a model:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-j6zw42
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-iibyv8
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-88w9vf

Specify the input signal to calibrate parameter values:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-gttizr
Out[4]=4

Specify a fixed value for a parameter to calibrate another:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-png2jn
Out[5]=5

Specify initial values and a simulation interval to calibrate a model:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-2px2v3
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-jf1s8l

Calibrate a parameter value:

In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-so2wrh
Out[3]=3

Provide weights for the calibration of several variables:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-lbr57f
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-jzlwl0
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-s8ihro
In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-eu1l3w

Calibrate a parameter value:

In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-enkjdc
Out[5]=5

Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

In[6]:=6
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-gt3wwt
Out[6]=6

Properties  (1)

Find the list of available properties:

In[1]:=1
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-jl2dcw
In[2]:=2
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-wvg4zu
In[3]:=3
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-z3aq6w
Out[3]//Shallow=3

These can be extracted more conveniently from the CalibratedSystemModel:

In[4]:=4
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-strjjk
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-uji2qi
Out[5]=5

Extract the single prediction bands plot:

In[6]:=6
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-llab68
Out[6]=6

Extract the single prediction bands plot with a custom confidence level:

In[7]:=7
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-wpuslz
Out[7]=7

Extract the single prediction bands plot with a custom variance estimator function:

In[8]:=8
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-9c8xz1
Out[8]=8

Extract the calibrated model and the calibrated parameters:

In[9]:=9
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-ky2psa
Out[9]=9

Extract the single prediction bands:

In[10]:=10
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-8u9t9m

Extract the single prediction bands evaluated at time t:

In[11]:=11
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-5q0r5q

Extract the root mean squared error for each calibration variable:

In[10]:=10
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-ryzr2o
Out[10]=10

Extract the root mean squared error for each calibration variable providing a validation set:

In[11]:=11
✖
https://wolfram.com/xid/0pm4jsqb2sd7v9te-k2uiek
Out[11]=11

Extract parameter confidence information, including estimates, standard errors, confidence intervals,

  • -statistics for parameter estimates
    • , and ‐values for parameter ‐statistics:

    In[12]:=12
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-3c7oa1
    Out[12]=12

    Options  (8)Common values & functionality for each option

    ConfidenceLevel  (1)

    Use data of the states of a model to calibrate a parameter:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-9g7emj
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-8heqvs
    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-ong3v8

    Use the default confidence level:

    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-8f1adu
    Out[4]=4

    Specify a custom confidence level of 0.5:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-vk6jd9
    Out[5]=5

    FitRegularization  (1)

    Use data of an output to calibrate a model:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-n5iujp
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-1j2y7d

    Use a loss function with no regularization to calibrate parameters:

    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-kuxs25
    Out[3]=3

    Use a Lasso regularization to calibrate parameters:

    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-fq0ioz
    Out[4]=4

    Use a Tikhonov regularization to calibrate parameters:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-x7vzvd
    Out[5]=5

    Method  (2)

    Use data of the mass of a ship to calibrate a model of a rocket takeoff:

    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-cyg6fm
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-f6jst5

    Use the default simulation method to calibrate the value of the mass flow rate:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-qhekn
    Out[5]=5

    Calibrate, specifying a number of interpolation points for simulation:

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-04nh7m
    Out[6]=6

    Use data of an output to calibrate a model:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-0bhgh9
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-eljp2w

    Use the default fitting method to calibrate parameters:

    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-3ebyh2
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-z350ne
    Out[4]=4
    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-50zn9v
    Out[5]=5

    Use the conjugate gradient method to calibrate parameters:

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-v8g4d0
    In[7]:=7
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-8kna33
    Out[7]=7
    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-m7d7ms
    Out[8]=8

    NormFunction  (1)

    Use data of an output to calibrate a model:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-y6myny
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-2nu6ps

    Use the default norm in the loss function to calibrate parameters:

    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-wui3jk
    Out[4]=4

    Use the -norm in the loss function to calibrate parameters:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-4ssvba
    Out[5]=5

    Use the 1-norm in the loss function to calibrate parameters

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-qeaquu
    Out[6]=6

    ProgressReporting  (1)

    Use data of the mass of a ship to calibrate a model of a rocket takeoff:

    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-y5oyt2
    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-mioyzt

    Calibrate the value of the mass flow rate with the default progress reporting:

    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-j4tcji
    Out[8]=8

    Calibrate without progress reporting:

    In[9]:=9
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-xf166n
    Out[9]=9

    ValidationSet  (1)

    Use data of an output to calibrate a model:

    In[16]:=16
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-eq65we
    In[20]:=20
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-18nqca

    Calibrate parameters using no validation data:

    In[21]:=21
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-uvbgxw
    Out[21]=21

    Calibrate parameters by reserving a fraction of the calibration data for validation:

    In[22]:=22
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-ipbi82
    Out[22]=22

    Use a particular random seed in the selection of validation data to ensure predictable results:

    In[31]:=31
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-m05dwl
    Out[31]=31

    Use a custom validation set to calibrate parameters:

    In[11]:=11
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-iuarji
    Out[11]=11

    VarianceEstimatorFunction  (1)

    Use data of the states of a model to calibrate a parameter:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-1gl47d
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-wk2koz
    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-ygs3cb

    Use the default estimate of error variance:

    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-rkdx3e
    Out[4]=4

    Estimate the variance by the mean absolute error:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-0dzyyl
    Out[5]=5

    Applications  (5)Sample problems that can be solved with this function

    Closed-Flow Heating System  (1)

    Use temperature data to estimate the heat flow rate for a burner in a model of a heating system:

    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-m127o8
    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-pvbbwz
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-eat7h7
    Out[4]=4

    Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-e03gj8
    Out[5]=5

    Plot the residuals against time:

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-x90yaq
    Out[6]=6

    Model Simplification  (1)

    Recreate the behavior of a speaker by calibrating a simpler circuit using simulation results as input data:

    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-m9a08j
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-476uld

    Compare the behavior of both models before calibration:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-bfnq3k
    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-vao1cu
    In[7]:=7
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-2jxg01
    Out[7]=7

    Retrieve simulation results as data and use them for calibration:

    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-qchum6
    In[9]:=9
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-6fuaww
    Out[9]=9

    Compare the calibrated model with the speaker:

    In[10]:=10
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-3k1dgu
    Out[10]=10

    Conveyor Belt Friction  (1)

    Calibrate the viscous contribution to friction in a model of a body held by a spring on top of an accelerating conveyor belt:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-e5k75t

    The total kinetic friction can be modeled as a combination of viscous, Coulomb and Stribeck components:

    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-xphj61
    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-43p80l
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-g51qei
    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-n7usdt

    The equations of motion must include the event-generating effect of the static friction, which holds the body static with respect to the belt until an upper bound is breached by external forces:

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-cjg8da
    In[7]:=7
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-tfmh55

    Set initial values for the position and velocity of the body and the discrete variable tracking the impact of static friction:

    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-cdidji

    Set parameter values and create the system model:

    In[9]:=9
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-n7buob
    In[10]:=10
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-edjini
    Out[10]=10

    Calibrate the contribution of the viscous term with data for the position of the body:

    In[11]:=11
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-pvlxw5
    In[12]:=12
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-6j8sf0
    Out[12]=12

    Find the 95% confidence interval for the viscous friction factor:

    In[13]:=13
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-qz3imv
    Out[13]=13

    Compute the single prediction bands and plot them together with the data and the calibrated simulation response:

    In[14]:=14
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-4gphzh
    Out[14]=14

    Compute the extremes of the position and velocity for the calibrated simulation data:

    In[15]:=15
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-5ftm3v
    Out[15]=15

    Reverse Engineering of Controller  (1)

    Deduce the controller parameters in a controlled system for which you have step response data:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-p2npyj
    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-8tr33u
    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-uaszmg
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-n4llhe

    Connect the plant model to a controller with symbolic parameters:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-piudt7
    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-5xvpbp

    Calibrate the parameters in the model with the step response data of the controlled system:

    In[7]:=7
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-mb8xe5
    Out[7]=7

    Compare the simulation results of the calibrated model with the reverse-engineered model:

    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-560k07
    Out[8]=8

    Reduced Three-Body Problem  (1)

    Estimate the mass of a planet that orbits a star from the trajectory of one of its moons in a reduced three-body planetary system:

    In[1]:=1
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-isu5ag

    The dynamics of the moon are dictated by Newtonian gravity:

    In[2]:=2
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-51p3sk

    Set parameter values for the system and initial values for the trajectory of the moon:

    In[3]:=3
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-owroy
    In[4]:=4
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-vzu211

    Create a model from the equations, parameters and initial values:

    In[5]:=5
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-2g8t52
    Out[5]=5

    Simulate the model before calibration and plot the trajectories of the three bodies:

    In[6]:=6
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-tqiiic
    In[7]:=7
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-si5r1q
    Out[7]=7

    Calibrate a model with data for the trajectory of the moon:

    In[8]:=8
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-3sxxi1
    In[9]:=9
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-ymngjk
    In[10]:=10
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-8jkzqw
    Out[10]=10

    Retrieve the simulation data and plot the trajectories for the calibrated model:

    In[11]:=11
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-h8dqat
    In[12]:=12
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-hbhdur
    Out[12]=12

    Compare the data with the calibrated trajectory:

    In[13]:=13
    ✖
    https://wolfram.com/xid/0pm4jsqb2sd7v9te-3fpy4n
    Out[13]=13
    Wolfram Research (2023), SystemModelCalibrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.
    ✖
    Wolfram Research (2023), SystemModelCalibrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.

    Text

    Wolfram Research (2023), SystemModelCalibrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.

    ✖
    Wolfram Research (2023), SystemModelCalibrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.

    CMS

    Wolfram Language. 2023. "SystemModelCalibrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.

    ✖
    Wolfram Language. 2023. "SystemModelCalibrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelCalibrate.html.

    APA

    Wolfram Language. (2023). SystemModelCalibrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelCalibrate.html

    ✖
    Wolfram Language. (2023). SystemModelCalibrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelCalibrate.html

    BibTeX

    @misc{reference.wolfram_2025_systemmodelcalibrate, author="Wolfram Research", title="{SystemModelCalibrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelCalibrate.html}", note=[Accessed: 29-March-2025 ]}

    ✖
    @misc{reference.wolfram_2025_systemmodelcalibrate, author="Wolfram Research", title="{SystemModelCalibrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelCalibrate.html}", note=[Accessed: 29-March-2025 ]}

    BibLaTeX

    @online{reference.wolfram_2025_systemmodelcalibrate, organization={Wolfram Research}, title={SystemModelCalibrate}, year={2023}, url={https://reference.wolfram.com/language/ref/SystemModelCalibrate.html}, note=[Accessed: 29-March-2025 ]}

    ✖
    @online{reference.wolfram_2025_systemmodelcalibrate, organization={Wolfram Research}, title={SystemModelCalibrate}, year={2023}, url={https://reference.wolfram.com/language/ref/SystemModelCalibrate.html}, note=[Accessed: 29-March-2025 ]}