VarianceGammaPointProcess
VarianceGammaPointProcess[μ,λ,α,β,d]
![]() における,密度 μ,クラスタ平均 λ,形状パラメータ α および β の分散ガンマクラスタ点過程を表す.
における,密度 μ,クラスタ平均 λ,形状パラメータ α および β の分散ガンマクラスタ点過程を表す.
詳細

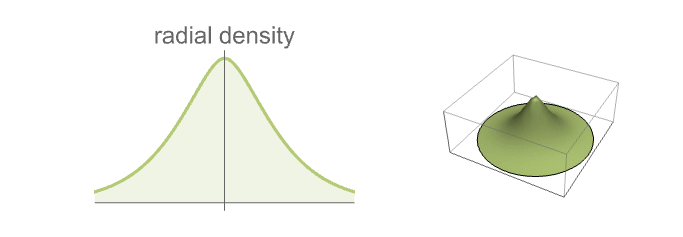
- VarianceGammaPointProcessは,中心が空間全体に均一に分布し,クラスタ点が柔軟な動径分布で等方的に分布しているクラスタ化された点配置をモデル化する.
- 主に,宇宙論や熱帯雨林の木の分布で使われる.
- クラスタの中心は,密度 μ のPoissonPointProcessに従って置かれる.
- クラスタの点の数は,平均 λ のPoissonDistributionに従って分布する.
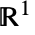 内の各クラスタのクラスタ点はVarianceGammaDistribution[α,
内の各クラスタのクラスタ点はVarianceGammaDistribution[α,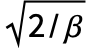 ,0,0]に従って分布する.
,0,0]に従って分布する.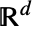 内のクラスタ点はMultinormalDistribution[DiagonalMatrix[{u,u,…}]]に従って分布する.クラスタの中心を中心とするGammaDistribution[α,β]からサンプルとして
内のクラスタ点はMultinormalDistribution[DiagonalMatrix[{u,u,…}]]に従って分布する.クラスタの中心を中心とするGammaDistribution[α,β]からサンプルとして 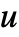 が取られる.
が取られる.- VarianceGammaPointProcessの μ,λ,α,β は任意の正の実数でよく,d は任意の正の整数でよい.
- VarianceGammaPointProcessのためのPointProcessEstimatorには次の設定を使うことができる.
-
"FindClusters" FindClusters関数を使う "MethodOfMoments" 均一測度を使ってパラメータを推定する - VarianceGammaPointProcessは,RipleyK,PointCountDistribution,RandomPointConfiguration等の関数と一緒に使うことができる.

例題
すべて開くすべて閉じる例 (4)
スコープ (2)
RegionEmbeddingDimensionがそのRegionDimensionと等しい任意の有効なRegionQからサンプルを取る:
特性と関係 (5)
PointCountDistributionは既知である:
2Dにおける分散ガンマ点過程についてのRipleyの ![]() 関数とBesagの
関数とBesagの ![]() 関数:
関数:
分散ガンマ点過程のRipleyの ![]() 関数はポアソン点過程よりも大きい:
関数はポアソン点過程よりも大きい:
テキスト
Wolfram Research (2020), VarianceGammaPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html.
CMS
Wolfram Language. 2020. "VarianceGammaPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html.
APA
Wolfram Language. (2020). VarianceGammaPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html