WalleniusHypergeometricDistribution

WalleniusHypergeometricDistribution[n,nsucc,ntot,w]

Walleniusの非心超幾何分布を表す．

詳細

  • Walleniusの超幾何分布は，オッズ比 w で nsucc回の成功を含む大きさが ntotの母集団から依存的に n 回引いた場合の成功回数の分布を与える．
  • Walleniusの超幾何分布における整数値 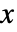の確率はTemplateBox[{{n, _, {(, succ, )}}, x}, Binomial] TemplateBox[{{{n, _, {(, tot, )}}, -, {n, _, {(, succ, )}}}, {n, -, x}}, Binomial] int_0^1(1-t^(1/d))^(n-x) (1-t^(w/d))^xdt に等しい．ただし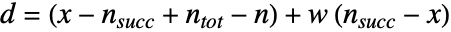，である．
  • WalleniusHypergeometricDistributionでは，n，nsucc，ntotは0<n≤ntotで0≤nsucc≤ntotとなる任意の整数でよく，w は任意の正の実数でよい．
  • WalleniusHypergeometricDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • WalleniusHypergeometricDistribution[n,nsucc,ntot,w]は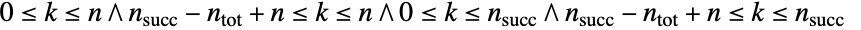，に含まれる整数値 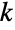について定義され，4つの母数 n，nsucc，ntot，w によって決定された離散統計分布を表す．ここで，w は，Walleniusの超幾何分布によって表される実験のオッズ比を表す実数であり，n，nsucc，ntotは，実験中の抽出回数，母集団中の成功回数，抽出元の母集団の大きさをそれぞれ表す，0<n≤ntotおよび0<nsucc≤ntotを満足する整数である．Walleniusの超幾何分布は離散的で単峰性の確率密度関数(PDF)を持つ．この分布は，（中心）超幾何分布（Wolfram言語中ではHypergeometricDistribution）と区別するために，Walleniusの非心超幾何分布として参照されることがある．
  • Walleniusの超幾何分布は，重みがそれぞれ w1と w2の，nsucc個の青いボールとntot-nsucc個の緑のボールが入った特定の壷のモデルから始まる．特定のボールを抽出する確率は重みに比例し，他のボールに何が起ったかに依存するように，実験前に，固定数の n 個のボールがランダムに取り出される．この構造下では，n で与えられる抽出された青いボールの数をモデル化する条件付きの分布は，w=w1/w2のWalleniusの超幾何分布でモデル化される．このモデルは，FisherHypergeometricDistributionを定義する壷のモデルとほぼ等しい．ただし，後者は，個々の抽出がBinomialDistributionによってモデル化される，独立した取り出し手続きによってモデル化される点が異なる．
  • 現実世界の数多くの現象が，Walleniusの超幾何分布によってモデル化可能である．例えば，この分布は，限られた食料を競い合う種の死亡をモデル化する（種の成員の運命は互いに依存していると仮定する）．Walleniusの超幾何分布は，モンテカルロシミュレーション理論にとっても重要で，偏ったサンプリングの一般化されたモデルであるとみなされている．
  • RandomVariateを使って，Walleniusの超幾何分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,WalleniusHypergeometricDistribution[n,nsucc,ntot,w]]（より簡略すると xWalleniusHypergeometricDistribution[n,nsucc,ntot,w]）を使って，確率変数 x が，Walleniusの超幾何分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[WalleniusHypergeometricDistribution[n,nsucc,ntot,w],x]およびCDF[WalleniusHypergeometricDistribution[n,nsucc,ntot,w],x]を使って得られることがある．PDFの閉形式は存在しないので注意が必要である，平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．これらの数量は，DiscretePlotを使って可視化することができる．
  • DistributionFitTestを使って，与えられたデータ集合がWalleniusの超幾何分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからWalleniusのパラメトリック超幾何分布を推定することが，FindDistributionParametersを使ってデータをWalleniusの超幾何分布にフィットすることができる．ProbabilityPlotを使ってWalleniusの記号超幾何分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使ってWalleniusの記号超幾何分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたWalleniusの超幾何分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってWalleniusの超幾何分布を含む高次元分布を構築することが，ProductDistributionを使ってWalleniusの超幾何分布を含む独立成分分布の結合分布を計算することができる．
  • WalleniusHypergeometricDistributionは数多くの他の統計分布と関係がある．先述した通り，WalleniusHypergeometricDistribution，FisherHypergeometricDistribution，HypergeometricDistributionの間には基本的な繋がりがある，後者の関係は，FisherHypergeometricDistribution[n,nsucc,ntot,1]がHypergeometricDistribution[n,nsucc,ntot]と同じPDFを持つことに注意を払うことで，数量的に正確にできる．

例題

すべて開くすべて閉じる

例  (4)

確率質量関数：

累積分布関数：

平均は閉形式を持たないが，数値的に求めることができる：

分散は閉形式を持たないが，数値的に求めることができる：

スコープ  (4)

超幾何分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

ハザード関数：

分位関数：

アプリケーション  (3)

WalleniusHypergeometricDistributionの累積分布関数は右連続関数の例である：

重み の 個の赤いボールと重み の 個の青いボールの入った壷がある． 個のボールを1つずつ取り出したとき，特定のボールを取り出す確率はその時点で壷に残っているすべてのボールの重み総計の比に等しい．，，，，として赤いボールを取り出す数の分布を求める：

少なくとも3個の赤いボールを取り出す確率を求める：

赤いボールの平均数を求める：

12個のボールを取り出すことを連続して30回行った場合の赤いボールの数のシミュレーションを行う：

WalleniusHypergeometricDistributionに通じる壷のサンプリングはRandomSampleでシミュレーションできる：

特性と関係  (2)

他の分布との関係：

HypergeometricDistributionはWallenius非心超幾何分布の特殊ケースである：

Wolfram Research (2010), WalleniusHypergeometricDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html.

テキスト

Wolfram Research (2010), WalleniusHypergeometricDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html.

CMS

Wolfram Language. 2010. "WalleniusHypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html.

APA

Wolfram Language. (2010). WalleniusHypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html

BibTeX

@misc{reference.wolfram_2024_walleniushypergeometricdistribution, author="Wolfram Research", title="{WalleniusHypergeometricDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_walleniushypergeometricdistribution, organization={Wolfram Research}, title={WalleniusHypergeometricDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/WalleniusHypergeometricDistribution.html}, note=[Accessed: 22-November-2024 ]}