Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

WalleniusHypergeometricDistribution

WalleniusHypergeometricDistribution[n,n_succ,n_tot,w]

表示一个 Wallenius 非中心超几何分布.

更多信息

Wallenius 超几何分布给出从大小为 n_tot、成功次数为 n_succ、优势比为 w 的总体中，进行 n 次独立抽样取得的成功次数的分布.
Wallenius 超几何分布中整数值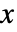的概率等同于 $TemplateBox[{{n, _, {(, succ, )}}, x}, Binomial] TemplateBox[{{{n, _, {(, tot, )}}, -, {n, _, {(, succ, )}}}, {n, -, x}}, Binomial] int_0^1(1-t^(1/d))^(n-x) (1-t^(w/d))^xdt$ ，其中 .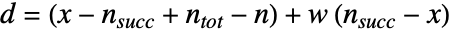
WalleniusHypergeometricDistribution 允许 n、n_succ 和 n_tot 为任何满足 0<n≤n_tot 和 0≤n_succ≤n_tot 的整数，w 为任意正实数.
WalleniusHypergeometricDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.

背景

WalleniusHypergeometricDistribution[n,n_succ,n_tot,w] 表示离散统计分布，定义域为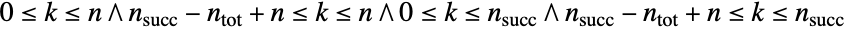所包含的整数值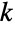，由4个参数 n、n_succ、n_tot 和 w. 这里，w 是一个实数，表示由 Wallenius 超几何分布中描述的试验的胜算比，而 n、n_succ 和 n_tot 为满足 0<n≤n_tot 和 0<n_succ≤n_tot 的整数，分别表示试验的抽样次数，总体的成功次数，和所抽样的总体的大小. Wallenius 超几何分布具有离散且单峰的概率分布函数（PDF）. 该分布有时也被称作 Wallenius 非中心超几何分布，以便与（中心）超几何分布（Wolfram 语言中的 HypergeometricDistribution）区别开来.
Wallenius 超几何分布源自于含有 n_succ 个蓝球和 n_tot-n_succ 个绿球、且重量分别为 w₁ 和 w₂ 的瓮模型. 在试验开始前，固定数目的 n 个球被随机抽取，使取得一个特定球的概率与它的重量成正比，并与其它球的状况相关. 在这种构造下，模拟从 n 个球中取出蓝球的数目的条件分布是通过 Wallenius 超几何分布，其中 w=w₁/w₂. （注意该模型与定义 FisherHypergeometricDistribution 的瓮模型几乎完全相同，不同之处在于，后者采取的是独立抽取步骤，以使每个单独的抽取是通过 BinomialDistribution 模拟.）
许多真实世界的现象都可以使用 Wallenius 超几何分布进行建模. 例如，已经表明该分布可以模拟争夺有限食物资源的物种的死亡（假设物种成员的命运取决于彼此）. Wallenius 超几何分布对于蒙特卡罗模拟理论也很重要，被认为是有偏采样的广义模型.
RandomVariate 可用于给出一个或多个机器精度或任意精度（后者通过 WorkingPrecision 选项）的 Wallenius 超几何分布的伪随机变元. Distributed[x,WalleniusHypergeometricDistribution[n,n_succ,n_tot,w]]，更简洁的表示为 xWalleniusHypergeometricDistribution[n,n_succ,n_tot,w]，可用于声明随机变量 x 服从 Wallenius 超几何分布. 然后这类声明可用于诸如 Probability、NProbability、Expectation 和 NExpectation 等函数中.
概率密度和累积分布函数可以通过使用 PDF[WalleniusHypergeometricDistribution[n,n_succ,n_tot,w],x] 和CDF[WalleniusHypergeometricDistribution[n,n_succ,n_tot,w],x] 给出，但应注意的是它的 PDF 无解析形式的表达式. 均值、中位数、方差、原始矩和中心矩可以分别使用 Mean、Median、Variance、Moment 和 CentralMoment 计算.
DistributionFitTest 可用于检验给定的数据集是否与 Wallenius 超几何分布相一致，EstimatedDistribution 可用于通过给定数据估计 Wallenius 超几何分布参数分布，而FindDistributionParameters 可用于将数据拟合为 Wallenius 超几何分布. ProbabilityPlot 可用于生成已知数据相对于符号式 Wallenius 超几何分布的 CDF 图形，而QuantilePlot 可用于生成已知数据相对于符号式 Wallenius 超几何分布的分位数的分位数图形.
TransformedDistribution 可用于表示 Wallenius 超几何分布的变换，CensoredDistribution 可用于表示在上限和下限值之间删失值的分布，TruncatedDistribution 可用于表示在上限和下限值之间截断值的分布. CopulaDistribution 可用于构建包含 Wallenius 超几何分布的更高维分布，而 ProductDistribution 可用于计算独立分量分布涉及 Wallenius 超几何分布的联合分布.
WalleniusHypergeometricDistribution 与若干其他统计分布相关. 如前所述，在 WalleniusHypergeometricDistribution、FisherHypergeometricDistribution 和 HypergeometricDistribution 之间有重要的关联. 注意到FisherHypergeometricDistribution[n,n_succ,n_tot,1] 具有与HypergeometricDistribution[n,n_succ,n_tot] 相同的 PDF，后者的关系可以精确地量化.

范例

打开所有单元关闭所有单元

基本范例 (4)

概率质量函数：

累积分布函数：

均值没有相应的解析式，但可以通过数值方法求解：

方差没有相应的解析式表示，但可以通过数值方法求解：

范围 (4)

生成服从非中心超几何分布的伪随机数样本：

比较其直方图与概率密度函数：

分布参数估计：

从样本数据中估计一个分布参数:

比较样本的密度直方图和估计分布的概率密度函数：

风险函数：

分位数函数：

应用 (3)

WalleniusHypergeometricDistribution 的累积分布函数是右连续函数的一个例子：

一个盒子里装有重量为的红球个，重量为的蓝球个. 逐个取出个球，取出一个特定球的概率等于该球占当时盒子里剩余球的总重量的比率. 如果，，，，，求得到红球的次数的分布：

求至少得到3次红球的概率：

求红球数量的均值：

模拟30个连续样本中的红球数量，每个样本有12个球：

瓮中取样导致 WalleniusHypergeometricDistribution 可以使用 RandomSample 模拟：

属性和关系 (2)

与其它分布的关系：

HypergeometricDistribution 是非中心超几何分布的一个特例：

顶部