WaveletScalogram
✖
WaveletScalogram
詳細とオプション

- WaveletScalogramは変換係数を彩色された長方形の行としてプロットする.このプロットでは,絶対値が大きいものは暗く表示され,続く各行は異なるウェーブレット指標指定に対応する.
- ウェーブレット指標指定 wind はDiscreteWaveletDataやContinuousWaveletDataで使われているのと同じである.
- WaveletScalogram[wd]はWaveletScalogram[wd,Automatic]に等しい.
- func に使用可能な特別の値
-
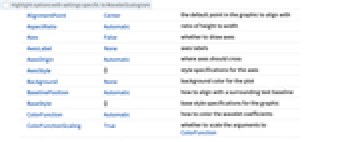
"AbsoluteGlobal" 最大係数で割った絶対値 "AbsoluteLevel" 最大レベル係数で割った絶対値 - WaveletScalogramにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
ColorFunction Automatic ウェーブレット係数の彩色方法 ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか - WaveletScalogramはGraphicsオブジェクトを返す.
全オプションのリスト


例題
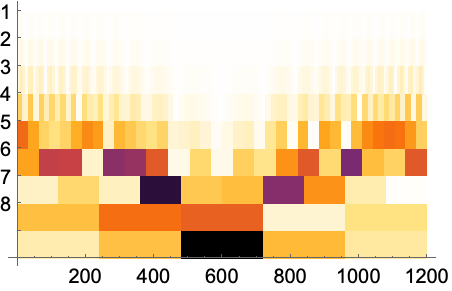
すべて開くすべて閉じる例 (2)基本的な使用例
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-i2g9l8
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-65slt8
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-frjb6m
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-wahzs2
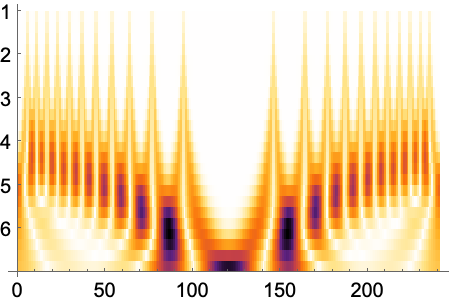
スコープ (10)標準的な使用例のスコープの概要
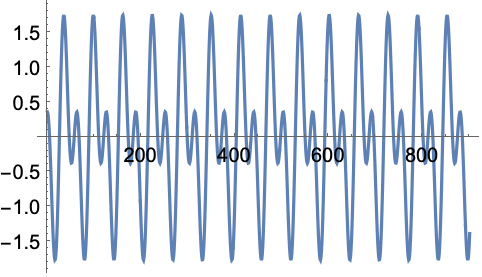
DiscreteWaveletData (6)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-xl09c9
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-0z0dot
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-9gjybd
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-0swvkl
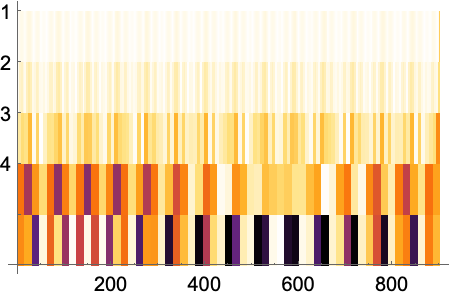
Full目盛を使って垂直軸のラベルを拡張する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-s6hcmo
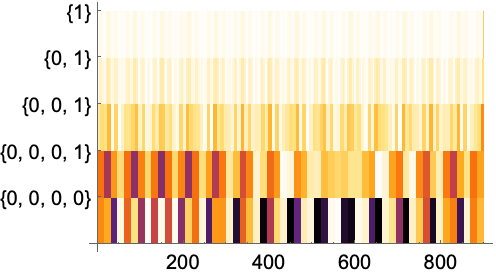
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-oqkap7
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-bc7ip4
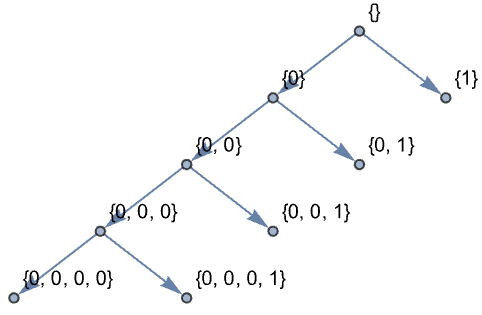
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-hpy7u8
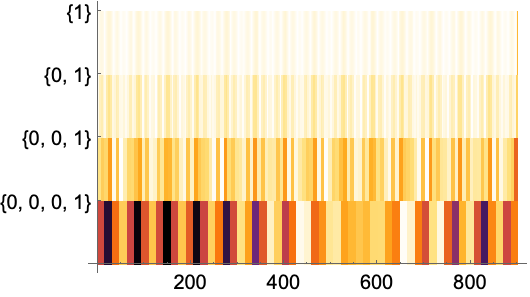
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-dhvpj0
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-w1u9
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-x15ug4
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-0y8p2m
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-pthwbl
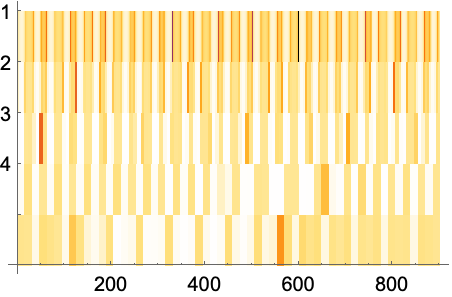
暗い色は係数が大きいことを,明るい色は係数が小さいことを示す:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ojhx2a
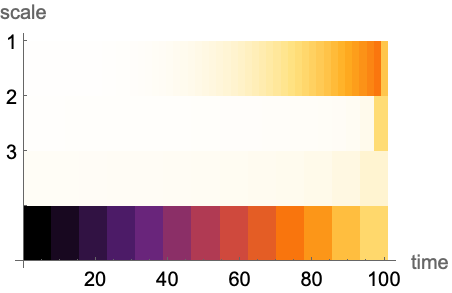
WaveletListPlotを使ってスカログラムを補間する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-3vo864
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-hkvfll
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-e0gp4o
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-xxwplk
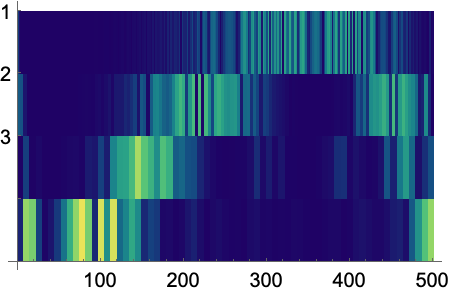
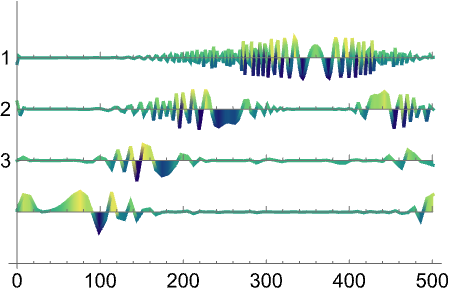
スカログラム中の色のバリエーションはWaveletListPlotを使うとより分かりやすく可視化できる:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-vnswnt
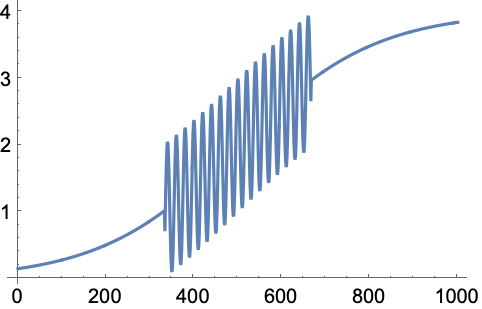
WaveletScalogramは任意の変換から生成されるDiscreteWaveletDataに使うことができる:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-lap1vj
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-dsb81b
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-shsz7b
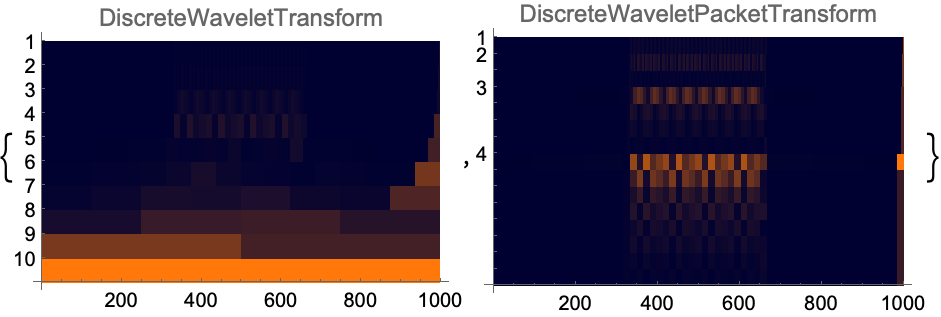
DiscreteWaveletTransformとDiscreteWaveletPacketTransformのスカログラムをプロットする:

https://wolfram.com/xid/0nx7gz2t7ch1y1emq-0jyyxn
StationaryWaveletTransformとStationaryWaveletPacketTransformのスカログラムをプロットする:

https://wolfram.com/xid/0nx7gz2t7ch1y1emq-bs9lt4
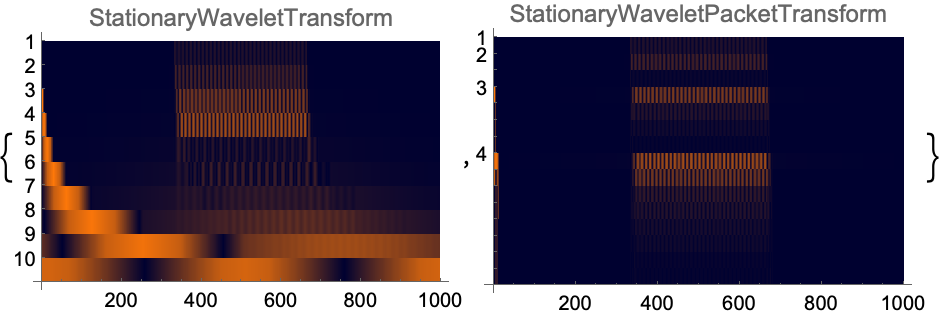
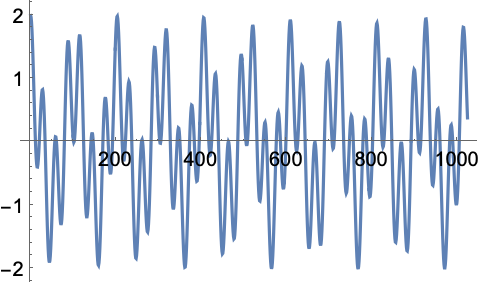
ContinuousWaveletData (4)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-slpoum
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-nkxetu
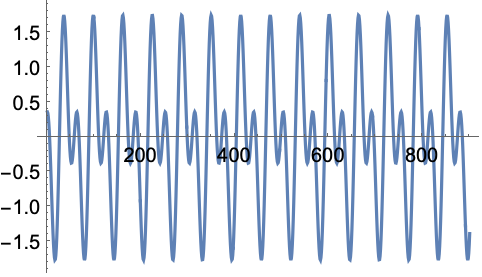
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-rfo5hd
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-j2kktu
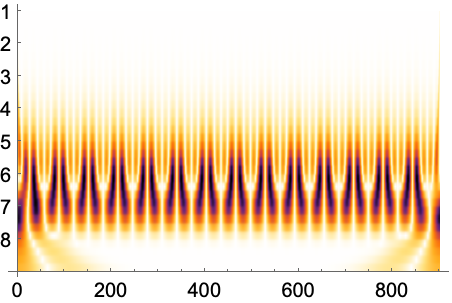
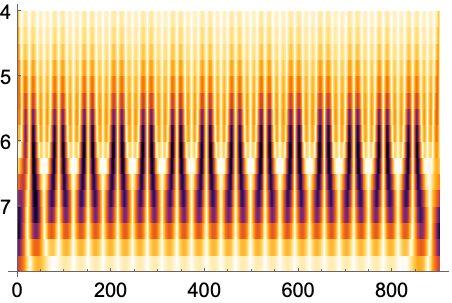
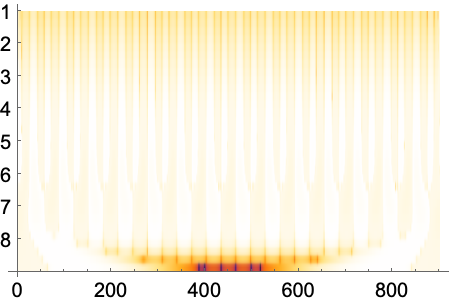
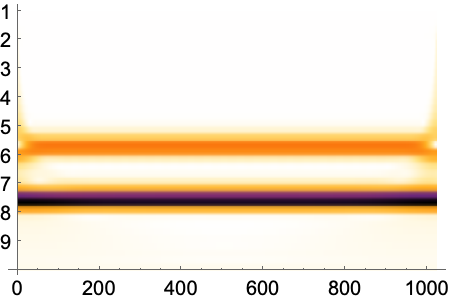
Full目盛を使って垂直軸のラベルを拡大する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-vpivwn
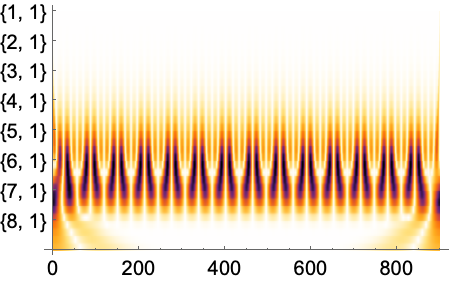
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-9ld14z
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-4ow8qn
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-xkckx6
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-069nkx
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-kojsnt
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-m3935v
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-25tdei
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-gcigct
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ds9q3j
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-cl2bnf
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-fui0pa
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-pxq5p
オプション (18)各オプションの一般的な値と機能
AxesOrigin (2)
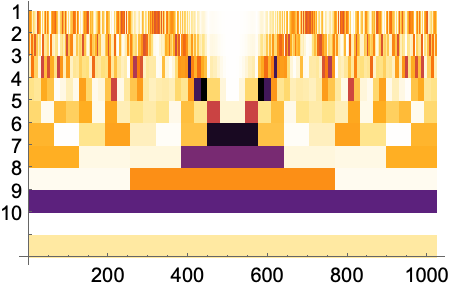
AxesOriginのAutomatic設定は{0,0}に設定されている:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-3uulro
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-8jjy2x
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-8w5orp
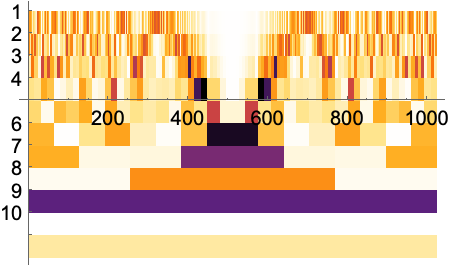
軸の原点を ![]() と
と ![]() にする.これは,5番目の細分化レベルに示されている:
にする.これは,5番目の細分化レベルに示されている:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-r6rwfx
ColorFunction (3)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-nklegw
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-3vzisf
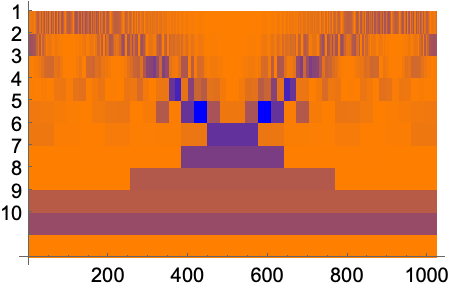
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-uvpzf4
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-82hf91
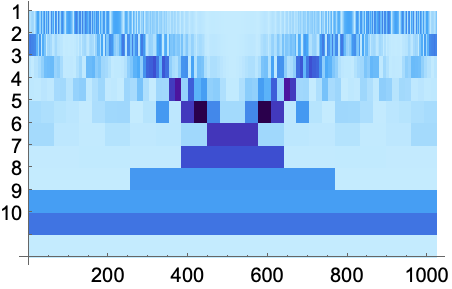
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-icx2et
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-4ofrk5
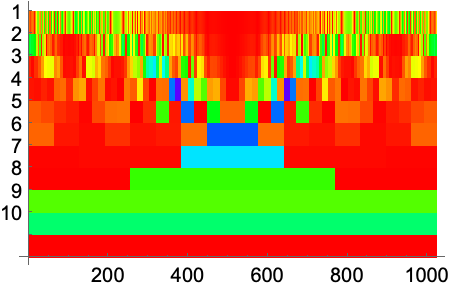
ColorFunctionScaling (2)
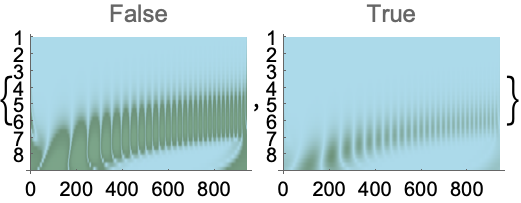
左では引数によるスケーリングは行われていない.右は自動スケーリング:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-l8bzu7
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-dv03l6
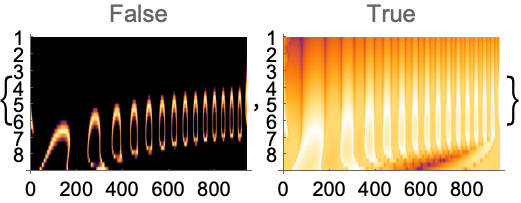
ColorFunctionをより広い幅で使うためにはColorFunctionScalingをFalseにする:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ct2iro
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-pg51va
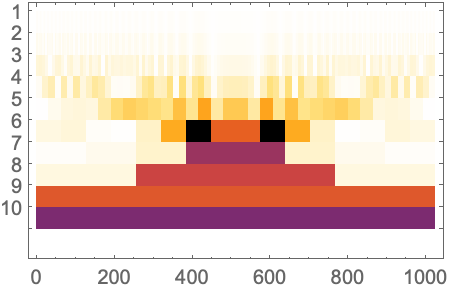
Frame (3)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ow7psf
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-wqpkg7
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-2r4zy0
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-fn8vws

https://wolfram.com/xid/0nx7gz2t7ch1y1emq-qf35vh
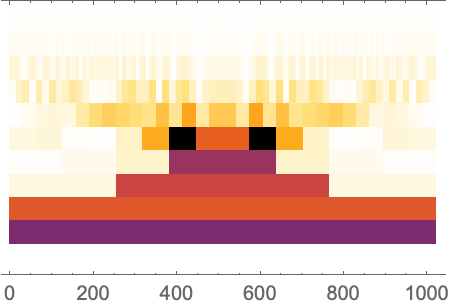
枠,枠目盛,枠目盛ラベルを含む全体的な枠のスタイルを指定する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-y3do4k
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-zbbsqq
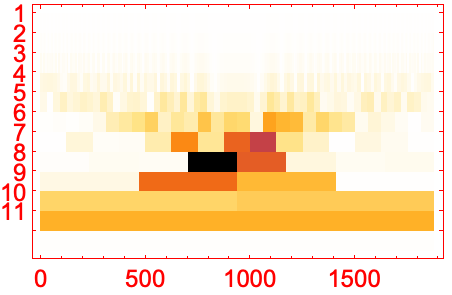
FrameTicks (3)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-n72qc1
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-2o4e4p
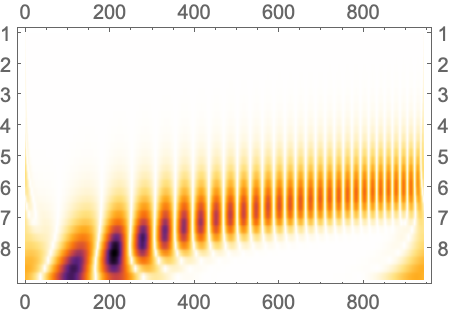
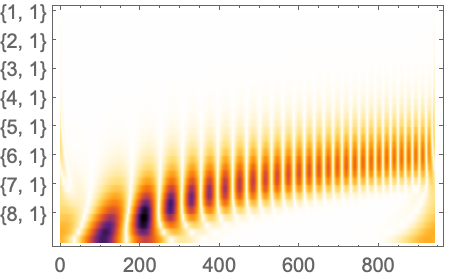
Full目盛を使ってオクターブと音{oct,voc}を示すラベルを垂直軸に描く:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-f45v2f
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-yhe74x
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-c0acpj
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-y4xr3p
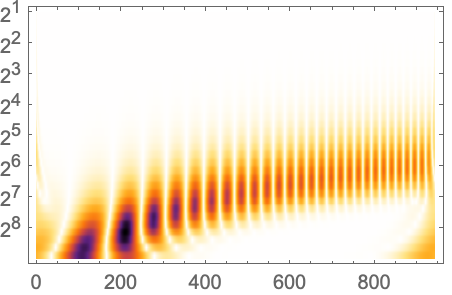
FrameTicksStyleを使って枠目盛ラベルを含む全体的な枠目盛のスタイルを指定する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-1j98a
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-mehvku
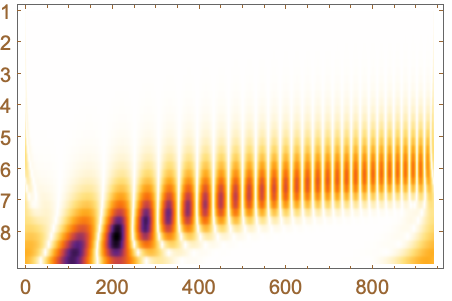
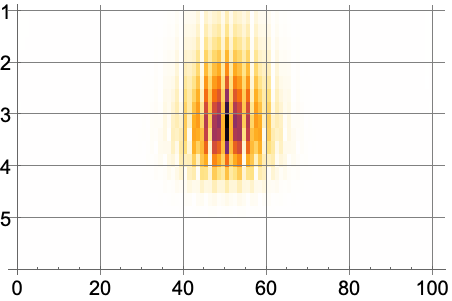
GridLines (3)
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-8nh1jl
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-l02se3
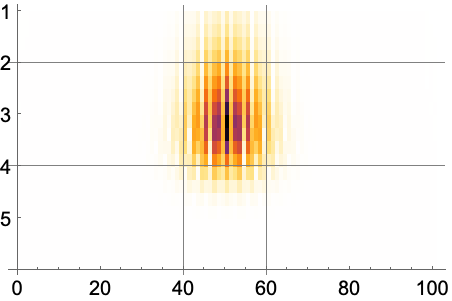
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-fdqf12
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-romp9x
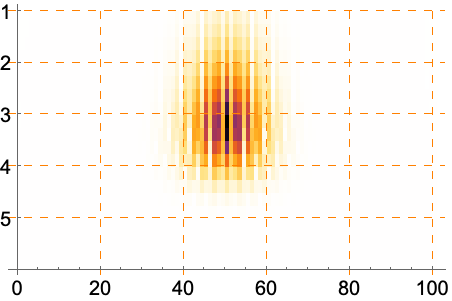
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-c4gkev
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ebniok
Method (2)
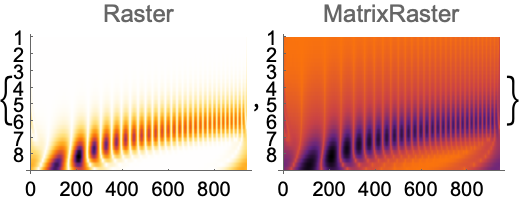
MatrixPlotに使われているような非線形ラスタ関数を使う:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-4ntrqd
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-61egil
DiscreteWaveletDataのウェーブレット係数を反転させる:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-ymo37l
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-yxndgr
アプリケーション (2)この関数で解くことのできる問題の例
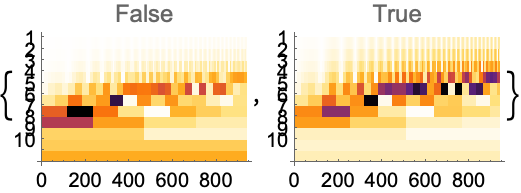
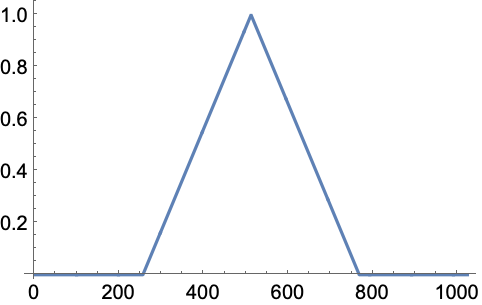
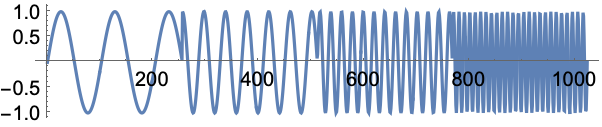
WaveletScalogramを使って不連続性を可視化することができる:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-i2926z
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-xndaw6
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-vobk7q
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-mtt4yw
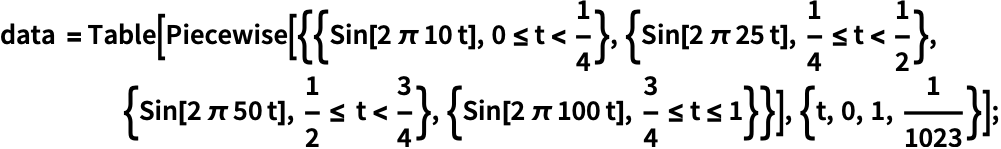
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-734ufp
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-86ww3j
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-le0m15
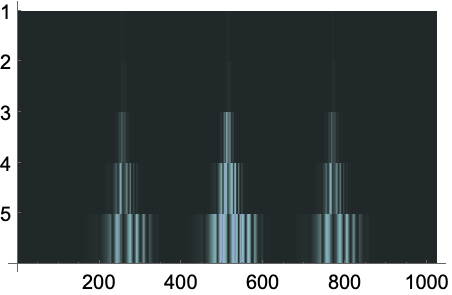
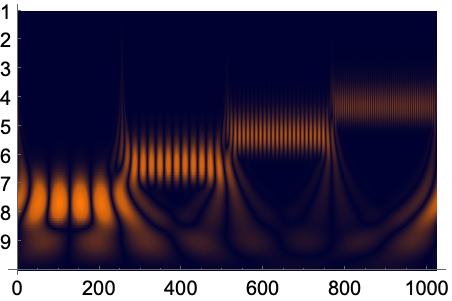
高い周波数は低いオクターブで分解され,低い周波数は高いオクターブで分解される:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-0jcl1q
特性と関係 (2)この関数の特性および他の関数との関係
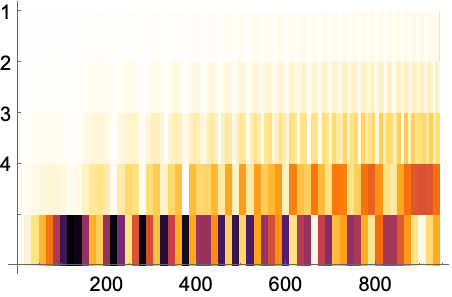
Ticks->Automaticは垂直軸でDiscreteWaveletDataの細分化レベルを示す:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-or2ah8
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-xj14yo
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-bsfd6f
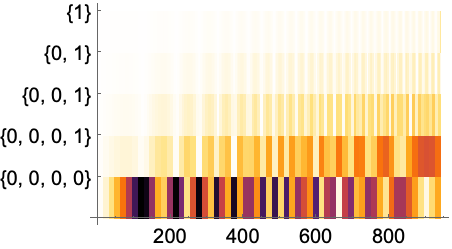
Ticks->Automaticは垂直軸でContinuousWaveletDataの細分化レベルを示す:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-qnvpnl
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-c8mbvs
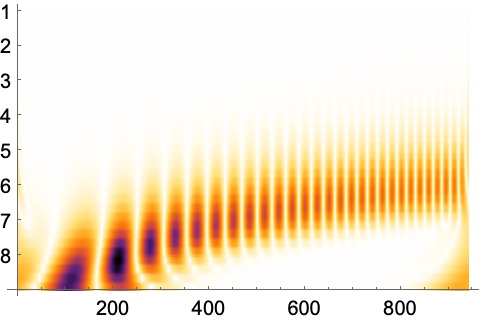
Ticks->Fullはウェーブレットのオクターブと音指定を示す:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-czhhw9
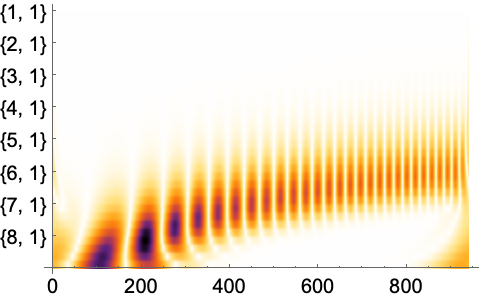
おもしろい例題 (2)驚くような使用例や興味深い使用例
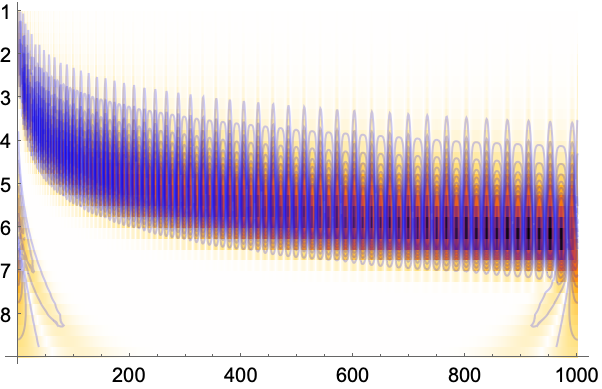
WaveletScalogramの上に等高線を描く:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-c37rr
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-d72t2c
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-le5oib
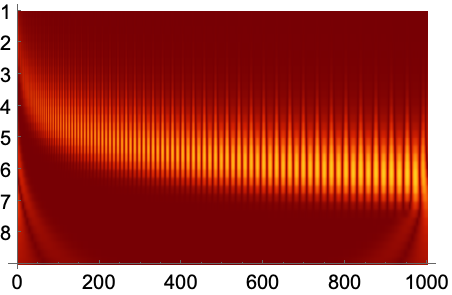
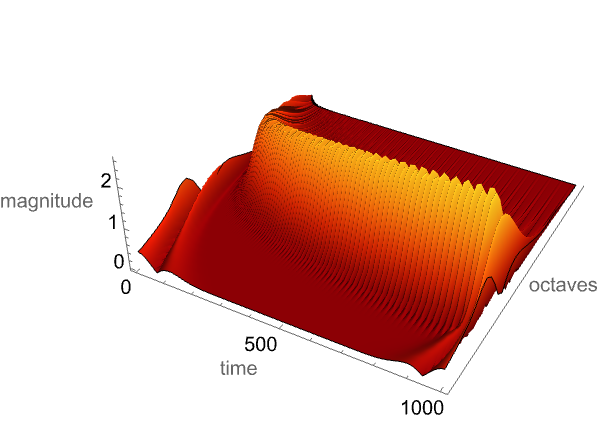
ListPlot3Dを使って三次元空間でウェーブレットスカログラムを可視化する:
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-567p93
https://wolfram.com/xid/0nx7gz2t7ch1y1emq-52bhup

https://wolfram.com/xid/0nx7gz2t7ch1y1emq-4jpkzt
Wolfram Research (2010), WaveletScalogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/WaveletScalogram.html.テキスト
Wolfram Research (2010), WaveletScalogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/WaveletScalogram.html.
Wolfram Research (2010), WaveletScalogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/WaveletScalogram.html.CMS
Wolfram Language. 2010. "WaveletScalogram." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletScalogram.html.
Wolfram Language. 2010. "WaveletScalogram." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletScalogram.html.APA
Wolfram Language. (2010). WaveletScalogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletScalogram.html
Wolfram Language. (2010). WaveletScalogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletScalogram.htmlBibTeX
@misc{reference.wolfram_2025_waveletscalogram, author="Wolfram Research", title="{WaveletScalogram}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletScalogram.html}", note=[Accessed: 14-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_waveletscalogram, organization={Wolfram Research}, title={WaveletScalogram}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletScalogram.html}, note=[Accessed: 14-April-2025
]}