WhenEvent
詳細とオプション




- NDSolve[eqns,…]では,WhenEvent式は eqns に含まれ,特に区分系あるいは混成系の解の指定の一部であるとみなされる.
- WhenEvent式は,NDSolve,NDSolveValue,ParametricNDSolve,ParametricNDSolveValue,DSolve,DSolveValueで使うことができる.
- 事象は,NDSolveにおける eqns の積分中に
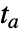 が交差した特定の時点に対応する.
が交差した特定の時点に対応する. - f の根において事象がTrueになるような関数 f によって事象の式が明示的に与えられた場合は,WhenEventは数値によるこん探索法を使って区間
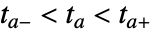 を決定する.ただし,
を決定する.ただし,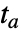 は関数が根を持つ時点である.以下は,明示的に与えられた事象の例である.
は関数が根を持つ時点である.以下は,明示的に与えられた事象の例である. -
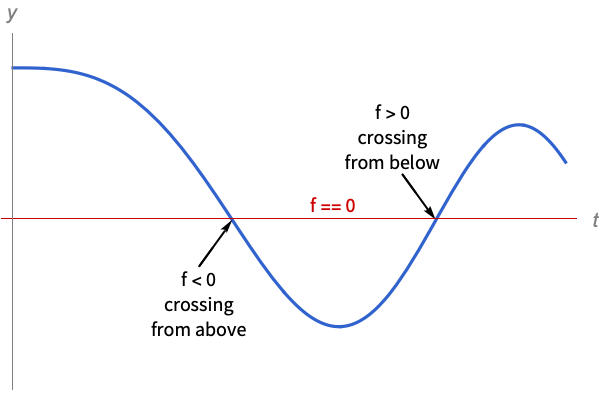
f0 解の変数の関数 f がゼロと交差する f>0 f が下からゼロと交差する f<0 f が上からゼロと交差する Mod[t, 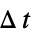 ]0
]0時間変数 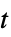 における規則的な区間
における規則的な区間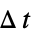 でのサンプル
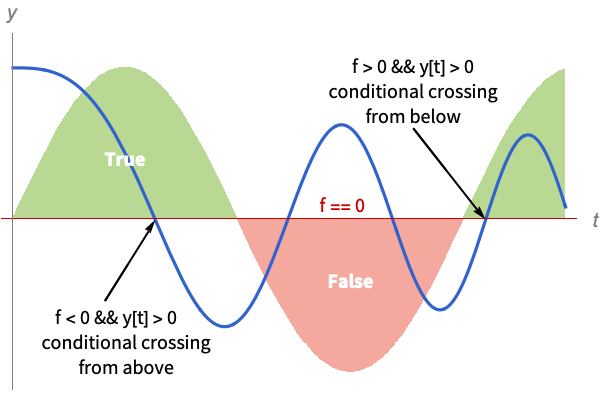
でのサンプル - 明示的な事象の式 ev を使うと,形式 ev && pred を使って述語 pred を条件とする事象が作成できる.この場合,事象は事象関数の根で pred がTrueの場合にのみトリガされる.
- 事象が上記の明示的な形式に直接変換できないような形式で与えられたなら,事象の式はTrueまたはFalseのいずれかの述語 pred であるとみなされる.この場合,区間
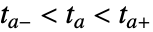 は,二分法を使って求められる.
は,二分法を使って求められる. - 条件を含む明示的な事象と述語とみなされる事象の解釈は多少異なる.明示的な事象は検出される可能性が高く根を求める方がはるかに効率的なので,可能な場合は明示的な事象を使用するのが望ましい. »
- WhenEvent[{event1,…},action]は{WhenEvent[event1,action],…}として扱われる.
- WhenEvent[event,{action1,action2,…}]の場合,アクションは連続的に評価される.
- アクションの評価からの値は,使われるとNDSolveに影響を与えるような特殊な値を持つ場合以外は,WhenEventによって無視される.次の特殊な値が認められる.
-
"StopIntegration" 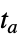 で積分を中止し,解を返す
で積分を中止し,解を返す"RestartIntegration" 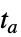 で積分を再開する
で積分を再開する"CrossDiscontinuity" i 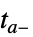 まで積分を行い,外挿して
まで積分を行い,外挿して 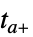 で再開する
で再開する"CrossSlidingDiscontinuity" 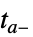 まで積分し,外挿してスライディングモードの条件をチェックし,
まで積分し,外挿してスライディングモードの条件をチェックし,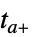 で再開する
で再開する"RemoveEvent" 事象を削除する y[t]->val 状態変数 y を val に変更する d[t]->"DiscontinuitySignature" 不連続のシグナチャ変数 d を変更する - WhenEvent[f==0,d->"DiscontinuitySignature"]のとき,不連続性は曲面 f==0で,d は値{-1, 0, 1}あるいは{-1, 1}を取り,事実上,事象に続く
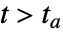 についてはSign[f]に設定される離散変数でなければならない.
についてはSign[f]に設定される離散変数でなければならない. - WhenEventには属性HoldAllがあり,デフォルトで,event と action は変数に近似値が割り当てられたときにのみ評価される.
- WhenEventが取り得るオプション
-
"DetectionMethod" Automatic 事象の検出に使用するメソッド "LocationMethod" Automatic 時間ステップ内で事象を見付けるために使用するメソッド "IntegrateEvent" Automatic 事象関数を積分するかどうか "Priority" Automatic 同時事象の際のアクションの優先順位 - "DetectionMethod"の可能な設定値
-
Automatic 検出メソッドを自動的に決定する "Sign" 符号変換を使う "DerivativeSign" 符号変換と時間導関数を使う "Interpolation" 密な解の出力の補間を使う - "Sign"検出法はオーバーヘッドが最も小さいが,急激に変化する関数内の事象を検出し損なう可能性がある."Interpolation"検出法はより強力で,ステップごとに複数の事象を検出する可能性がある.
- "LocationMethod"の可能な設定値
-
Automatic 位置メソッドは自動的に決定する "StepBegin" ステップの始めに事象を見付ける "StepEnd" ステップの最後に事象を見付ける "LinearInterpolation" ステップ内で線形補間する "Brent" ステップ内でブレント(Brent)の根の位置を使う - "IntegrateEvent"の可能な設定値
-
Automatic 自動的に決定する False 事象関数は積分しない True 事象関数を積分する - "Priority"の設定値は任意の整数またはInfinityである.同時事象の場合,アクションはソートされた優先順で評価される.
例題
すべて開くすべて閉じるスコープ (16)
事象 (6)
いくつかの事象をリストに指定して,そのうちのどれかが起るたびにある事象が引き起こされるようにする:
一般に,事象はTrueになるかどうかの検定が行える任意の式でよい:
停止ボタンが十分早い段階で押されると,積分は ![]() になる前に停止する:
になる前に停止する:
アクション (9)
いくつかのアクションをリストに指定して,順に実行されるようにする:
"StopIntegration"を使って何らかの事象によって解を終了するようにする:
"RemoveEvent"を使って事象を初回の出現後に削除する:
"RestartIntegration"を使って,事象の後で積分を強制的に再開する:
離散状態変数a[t]を使うとこの変更をよりうまく扱うことができる:
規則を使ってDependentVariablesあるいはDiscreteVariablesに変更を加えることができる:
"CrossDiscontinuity"を使って不連続交差を処理する:
"CrossSlidingDiscontinuity"を使ってFilippovの連続性が使えることを示唆する:
DiscreteVariablesと"DiscontinuitySignature"を使って効率的に不連続性を交差する:
ソルバ (1)
DSolveで:
オプション (11)
"DetectionMethod" (3)
"LocationMethod" (3)
"IntegrateEvent" (2)
事象関数が解より速く変化する場合は,交差が見逃されることがある:
![]() から
から ![]() までの事象関数を時間ステップと見付かった交差とともにプロットする:
までの事象関数を時間ステップと見付かった交差とともにプロットする:
"IntegrateEvent"->Trueでは,取られたステップははるかに少ない:
"DetectionMethod"->"Interpolation"では,事象はロバスト性のためにデフォルトで積分される:
アプリケーション (21)
バウンドするボール (3)
最適化 (1)
交差検出 (3)
ハイブリッドの動的な系 (3)
摩擦モデル (1)
摩擦力 ![]() に異なるモデル(粘性,クーロン,ストライベック,静止)を使ってバネで壁に固定され,動いているベルトコンベアーの上に置かれたブロックをモデル化する.モデルごとの位置と速度を比較する:
に異なるモデル(粘性,クーロン,ストライベック,静止)を使ってバネで壁に固定され,動いているベルトコンベアーの上に置かれたブロックをモデル化する.モデルごとの位置と速度を比較する:
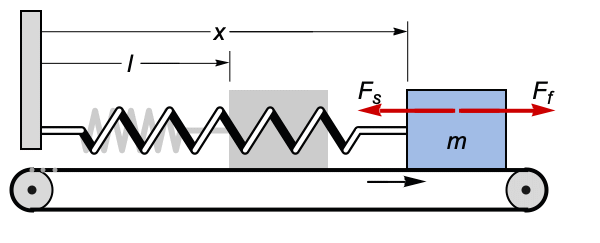
バネの力が十分強くなるまでは,ブロックはベルトとともに動く:
「静止摩擦」はバネの力が値 μ (表面の荒さに依存する)を超えるまでブロックを静止させる.ブロックが動かなくなっている場合は離散変数 stuck を1に設定し,その他の場合はこれを0に設定する:
バネの力が μ より小さいかどうか,またベルトと相対的に見てブロックが動いているかどうかをチェックする:
パワーエレクトロニクス (4)
出力を平滑化するための4個のダイオードとコンデンサを使って,交流から直流への「全波整流器」をモデル化する:
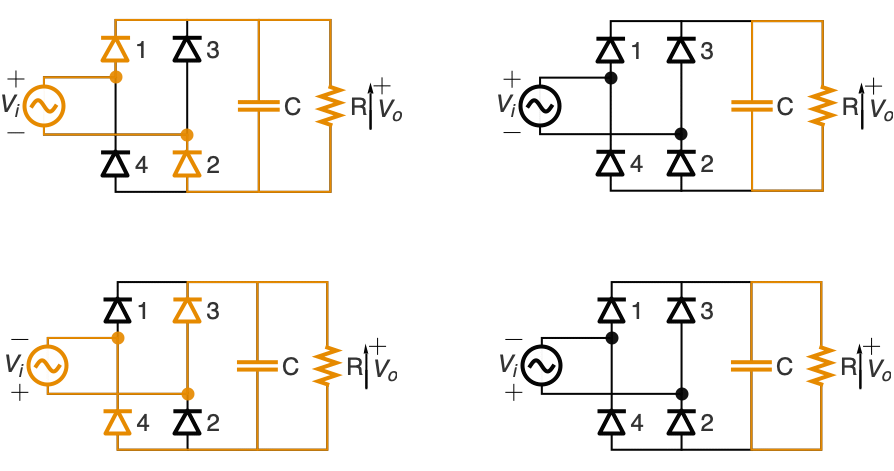
vr が上がって vo[t]=vr[t]になると,コンデンサが充電し,電気機器に電流が流れる.vr が下がり始めると(vr'[t]<0),コンデンサは電気機器を通して放電を始め,出力電圧は vo'[t]=vo[t]/c r に従う:
パルス幅変調フィードバック制御 q[t]を使い,入力電圧レベル vi から所望の出力電圧レベル vd への,直列から直列への「降圧コンバータ」をモデル化する:
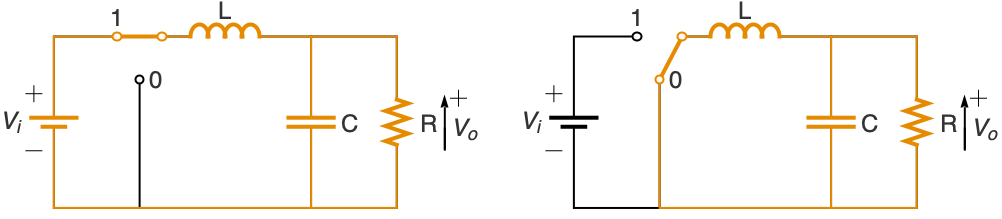
制御信号 q[t]が,各周期 τ の vd/vi の割合でトランジスタをオンにする:
パルス幅変調フィードバック制御 q[t]を使って,入力電圧レベル vi から所望の電圧レベル vd への,直流から直流への「ブーストコンバータ」をモデル化する:
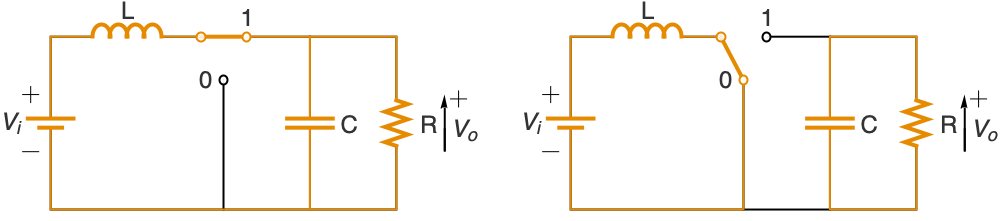
制御信号 q[t]は各周期 τ の vi/vd の割合でトランジスタをオンに切り換える:
パルス幅変調フィードバック制御 q[t]を使って,入力電圧レベル vi から所望の電圧レベル vo への,直流から直流への「バックブーストコンバータ」をモデル化する:
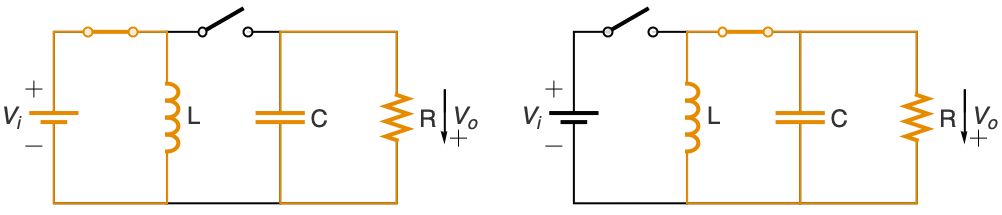
デジタル制御 (5)
離散時間コントローラ ![]() で安定化された系
で安定化された系 ![]() のシミュレーションを行う:
のシミュレーションを行う:
デットビート離散時間コントローラを使って二重積分器を制御する:
サンプルを取った比例微分(PD)コントローラを使って位置を一定に保つ:
状態方程式が ![]() ,
, ![]() で出力が
で出力が ![]() のプラントの離散時間コントローラを設計し,閉ループ系のシミュレーションを行う:
のプラントの離散時間コントローラを設計し,閉ループ系のシミュレーションを行う:
状態推定器と状態フィードバックを使って連続時間コントローラを設計する:
サンプル時間 ![]() でサンプルを取り,離散時間コントローラを得る:
でサンプルを取り,離散時間コントローラを得る:
コントローラとプラントを一緒に使って閉ループ系のシミュレーションを行う:
水平の力fを受けている可動の台車の位置xに角度θで固定された振子をモデル化する:
不安定な垂直の固定点で振子を安定させるためにコントローラを設計する:
WhenEventを使って一定のサンプル時間でフィードバックを適用する:
PDEモデル (1)
部屋の中のサーモスタットで制御された熱発生をモデル化する.部屋の三方の壁は断熱されており,一方は外気温の影響を受けるガラスになっている:
PDEは,サークル![]() 内での熱の生成,空気を通した熱拡散,そしてガラス窓を通した熱の損失をモデル化する:
内での熱の生成,空気を通した熱拡散,そしてガラス窓を通した熱の損失をモデル化する:
位置![]() にあるサーモスタットがトリガの上または下の温度を計測し,離散変数
にあるサーモスタットがトリガの上または下の温度を計測し,離散変数 ![]() が変化すると,ヒーターのスイッチが入ったり切られたりする:
が変化すると,ヒーターのスイッチが入ったり切られたりする:
初期条件を外気温と等しくしてPDFの時間積分をモニターする:
サーモスタットで計測した温度,外気温,ヒーターのトリガを可視化する.青い背景はヒーターが入っていることを示す:
積分中のステップにかかった時間を調べ,NDSolveValueが事象中に必要に応じてタイムステップサイズをどのように調整したかに注目する:
特性と関係 (2)
考えられる問題 (6)
事象の解釈 (1)
事象の検出 (2)
任意の閉じた事象 (1)
テキスト
Wolfram Research (2012), WhenEvent, Wolfram言語関数, https://reference.wolfram.com/language/ref/WhenEvent.html (2014年に更新).
CMS
Wolfram Language. 2012. "WhenEvent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/WhenEvent.html.
APA
Wolfram Language. (2012). WhenEvent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WhenEvent.html
