WhenEvent
更多信息和选项





- 在 NDSolve[eqns,…] 中,WhenEvent 表达式被包含在 eqns 中,被考虑为解的部分规范,尤其是分段或混合系统.
- WhenEvent 表达式可以用于 NDSolve、NDSolveValue、ParametricNDSolve、ParametricNDSolveValue、DSolve 和 DSolveValue.
- 对应于在 NDSolve 中 eqns 积分时,在特定时间
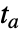 的事件.
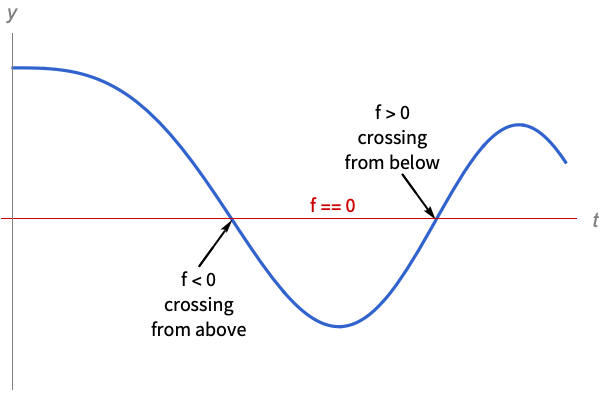
的事件. - 如果事件表达式以解的函数 f 显式给出,例如,在 f 的根处,事件变成 True,那么 WhenEvent 使用查找数值根的过程确定区间
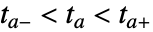 ,其中,
,其中,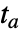 是函数有根的时间. 显式给出事件的范例:
是函数有根的时间. 显式给出事件的范例: -
f0 解的变量函数 f 跨过零 f>0 从下面 f 跨过零 f<0 从上面 f 跨过零 Mod[t, 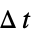 ]0
]0以固定间隔 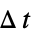 ,时间变量
,时间变量 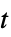 采样
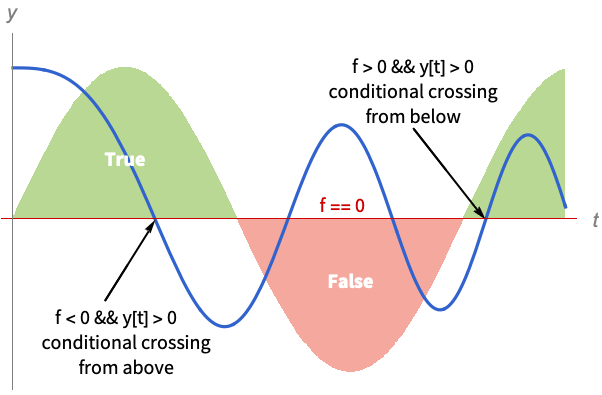
采样 - 如果显式表达式为 ev,事件可以使用形式 ev && pred 以谓词 pred 为条件. 在这种情况下,事件只有在如果 pred 在事件函数的根处为 True 才会被触发.
- 当事件以无法直接转换为上面的显式格式的形式给出,那么事件表达式被考虑为应该是 True 或 False 的谓词 pred. 在这种情况下,使用二等分找到区间
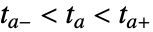 .
. - 带有条件和事件作为谓词的显式事件的诠释略有不同. 如果可能最好使用显式事件,因为它们更有可能被检测到,并能更高效地找到根. »
- WhenEvent[{event1,…},action] 被处理为 {WhenEvent[event1,action],…}.
- 当 WhenEvent[event,{action1,action2,…}] 时,按序计算 action.
- 计算 action 得到的值被 WhenEvent 忽略,除非它有特殊的值被用于影响 NDSolve. 以下特殊值是被确认的:
-
"StopIntegration" 在 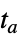 停止积分,返回解
停止积分,返回解"RestartIntegration" 在 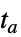 重新开始积分
重新开始积分"CrossDiscontinuity" 积分到 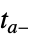 ,推算并在
,推算并在 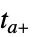 重新开始
重新开始"CrossSlidingDiscontinuity" 积分到 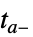 ,推算并检查滑动模式条件,在
,推算并检查滑动模式条件,在 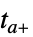 重新开始
重新开始"RemoveEvent" 去除事件 y[t]->val 把状态变量 y 改为 val d[t]->"DiscontinuitySignature" 改变不连续签名变量 d - 当 WhenEvent[f==0,d->"DiscontinuitySignature"] 时,不连续性是曲面 f==0,d 必须是一个接受值 {-1, 0, 1} 或 {-1, 1} 的离散变量,对于
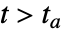 事件后,有效的设为 Sign[f].
事件后,有效的设为 Sign[f]. - WhenEvent 具有属性 HoldAll,因此,默认情况下,event 和 action 只有当变量被赋近似值时才被计算.
- WhenEvent 接受以下选项:
-
"DetectionMethod" Automatic 用于检测事件的方法 "LocationMethod" Automatic 用于在时间步骤中定位事件的方法 "IntegrateEvent" Automatic 是否积分事件函数 "Priority" Automatic 作用于同时发生事件的优先级 - "DetectionMethod" 可能的设置为:
-
Automatic 自动决定检测方法 "Sign" 使用一个符号变换 "DerivativeSign" 使用符号变换和时间导数 "Interpolation" 使用稠密解输出的插值 - "Sign" 检测方法具有最少的开销,但在快速变换的函数中可能错过事件. "Interpolation" 检测方法更强大,在每个步骤中可以检测多个事件.
- "LocationMethod" 可能的设置为:
-
Automatic 自动确定定位方法 "StepBegin" 在每个步骤开始前定位事件 "StepEnd" 在每个步骤结束时定位事件 "LinearInterpolation" 在步骤中线性插值 "Brent" 在一个步骤中使用 Brent 的根定位 - "IntegrateEvent" 可能的设置为:
-
Automatic 自动决定 False 不积分事件函数 True 积分事件函数 - "Priority" 的设置可以为任何整数或 Infinity. 在同时发生的事件中,将按排序的优先级顺序计算 action.
范例
打开所有单元 关闭所有单元范围 (16)
事件 (6)
以列表指定多个事件,当发生任一事件便触发行动(action):
一般而言,事件可以是任何可以被检验为 True 的表达式:
行为 (9)
使用 "StopIntegration" 结束一个事件的解:
在事件第一次发生后,使用 "RemoveEvent" 删除事件:
在事件后,使用 "RestartIntegration" 强迫重新开始积分:
规则可用于修改 DependentVariables 或 DiscreteVariables:
使用 "CrossDiscontinuity" 管理不连续相交点:
使用 "CrossSlidingDiscontinuity" 表明可以使用菲利波夫(Filippov)延续:
使用 DiscreteVariables 和 "DiscontinuitySignature" 有效穿越不连续点:
求解器 (1)
选项 (11)
"DetectionMethod" (3)
"LocationMethod" (3)
"IntegrateEvent"->True 时,步长会取得更小一些:
应用 (21)
混合动力系统 (3)
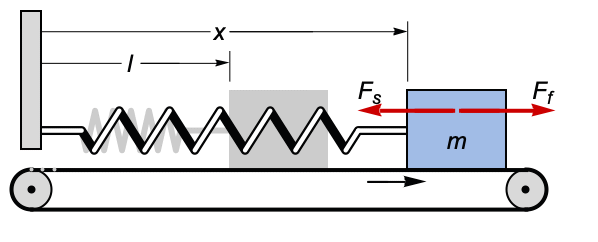
摩擦模型 (1)
电力电子学 (4)
对由四个二极管和一个电容构成的 AC-to-DC 全波整流器建模,用于平滑输出:
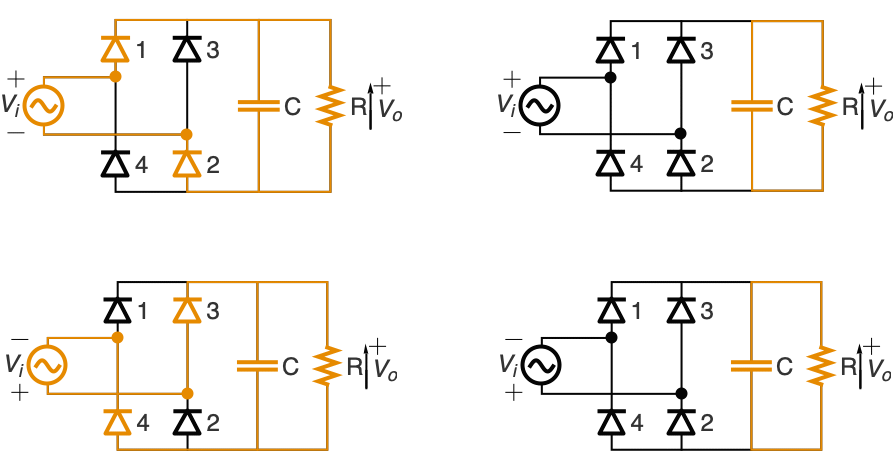
当 vr 增加时,vo[t]=vr[t];电容器充电,并将电流供给到负载. 当 vr 开始降低 (vr'[t]<0),电容器通过负载放电,输出电压服从 vo'[t]=vo[t]/c r :
对使用脉冲宽度调制反馈控制 q[t] 的 DC-to-DC 降压转换器建模,该转换器将输入电压 vi 转换到所需的输出电压 vd:

控制信号 q[t] 将在占每个周期 τ 的 vd/vi 时间段内接通晶体管:
对使用脉冲宽度调制反馈控制 q[t] 的 DC-to-DC 升压转换器建模,该转换器将输入电压 vi 转换到所需的输出电压 vd:
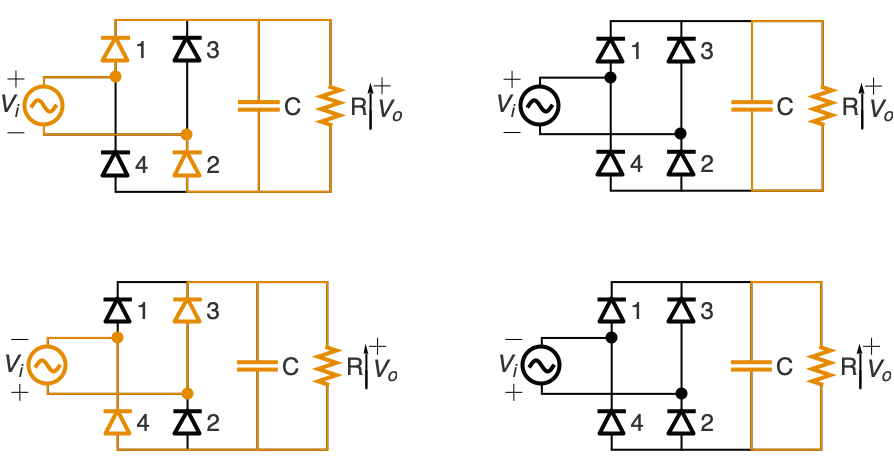
控制信号 q[t] 将在占每个周期 τ 的 vi/vd 时间段内接通晶体管:
对从输入电压电平 vi 到所需输出电压电平 vo 的 DC-to-DC 升压转换器 使用脉冲宽度调制反馈控制 q[t] 建模:
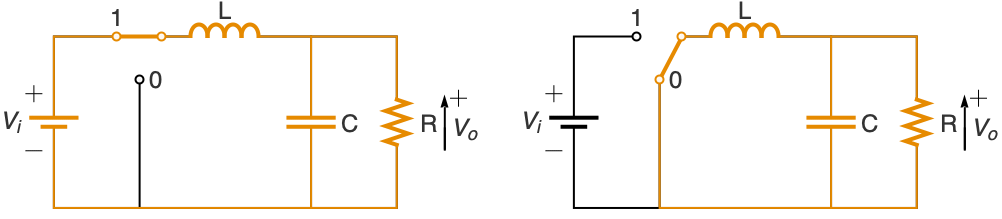
数字控制 (5)
使用无振 (dead-beat) 离散时间控制器控制双重积分器:
设计具有状态方程 ![]() ,
,![]() 和输出
和输出 ![]() 的机械设备(plant)的离散时间控制器,仿真闭环系统:
的机械设备(plant)的离散时间控制器,仿真闭环系统:
模拟一个固定在移动车上位置为 x,角度为 θ,承受水平力为 f 的钟摆:
利用 WhenEvent 在固定采样时间应用反馈:
PDE 模型 (1)
模拟温控器控制下一个房间中的热生成,该房间有三面绝热墙和一面受外界温度影响的玻璃墙:
在事件发生时,加热器的负载会增大或减小. 系数 20 指定过渡的斜率:
注意,up 和 down 阶段有重叠. 这可以防止它们在两种状态之间连续跳转,就像真正的控制器一样.
PDE 模拟空气中的热扩散,在圆 ![]() 内生成热,通过玻璃窗散热:
内生成热,通过玻璃窗散热:
如果位于 ![]() 处的温控器测量到的温度高于/低于触发温度,且离散变量
处的温控器测量到的温度高于/低于触发温度,且离散变量 ![]() 发生变化,则关闭/打开加热器:
发生变化,则关闭/打开加热器:
可视化温控器测量的温度、外部温度和加热器的触发. 加热器处于开启状态时显示蓝色背景:
查看积分过程中的时间步长,注意 NDSolveValue 如何在事件期间根据需要调整时间步长:
属性和关系 (2)
可能存在的问题 (6)
事件诠释 (1)
事件检测 (2)
任意接近事件 (1)
文本
Wolfram Research (2012),WhenEvent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WhenEvent.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "WhenEvent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/WhenEvent.html.
APA
Wolfram 语言. (2012). WhenEvent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WhenEvent.html 年
BibTeX
@misc{reference.wolfram_2025_whenevent, author="Wolfram Research", title="{WhenEvent}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/WhenEvent.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_whenevent, organization={Wolfram Research}, title={WhenEvent}, year={2014}, url={https://reference.wolfram.com/language/ref/WhenEvent.html}, note=[Accessed: 14-February-2026]}