ArcLength
ArcLength[reg]
给出一维区域 reg 的长度.
ArcLength[{x1,…,xn},{t,tmin,tmax}]
给出参数化曲线的长度,其中该参数化曲线的笛卡儿坐标 xi 为 t 的函数.
ArcLength[{x1,…,xn},{t,tmin,tmax},chart]
将 xi 诠释为指定坐标图中的坐标.
更多信息和选项

- ArcLength 也被称作长度或曲线的长度.
- 一维区域可以嵌入任何大于或等于1的维度中.
- 在笛卡尔坐标系中,曲线
 的 ArcLength 是
的 ArcLength 是 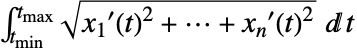 .
. - 在一般的坐标图中,参数化曲线
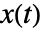 的 ArcLength 由
的 ArcLength 由 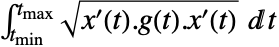 给出,其中
给出,其中 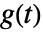 是度量.
是度量. - 在 ArcLength[x,{t,tmin,tmax}] 中,如果 x 是标量,ArcLength 返回参数化曲线 {t,x} 的长度.
- 在 ArcLength 的第三个参数中的坐标图可以用三元组 {coordsys,metric,dim} 的形式指定,就像指定 CoordinateChartData 的第一个参数一样. 可以使用省略 dim 的短形式.
- 可以给出下列选项:
-
AccuracyGoal Infinity 寻求绝对精确度的数字 Assumptions $Assumptions 关于参数所作的假设 GenerateConditions Automatic 是否生成参数条件 PerformanceGoal $PerformanceGoal 尝试优化的性能方面 PrecisionGoal Automatic 寻求精确度的数字 WorkingPrecision Automatic 内部计算所用的精度 - 积分的符号式极限被认为是实数,且是有序的. 符号式坐标图参数的范围被认为由 CoordinateChartData 的 "ParameterRangeAssumptions" 属性给出.
- ArcLength 可与 GeometricScene 的符号区域一起使用.

范例
打开所有单元关闭所有单元范围 (16)
公式区域 (2)
网格区域 (2)
派生区域 (4)
选项 (3)
应用 (8)
根据遍历距离的分数在球面上对 Viviani 曲线进行着色:
计算 Polygon 的周长:
属性和关系 (6)
ArcLength 是一个非负的量:
对于任何一维区域,ArcLength[r] 与 RegionMeasure[r] 相同:
参数形式的 ArcLength 作为积分定义:
ArcLength[x,t,c] 等价于 RegionMeasure[x,{t},c]:
对于一维区域,ArcLength 定义为1在该区域上的积分:
二维区域的周长是其 RegionBoundary 的 ArcLength:
文本
Wolfram Research (2014),ArcLength,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ArcLength.html (更新于 2019 年).
CMS
Wolfram 语言. 2014. "ArcLength." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/ArcLength.html.
APA
Wolfram 语言. (2014). ArcLength. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ArcLength.html 年