ArcLength[reg]
gives the length of the one-dimensional region reg.
ArcLength[{x1,…,xn},{t,tmin,tmax}]
gives the length of the parametrized curve whose Cartesian coordinates xi are functions of t.
ArcLength[{x1,…,xn},{t,tmin,tmax},chart]
interprets the xi as coordinates in the specified coordinate chart.


ArcLength
ArcLength[reg]
gives the length of the one-dimensional region reg.
ArcLength[{x1,…,xn},{t,tmin,tmax}]
gives the length of the parametrized curve whose Cartesian coordinates xi are functions of t.
ArcLength[{x1,…,xn},{t,tmin,tmax},chart]
interprets the xi as coordinates in the specified coordinate chart.
Details and Options

- ArcLength is also known as length or curve length.
- A one-dimensional region can be embedded in any dimension greater than or equal to one.
- The ArcLength of a curve
 in Cartesian coordinates is
in Cartesian coordinates is 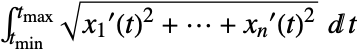 .
. - In a general coordinate chart, the ArcLength of a parametric curve
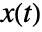 is given by
is given by 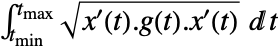 , where
, where 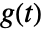 is the metric.
is the metric. - In ArcLength[x,{t,tmin,tmax}], if x is a scalar, ArcLength returns the length of the parametric curve {t,x}.
- Coordinate charts in the third argument of ArcLength can be specified as triples {coordsys,metric,dim} in the same way as in the first argument of CoordinateChartData. The short form in which dim is omitted may be used.
- The following options can be given:
-
AccuracyGoal Infinity digits of absolute accurary sought Assumptions $Assumptions assumptions to make about parameters GenerateConditions Automatic whether to generate conditions on parameters PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PrecisionGoal Automatic digits of precision sought WorkingPrecision Automatic the precision used in internal computations - Symbolic limits of integration are assumed to be real and ordered. Symbolic coordinate chart parameters are assumed to be in range given by the "ParameterRangeAssumptions" property of CoordinateChartData.
- ArcLength can be used with symbolic regions in GeometricScene.

Examples
open all close allBasic Examples (3)
Scope (16)
Special Regions (3)
Formula Regions (2)
The arc length of a circle represented as an ImplicitRegion:
The arc length of a circle represented as a ParametricRegion:
Mesh Regions (2)
Derived Regions (4)
The portion of a circle intersecting a disk:
The arc length of a Circle intersected with a Triangle:
The arc length of a TransformedRegion:
The measure of a RegionBoundary:
Parametric Formulas (5)
An infinite curve in polar coordinates with finite length:
The length of the parabola ![]() between
between ![]() and
and ![]() :
:
Arc length specifying metric, coordinate system, and parameters:
Arc length of a curve in higher-dimensional Euclidean space:
The length of a meridian on the two-sphere expressed in stereographic coordinates:
Options (3)
Assumptions (1)
Applications (8)
The length of a function curve ![]() :
:
Compute the length of Jupiter's orbit in meters:
The length can be computed using the polar representation of an ellipse:
Alternatively, use elliptic coordinates ![]() with half focal distance
with half focal distance ![]() and constant
and constant ![]() :
:
Extract lines from a graphic and compute their coordinate length:
Color a Lissajous curve by distance traversed:
Color Viviani's curve on the sphere by the fraction of distance traversed:
Find mean linear charge density along a circular wire:
Compute the perimeter length of a Polygon:
Properties & Relations (6)
ArcLength is a non-negative quantity:
ArcLength[r] is the same as RegionMeasure[r] for any one-dimensional region:
ArcLength for a parametric form is defined as an integral:
ArcLength[x,t,c] is equivalent to RegionMeasure[x,{t},c]:
For a 1D region, ArcLength is defined as the integral of 1 over that region:
The circumference of a 2D region is the ArcLength of its RegionBoundary:
Related Guides
Text
Wolfram Research (2014), ArcLength, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcLength.html (updated 2019).
CMS
Wolfram Language. 2014. "ArcLength." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/ArcLength.html.
APA
Wolfram Language. (2014). ArcLength. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcLength.html
BibTeX
@misc{reference.wolfram_2025_arclength, author="Wolfram Research", title="{ArcLength}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/ArcLength.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_arclength, organization={Wolfram Research}, title={ArcLength}, year={2019}, url={https://reference.wolfram.com/language/ref/ArcLength.html}, note=[Accessed: 16-January-2026]}