ArcSinDistribution

ArcSinDistribution[{xmin,xmax}]

xminから xmaxまででサポートされている逆正弦分布を表す．

ArcSinDistribution[]

0から1の間でサポートされている逆正弦分布を表す．

詳細

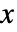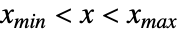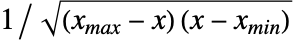  • 逆正弦分布における値 の確率密度は，ではに比例し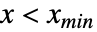，あるいは 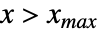では0である．
  • ArcSinDistributionでは，xminと xmaxは xmin<xmaxの任意の実数でよい．
  • ArcSinDistributionでは，xmin と xmax は単位次元が等しい任意の数量でよい． »
  • ArcSinDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • ArcSinDistribution[{xmin,xmax}]は，xminから xmaxまでの値について定義される特定の統計的分布を表す．名前は，その関数形である累積分布関数(CDF)に由来する．これは，正規化された逆正弦関数である．この確率密度関数(PDF)は下に凸であり，領域の中点でその絶対最小値に達し，また中点について鏡映対称となる．また xminおよび xmax双方の近くで特異点（漸近的に無限大に近付く点）を持つ可能性がある．
  • 逆正弦分布は，確率理論や整数論等を含む数多くの数学的文脈で自然に見られる．一次元ウィナー過程の全体的動作の多くは，レヴィによる，いわゆる逆正弦の3法則によって説明することができる．これらの法則は，過程が正である時間の割合，最後に0になった時点，過程が最大に達した時点のすべてが逆正弦分布に従っているとしている．エルデシュによる整数論的結果は，逆正弦分布を指定された整数の小さい素因子数と関連付けている．より最近になって，逆正弦分布は量子コイン投げの確率的モデルの極限分布であることが示された．
  • RandomVariateを使って，逆正弦分布から1つあるいは複数の機械精度あるいは任意精度の（後者はWorkingPrecision オプションによる）擬似乱数変量を与えることができる．Distributed[x,ArcSinDistribution[{xminxmax}]]（より簡略な表記では xArcSinDistribution[{xminxmax}]）を使って，確率変数 x が逆正弦分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で用いることができる．
  • 確率密度関数および累積分布関数は，PDF[ArcSinDistribution[{xmin,xmax}],x]およびCDF[ArcSinDistribution[{xmin,xmax}],x]を使って得ることができる．平均，中央値，分散，原点の周りのモーメント，中心モーメントはそれぞれ，Mean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って与えられたデータ集合が逆正弦分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータから逆正弦パラメトリック分布を推定することが，FindDistributionParametersを使ってデータを逆正弦分布にフィットすることが可能である．ProbabilityPlotを使って記号逆正弦分布のCDFに対する与えられたデータのCDFプロットを生成することができ，QuantilePlotを使って記号逆正弦分布の変位値に対する与えられたデータの変位値プロットを生成することができる．
  • TransformedDistributionを使って変換された逆正弦分布を，CensoredDistributionを使って上限値と下限値の間で打ち切られた値の分布を，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って逆正弦分布を含むより高次元の分布を構築することが，ProductDistributionを使って逆正弦分布を含む独立成分分布との結合分布を計算することができる．
  • 逆正弦分布は多くの他の分布と密接に関係している．例えば，標準逆正弦分布ArcSinDistribution[{0,1}]は，ベータ分布BetaDistribution[1/2,1/2]と厳密に等しい．結果として，ArcSinDistributionはBetaDistributionの多くの関係を継承する．ArcSinDistributionは，同様に，PDF[ArcSinDistribution[{0,1}],x]がPDF[PearsonDistribution[1,1,-1/2,1,-1,0],x]と等しいという意味において，タイプ1のPearsonDistributionであると見ることができる．これは，UniformDistribution，PERTDistribution，ChiSquareDistribution，GammaDistribution，BetaPrimeDistributionとも密接に関係している．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

スコープ  (7)

逆正弦分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

尖度と歪度は一定である：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

記号次数についての閉形式：

FactorialMoment：

Cumulant：

ハザード関数：

分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

平均半径：

アプリケーション  (5)

対称ランダムウォークによる正側滞在時間の割合のシミュレーションを行う：

正側滞在時間の割合を計算する：

極限での比はArcSinDistributionに従う：

標準WienerProcessが正側滞在時間の割合のシミュレーションを行う：

極限での比はArcSinDistributionに従う：

時点0から1の間でWienerProcessの符号が最後に変わった時点の分布を求める：

符号の差を計算して符号の変化を求める：

経路を抽出し，各経路における最後の符号変化の時点を求める：

極限では，時点はArcSinDistributionに従う：

0から1までで，WienerProcessの最大値に対応する時点の分布を求める：

各経路から，その経路の最大値に対応する時点を抽出する：

極限では，この時点はArcSinDistributionに従う：

離散マルコフ連鎖 （ただし，は独立同分布に従う標準一様確率変数で は独立同分布に従う対称ベルヌーイ確率変数の列）は，である任意の初期条件 について定常分布ArcSinDistribution[{0,1}] に収束する：

マルコフ連鎖の実現からサンプルを取り，経路のバーンイン部分を削除する：

マルコフ連鎖からのサンプルは独立ではなく内部構造を示している：

経路の値のヒストグラムとマルコフ連鎖の定常分布のPDFを比較する：

経路の値を使って期待値を近似する：

直角位相値と比較する：

特性と関係  (9)

逆正弦分布は平行移動と正の因子によるスケーリングの下では閉じている：

逆正弦分布の累積分布関数はArcSin関数に比例する：

上での逆正弦分布の平方は上での逆正弦分布になる：

他の分布との関係：

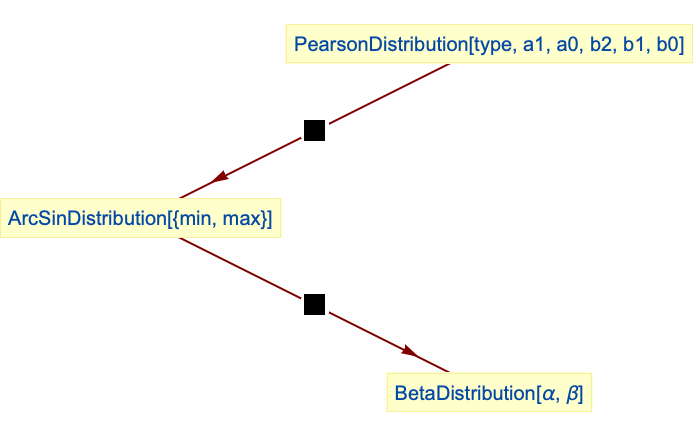
BetaDistributionは逆正弦分布の特別なケースである：

逆正弦分布はタイプ1のPearsonDistributionの特殊な型である：

ArcSinDistributionはUniformDistributionを変換したものである：

ArcSinDistributionはTriangularDistributionを変換したものである：

HoytDistributionはExponentialDistributionとArcSinDistributionから得ることができる：

おもしろい例題  (1)

累積分布関数の等高線を持つ xmax のさまざまな値についての確率密度関数：

Wolfram Research (2010), ArcSinDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcSinDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), ArcSinDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcSinDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "ArcSinDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ArcSinDistribution.html.

APA

Wolfram Language. (2010). ArcSinDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcSinDistribution.html

BibTeX

@misc{reference.wolfram_2024_arcsindistribution, author="Wolfram Research", title="{ArcSinDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ArcSinDistribution.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arcsindistribution, organization={Wolfram Research}, title={ArcSinDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ArcSinDistribution.html}, note=[Accessed: 25-November-2024 ]}