ArgMax
ArgMax[f,x]
给出使 f 最大化的位置 xmax.
ArgMax[f,{x,y,…}]
给出使 f 最大化的位置 {xmax,ymax,…}.
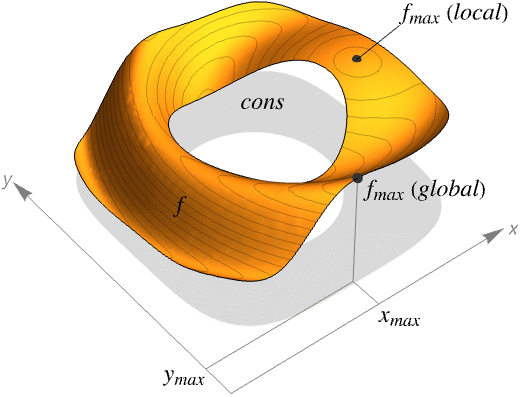
ArgMax[{f,cons},{x,y,…}]
给出使受约束条件 cons 限制的 f 最大化的位置.
ArgMax[…,x∈rdom]
将 x 限制在区域或域 rdom 内.
更多信息和选项
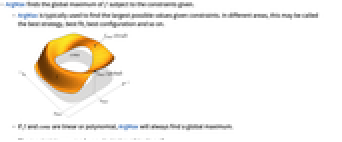

- ArgMax 求给定约束条件限制下 f 的全局最大值.
- ArgMax 通常用于求给定约束条件下可能的最大值. 在不同的领域,这可能被称为最佳策略、最佳方案、最佳配置等.
- 如果 f 和 cons 是线性的或是多项式,ArgMax 总能求出全局最大值.
- 约束条件 cons 可以是以下表达式的任意逻辑组合:
-
lhs==rhs 等式 lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs 不等式 (LessEqual、…) lhsrhs, lhsrhs, lhsrhs, lhsrhs 向量不等式 (VectorLessEqual、…) Exists[…], ForAll[…] 量化条件 {x,y,…}∈rdom 区域或域的指定 - ArgMax[{f,cons},x∈rdom] 实际上等价于 ArgMax[{f,cons∧x∈rdom},x].
- 对于 x∈rdom,可用 Indexed[x,i] 来指代不同的坐标.
- 可能的域 rdom 包括:
-
Reals 实标量变量 Integers 整数标量变量 Vectors[n,dom] 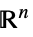 中的向量变量
中的向量变量Matrices[{m,n},dom] 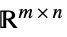 中的矩阵变量
中的矩阵变量ℛ 限制在几何区域 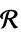 中的向量变量
中的向量变量 - 默认情况下,假定所有变量为实数.
- 如果给定精确输入,ArgMax 将返回精确结果. 如果给定近似输入,它会自动调用 NArgMax.
- 如果最大值只能在极限的位置取得(极限位置超出约束条件所定义的域),或只是渐近地达到,则 ArgMax 将返回最接近极限值的可列举点.
- 即使在多个点达到相同的最大值,也只返回一个.
- 如果无法满足约束条件,ArgMax 会返回 {Indeterminate,Indeterminate,…}.
- N[ArgMax[…]] 调用 NArgMax 来解决不能以符号形式求解的优化问题.
范例
打开所有单元关闭所有单元范围 (36)
基本用法 (7)
单变量问题 (7)
多变量问题 (9)
选项 (1)
WorkingPrecision (1)
如果设置 WorkingPrecision->200,得到的是近似最大值点:
应用 (15)
几何距离 (9)
区域 ℛ 中距给定点 p 最远的点 q 由 ArgMax[{Norm[p-q],q∈ℛ},q] 给出. 求 Disk[] 中距 {1,1} 最远的点:
求标准单位单纯形 Simplex[2] 中距 {1,2} 最远的点:
求标准单位球面 Sphere[] 上距 {1,1,1} 最远的点:
求标准单位单纯形 Simplex[3] 中距 {-1,1,1} 最远的点:
区域 ℛ 的直径是 ℛ 中两点间的最大距离,可以用 ArgMax[Norm[p-q],{q∈ℛ,p∈ℛ}] 来计算. 求 Circle[] 的直径:
求标准单位单纯形 Simplex[2] 的直径:
求标准单位立方体 Cuboid[] 的直径:
可以用 ArgMax[Norm[p-q],{p∈,q∈}] 来找出距离最远的两个点 p∈ 和 q∈. 找出 Disk[{0,0}] 和 Rectangle[{3,3}] 中距离最远的两个点:
几何中心 (3)
如果 ℛ⊆n 是一个全维区域,则切比雪夫中心是使得 -SignedRegionDistance[ℛ,p] 最大化的点 p∈ℛ,即到补区域的距离. 求 Disk[] 的切比雪夫中心:
求 Rectangle[] 的切比雪夫中心:
区域的解析中心由不等式 ℛ=ImplicitRegion[f1[x]≥0∧⋯∧fm[x]≥0,x] 定义,可通过 ArgMax[{Log[f1[x]⋯ fm[x]],x∈ℛ},x] 求出. 求 Triangle[{{0,0},{1,0},{0,1}}] 的解析中心:
求 Cylinder[] 的解析中心:
属性和关系 (4)
Maximize 给出最大值和最大化点:
ArgMax 给出精确的全局最大化点:
NArgMax 试图用数值法求出全局最大化点,但有可能只找到局部最大化点:
FindArgMax 求出取决于起始点的局部最大化点:
如果取不到最大值,ArgMax 可能会给出一个边界上的点:
ArgMax 可以解决线性优化问题:
LinearOptimization 可以通过否定目标来解决相同的问题:
可能存在的问题 (2)
文本
Wolfram Research (2008),ArgMax,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ArgMax.html (更新于 2021 年).
CMS
Wolfram 语言. 2008. "ArgMax." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/ArgMax.html.
APA
Wolfram 语言. (2008). ArgMax. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ArgMax.html 年