BenfordDistribution
基底の母数が b であるBenford分布を表す.
詳細
- BenfordDistributionは最初の桁の分布としても知られている.
- Benford分布における整数値
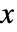 の確率は,
の確率は,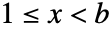 では
では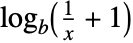 に比例しその他では
に比例しその他では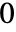 である.
である. - BenfordDistributionでは,
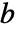 は
は 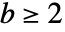 である任意の整数でよい.
である任意の整数でよい. - BenfordDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- BenfordDistribution[b]は,整数値
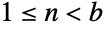 で定義される離散統計分布を表す.ただし,母数 b は
で定義される離散統計分布を表す.ただし,母数 b は 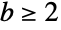 を満足する,基底の母数として知られる整数である.Benford分布は最初の桁の分布として言及されることがある.これは,単調減少値の離散確率密度関数(PDF)を持つ.
を満足する,基底の母数として知られる整数である.Benford分布は最初の桁の分布として言及されることがある.これは,単調減少値の離散確率密度関数(PDF)を持つ. - Benford分布はアメリカ合衆国の物理学者であるFrank Benfordに関係がある.Benfordの名前を冠した「Benfordの法則」(Benfordより50年程前に結果を発表したカナダ系アメリカ人の数学者であるSimon Newcombに敬意を評してNewcomb-Benfordの法則と呼ばれることもある)は,分布の礎石の役割を果たすものである.Benfordの法則は,基底
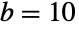 について,現実世界のデータ集合のさまざまなクラスにおける数の最初の桁の数字が1である確率が,(単純に期待されるように),1/9 ≈ 11.1%では与えられず,実際は30%に近いというものである.さらに,数字
について,現実世界のデータ集合のさまざまなクラスにおける数の最初の桁の数字が1である確率が,(単純に期待されるように),1/9 ≈ 11.1%では与えられず,実際は30%に近いというものである.さらに,数字 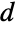 が最初の桁の数字として現れる全体的な確率は,およそ
が最初の桁の数字として現れる全体的な確率は,およそ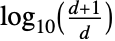 である.(この結果は,対数についての基底の変更式を使って
である.(この結果は,対数についての基底の変更式を使って 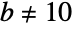 である他の基底にも一般化することができる).Benfordの法則は,物理定数および数学定数,株価,人口,死亡率を含む,数多くの無関係なデータ集合で,経験的に観察されてきた.Benford分布は,複数桁にまたがる値の分布の近似に最もよく使われる.また,第2桁および後ろの桁の数字の観察や,
である他の基底にも一般化することができる).Benfordの法則は,物理定数および数学定数,株価,人口,死亡率を含む,数多くの無関係なデータ集合で,経験的に観察されてきた.Benford分布は,複数桁にまたがる値の分布の近似に最もよく使われる.また,第2桁および後ろの桁の数字の観察や,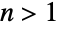 についての
についての 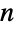 桁の先導配列にまでも敷衍されてきた.
桁の先導配列にまでも敷衍されてきた. - RandomVariateを使ってBenford分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BenfordDistribution[b]](より簡略すると xBenfordDistribution[b])を使って,確率変数 x がBenford分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BenfordDistribution[b],x]およびCDF[BenfordDistribution[b],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がBenford分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからBenfordパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをBenford分布にフィットすることができる.ProbabilityPlotを使って記号Benford分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Benford分布の変位値に対する与えられたデータの変位置のプロットを生成することができる.
- TransformedDistributionを使って変換されたBenford分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってBenford分布を含む高次元分布を構築することが,ProductDistributionを使ってBenford分布を含む独立成分分布の結合分布を計算することができる.
- BenfordDistributionは,ZipfDistributionやParetoDistributionを含む他の多くの分布と関連している.他の分布にも,Benfordの法則を通じてBenfordDistributionに関連しているものがある.例えば,ExponentialDistribution,WeibullDistribution,GammaDistribution,LogLogisticDistribution,ExponentialPowerDistributionに従う確率変数の経験的検定は,Benfordの法則に忠実にしたがっているのに対し,UniformDistribution,HalfNormalDistribution,NormalDistribution,GumbelDistributionによって生成された確率変数はそうではない.他にもいくつかの分布が,その入力母数によって,Benfordの法則と関係する.例えば,ChiSquareDistribution[1]によって生成された確率変数はBenfordの法則に従うが,ChiSquareDistribution[ν]になると,ν が大きくなるにつれて忠実性は低下する.同様に,FRatioDistribution[n,m]の確率変量のサンプルは,n および m の値が小さい場合にBenfordの法則に従うが,n および m が大きくなるにつれて忠実性は低下する.LogNormalDistribution[μ,σ]に従って分布する確率変量は,μ および ν の値が大きい場合はBenfordの法則に従う度合いが大きくなる(ν の摂動の方が μ の摂動よりも影響が大きい.)
例題
すべて開くすべて閉じるスコープ (6)
アプリケーション (3)
Benford分布は複数桁にまたがる値の分布を近似する.裾部が重い分布からサンプルを取る:
ヒストグラムを対応するBenfordDistributionの確率密度関数と比較する:
ヒストグラムを対応するBenfordDistributionの確率密度関数と比較する:
米国の大都市の人口がBenford分布に従うかどうか見てみる:
上位100位までの大都市の人口はBenford分布にあまり従っていない:
Wolfram Research (2010), BenfordDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BenfordDistribution.html.
テキスト
Wolfram Research (2010), BenfordDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BenfordDistribution.html.
CMS
Wolfram Language. 2010. "BenfordDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BenfordDistribution.html.
APA
Wolfram Language. (2010). BenfordDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BenfordDistribution.html