BeniniDistribution
BeniniDistribution[α,β,σ]
形状母数が α と β,尺度母数が σ のBenini分布を表す.
詳細
- BeniniDistributionは対数Rayleigh分布としても知られている.
- Benini分布における値
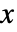 の確率密度は
の確率密度は 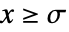 について
について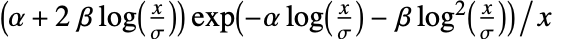 に比例する.
に比例する. - BeniniDistributionでは,α,β,σ は任意の正の実数でよい.
- BeniniDistributionでは,σ は任意の単位次元の数量でよく,α と β は無次元量でよい. »
- BeniniDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- BeniniDistribution[α,β,σ] は,区間
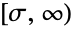 上で定義され,確率密度関数(PDF)の全体的な動作を決定する「形状母数」として知られる2つの正の値 αおよび β でパラメータ化される連続統計分布を表す.σ は,Benini分布のPDFの水平位置を決めるために「局所母数」と呼ばれる正の値である.σ は,値が大きくなるとPDFの全体的な高さが低くなることから,「スケーリング母数」と呼ばれることもある.Benini分布のPDFは,α および β の値によって,単調減少か領域の最左境界に特異値が近付く可能性がある単峰型になる.PDFの裾部は母数 α および β によって,(PDFが
上で定義され,確率密度関数(PDF)の全体的な動作を決定する「形状母数」として知られる2つの正の値 αおよび β でパラメータ化される連続統計分布を表す.σ は,Benini分布のPDFの水平位置を決めるために「局所母数」と呼ばれる正の値である.σ は,値が大きくなるとPDFの全体的な高さが低くなることから,「スケーリング母数」と呼ばれることもある.Benini分布のPDFは,α および β の値によって,単調減少か領域の最左境界に特異値が近付く可能性がある単峰型になる.PDFの裾部は母数 α および β によって,(PDFが 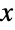 の大きい値について,指数的ではなく代数的に減少するという意味で)「厚い」か,あるいは「薄い」(PDFが
の大きい値について,指数的ではなく代数的に減少するという意味で)「厚い」か,あるいは「薄い」(PDFが 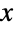 の大きい値について指数的に減少する).(この動作は関数のSurvivalFunctionを解析することで,数量的に正確にできる.)
の大きい値について指数的に減少する).(この動作は関数のSurvivalFunctionを解析することで,数量的に正確にできる.) - Benini分布は,式
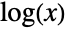 中の二次多項式が,ParetoDistributionの構築に,Vilfredo Paretoが使った一次多項式よりも,モデルへのよりよいフィットを与えることが多いことに気づいたイタリアの統計学者Rodolfo Beniniによって考案された.その考案以来,Benini分布は,保険数理における故障率の考察や経済学における収入分布含む数多くの現象を測定できる潜在能力によって,数多くの分野で基本ツールになっている.
中の二次多項式が,ParetoDistributionの構築に,Vilfredo Paretoが使った一次多項式よりも,モデルへのよりよいフィットを与えることが多いことに気づいたイタリアの統計学者Rodolfo Beniniによって考案された.その考案以来,Benini分布は,保険数理における故障率の考察や経済学における収入分布含む数多くの現象を測定できる潜在能力によって,数多くの分野で基本ツールになっている. - RandomVariateを使ってBenini分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BeniniDistribution[α,β,σ]](より簡略すると xBeniniDistribution[α,β,σ])を使って,確率変数 x がBenini分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BeniniDistribution[α,β,σ],x]およびCDF[BeniniDistribution[α,β,σ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がBenini分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからBeniniパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをBenini分布にフィットすることができる.ProbabilityPlotを使って記号Benini分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Benini分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたBenini分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってBenini分布を含む高次元分布を構築することが,ProductDistributionを使ってBenini分布を含む独立成分分布の結合分布を計算することができる.
- Benini分布は他の数多くの分布と関連している.先に記したように,BeniniDistributionはParetoDistributionの自然な一般化であり,PDF[BeniniDistribution[α,0,σ],x]は,厳密に,PDF[ParetoDistribution[α,σ],x]に等しい.BeniniDistributionは,確率変量
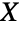 が XRayleighDistribution[σ]を満足するのであるならExp[X]BeniniDistribution[0,1/(2σ2),1]である,という意味においてRayleighDistributionの変換でもある.BeniniDistributionは,WeibullDistributionに従って分布した変量の対数のCDFがBenini分布に従う変量のCDFと等しいという意味で,対数ワイブル分布として言及されることがある.そして,この関係のために,BeniniDistributionはGammaDistribution,ExponentialDistribution,MaxStableDistribution,MinStableDistribution,GumbelDistribution,FrechetDistribution,UniformDistributionとも密接な関係がある.
が XRayleighDistribution[σ]を満足するのであるならExp[X]BeniniDistribution[0,1/(2σ2),1]である,という意味においてRayleighDistributionの変換でもある.BeniniDistributionは,WeibullDistributionに従って分布した変量の対数のCDFがBenini分布に従う変量のCDFと等しいという意味で,対数ワイブル分布として言及されることがある.そして,この関係のために,BeniniDistributionはGammaDistribution,ExponentialDistribution,MaxStableDistribution,MinStableDistribution,GumbelDistribution,FrechetDistribution,UniformDistributionとも密接な関係がある.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
BeniniDistributionを使って猫の体重をモデル化することができる:
BeniniDistributionは損失のモデル化に使うことができる:
明らかな外れ値である最も被害の大きかったハリケーンアンドリューを除き,通貨単位を加える:
これから来る強力な30のハリケーンの予想される損失のシミュレーションを単位を百万USドルとして行う:
BenktanderGibratDistributionと関連する定常更新分布を求める:
BeniniDistributionと比較する:
特性と関係 (5)
Benini分布は正の因子によるスケーリングの下では閉じている:
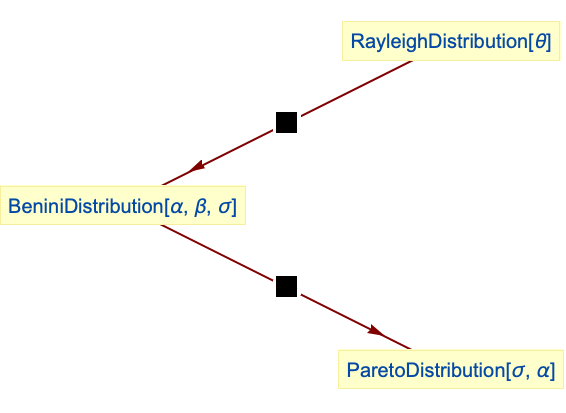
ParetoDistributionはBeniniDistributionの特殊ケースである:
Benini分布はRayleighDistributionを変換したものである:
テキスト
Wolfram Research (2010), BeniniDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BeniniDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "BeniniDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BeniniDistribution.html.
APA
Wolfram Language. (2010). BeniniDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BeniniDistribution.html