BenktanderGibratDistribution[a,b]
represents a Benktander distribution of type I with parameters a and b.


BenktanderGibratDistribution
BenktanderGibratDistribution[a,b]
represents a Benktander distribution of type I with parameters a and b.
Details
- The probability density for value
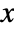 in a Benktander–Gibrat distribution is proportional to
in a Benktander–Gibrat distribution is proportional to 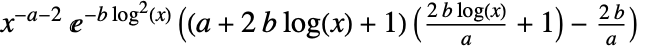 for
for 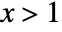 .
. - BenktanderGibratDistribution allows
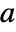 and
and 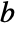 to be any positive real numbers such that
to be any positive real numbers such that 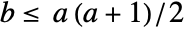 .
. - BenktanderGibratDistribution allows a and b to be dimensionless quantities. »
- BenktanderGibratDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BenktanderGibratDistribution[a,b] represents a continuous statistical distribution defined over the interval
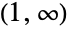 and parametrized by two positive values a, b that satisfy
and parametrized by two positive values a, b that satisfy 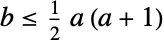 and that determine the overall behavior of the probability density function (PDF). Depending on the values of a and b, the PDF of the Benktander–Gibrat distribution may be monotonic decreasing or may be unimodal, with potential singularities approaching the leftmost boundary of its domain. The tails of the PDF of BenktanderGibratDistribution are "heavy" (in the sense that the PDF decreases more slowly than exponentially for large values
and that determine the overall behavior of the probability density function (PDF). Depending on the values of a and b, the PDF of the Benktander–Gibrat distribution may be monotonic decreasing or may be unimodal, with potential singularities approaching the leftmost boundary of its domain. The tails of the PDF of BenktanderGibratDistribution are "heavy" (in the sense that the PDF decreases more slowly than exponentially for large values 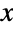 ), though the distribution is considered "subexponential" rather than "fat-tailed". (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
), though the distribution is considered "subexponential" rather than "fat-tailed". (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Benktander–Gibrat distributions were formulated by Swedish actuary Gunnar Benktander, who noted that empirical mean excess functions suggest the need for distributions that are "intermediate" between the Pareto and exponential distributions. Most commonly, Benktander–Gibrat distributions are used to model asset loss within actuarial science applications. Moreover, subexponential distributions such as the Benktander–Gibrat are also useful in studying the properties of random walks. Benktander–Gibrat distributions are sometimes called type I Benktander distributions, with the second type of distribution often known as the Benktander–Weibull distribution and implemented as BenktanderWeibullDistribution in the Wolfram Language. Both are considered to be "close to" log-normal distributions, in the sense that the PDFs of the two distributions are qualitatively similar.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Benktander–Gibrat distribution. Distributed[x,BenktanderGibratDistribution[a,b]], written more concisely as xBenktanderGibratDistribution[a,b], can be used to assert that a random variable x is distributed according to a Benktander–Gibrat distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BenktanderGibratDistribution[a,b],x] and CDF[BenktanderGibratDistribution[a,b],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Benktander–Gibrat distribution, EstimatedDistribution to estimate a Benktander–Gibrat parametric distribution from given data, and FindDistributionParameters to fit data to a Benktander–Gibrat distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Benktander–Gibrat distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Benktander–Gibrat distribution.
- TransformedDistribution can be used to represent a transformed Benktander–Gibrat distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Benktander–Gibrat distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Benktander–Gibrat distributions.
- BenktanderGibratDistribution is related to a number of other statistical distributions. For example, as previously noted, both BenktanderGibratDistribution and BenktanderWeibullDistribution belong to the same "family" of distributions, namely those that are considered intermediate between ParetoDistribution and ExponentialDistribution. Qualitatively, the PDF of BenktanderGibratDistribution is similar to that of LogNormalDistribution, thus inducing (qualitative) relationships between BenktanderGibratDistribution and both NormalDistribution and JohnsonDistribution. ParetoDistribution is considered a limiting case of BenktanderGibratDistribution, in the sense that the PDF of BenktanderGibratDistribution[a,b] tends to that of ParetoDistribution[1,a+1] whenever b tends to 0. This fact implies that the PDFs of both BenktanderGibratDistribution[a,b] and BenktanderWeibullDistribution[a,b] approach the same limiting function as b tends to 0. Furthermore, the stationary renewal distribution associated with a Benktander–Gibrat distribution has precisely the same formula on its domain as the PDF of BeniniDistribution[a,b,1].
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Benktander–Gibrat distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Use dimensionless Quantity to define BenktanderGibratDistribution:
Applications (3)
An insurance company finds its claim sizes in units of deductibles follow a Benktander type I distribution with parameters ![]() and
and ![]() . Find the probability that claim sizes will exceed 2:
. Find the probability that claim sizes will exceed 2:
Compute the mean excess function for a Benktander type I distribution:
For large ![]() , it approaches that of log-normal, also known as Gibrat distribution:
, it approaches that of log-normal, also known as Gibrat distribution:
Now replace the complimentary error function with its asymptotics at large arguments:
Find stationary renewal distribution associated with a Benktander type I distribution:
Compare it with BeniniDistribution:
Properties & Relations (3)
Relationships to other distributions:
A ParetoDistribution is the limiting case of BenktanderGibratDistribution:
Related Guides
Text
Wolfram Research (2010), BenktanderGibratDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BenktanderGibratDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BenktanderGibratDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BenktanderGibratDistribution.html.
APA
Wolfram Language. (2010). BenktanderGibratDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BenktanderGibratDistribution.html
BibTeX
@misc{reference.wolfram_2025_benktandergibratdistribution, author="Wolfram Research", title="{BenktanderGibratDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BenktanderGibratDistribution.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_benktandergibratdistribution, organization={Wolfram Research}, title={BenktanderGibratDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BenktanderGibratDistribution.html}, note=[Accessed: 24-February-2026]}