BeniniDistribution
BeniniDistribution[α,β,σ]
表示形状参数为 α 和 β、尺度参数为 σ 的 Benini 分布.
更多信息
- BeniniDistribution 也称为对数-瑞利分布.
- 在 Benini 分布中,当
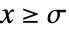 时,值
时,值 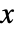 的概率密度与
的概率密度与 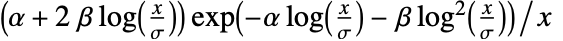 成正比.
成正比. - BeniniDistribution 允许 α、β 和 σ 为任意正实数.
- BeniniDistribution 允许 σ 为任意单位维度的量,α 和 β 为无量纲单位. »
- BeniniDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.
背景
- BeniniDistribution[α,β,σ] 表示一个定义在区间
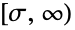 上的连续统计分布,即 Benini 分布,它有两个正的“形状参数” α、β 用于确定其概率密度函数(PDF)的整体行为. 正数 α 被称为“位置参数”因为它决定了 Benini 分布的 PDF 的位置,而 β 也被称为“比例参数”因为 β 越高对应的 PDF 整体高度越小. 根据 α 和 β 的值,Benini 分布的 PDF 可能是单调递减的,也可能是在定义域最左侧逼近潜在奇点的单峰形状. PDF 的尾部可能是“胖的”(意思是说 PDF 在
上的连续统计分布,即 Benini 分布,它有两个正的“形状参数” α、β 用于确定其概率密度函数(PDF)的整体行为. 正数 α 被称为“位置参数”因为它决定了 Benini 分布的 PDF 的位置,而 β 也被称为“比例参数”因为 β 越高对应的 PDF 整体高度越小. 根据 α 和 β 的值,Benini 分布的 PDF 可能是单调递减的,也可能是在定义域最左侧逼近潜在奇点的单峰形状. PDF 的尾部可能是“胖的”(意思是说 PDF 在 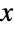 值较大时衰减不是指数的而是代数的)或者“瘦的”(PDF 在
值较大时衰减不是指数的而是代数的)或者“瘦的”(PDF 在 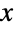 值较大时呈指数衰减),这也取决于参数 α 和 β.(这一行为可通过研究分布的 SurvivalFunction 做精确的定量分析.)
值较大时呈指数衰减),这也取决于参数 α 和 β.(这一行为可通过研究分布的 SurvivalFunction 做精确的定量分析.) - Benini 分布是由意大利统计学家 Rodolfo Benini 提出的,在构造 ParetoDistribution 时他注意到在表达式
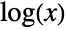 中使用二次多项式比 Vilfredo Pareto 使用的一次多项式能更好的符合模型. 自提出以来,Benini 分布已经成为一些领域的基础工具,因为它具备估测大量现象的潜质,包括精算学中的故障率考虑和经济学中的收入分布.
中使用二次多项式比 Vilfredo Pareto 使用的一次多项式能更好的符合模型. 自提出以来,Benini 分布已经成为一些领域的基础工具,因为它具备估测大量现象的潜质,包括精算学中的故障率考虑和经济学中的收入分布. - RandomVariate 可被用于给出 Benini 分布的一个或多个机器精度或任意精度(后者可用 WorkingPrecision 选项指定)的伪随机变量. Distributed[x,BeniniDistribution[α,β,σ]],更简洁的写法是 xBeniniDistribution[α,β,σ],可被用于声明随机变量 x 是 Benini 分布的. 这样一个声明之后可用在如 Probability、NProbability、Expectation 以及 NExpectation 这样的函数中.
- 概率密度函数和累积分布函数可用 PDF[BeniniDistribution[α,β,σ],x] 和 CDF[BeniniDistribution[α,β,σ],x] 求得. 平均数、中位数、方差、原点矩及中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 计算.
- DistributionFitTest 可被用于测试给定的数据集是否与 Benini 分布一致,EstimatedDistribution 可被用于根据给定数据估算 Benini 参数化分布,而 FindDistributionParameters 可拟合数据和 Benini 分布. ProbabilityPlot 可被用于生成给定数据的 CDF 相对于符号 Benini 分布的 CDF 的图线,而 QuantilePlot 可被用于生成给定数据的分位数相对于符号 Benini 分布的分位数的图线.
- TransformedDistribution 可被用于表示转换的 Benini 分布,CensoredDistribution 可被用于表示删截后位于上限值和下限值之间的值分布,而 TruncatedDistribution 可被用于表示截断后位于上限值和下限值之间的值分布. CopulaDistribution 可被用于建立包含了 Benini 分布的高维分布,而 ProductDistribution 可被用于计算包括 Benini 分布在内的,若干个独立分量分布的联合分布.
- Benini 分布与许多其它分布密切相关. 如前面所指出,BeniniDistribution 是 ParetoDistribution 的自然推广,而且实际上,PDF[BeniniDistribution[α,0,σ],x] 精确等于 PDF[ParetoDistribution[α,σ],x]. BeniniDistribution 也可以从 RayleighDistribution 经过变换得到,这是说如果随机变量 X 满足 XRayleighDistribution[σ],则有 Exp[X]BeniniDistribution[0,1/(2σ2),1]. BeniniDistribution 有时也被称为 log-Weibull 分布,这是因为分布为 WeibullDistribution 的随机变量的 CDF 精确等于 Benini 分布的随机变量的 CDF,而且因为这一关系,BeniniDistribution 也和 GammaDistribution、ExponentialDistribution、MaxStableDistribution、MinStableDistribution、GumbelDistribution、FrechetDistribution 以及 UniformDistribution 密切相关.
范例
打开所有单元关闭所有单元范围 (8)
Quantity 在参数中的一致性使用生成 QuantityDistribution:
应用 (3)
BeniniDistribution 可以用来对猫的体重进行建模:
BeniniDistribution 可用于对损失额建模:
删除明显的异常值,即破坏力最大的飓风 Andrew,并添加货币单位:
求与 BenktanderGibratDistribution 相关的平稳更新分布:
与 BeniniDistribution 比较:
属性和关系 (5)
当使用一个正因子为比例进行缩放时,新生成的分布仍然是 Benini 分布:
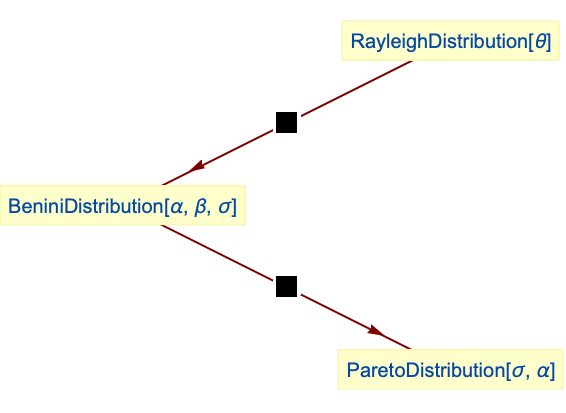
ParetoDistribution 是一种特殊的 BeniniDistribution:
Benini 分布是 RayleighDistribution 的一个变换:
文本
Wolfram Research (2010),BeniniDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BeniniDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "BeniniDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/BeniniDistribution.html.
APA
Wolfram 语言. (2010). BeniniDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BeniniDistribution.html 年