BenktanderWeibullDistribution
BenktanderWeibullDistribution[a,b]
母数が a と b のタイプIIのベンクタンダー(Benktander)分布を表す.
詳細
- ベンクタンダー・ワイブル分布における値
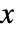 の確率密度は
の確率密度は 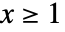 のとき
のとき 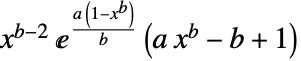 に比例する.
に比例する. - BenktanderWeibullDistributionでは,a は任意の正の実数でよく,
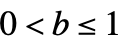 でよい.
でよい. - BenktanderWeibullDistributionでは,a と b は無次元量でよい. »
- BenktanderWeibullDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- BenktanderWeibullDistribution[a,b]は,区間
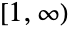 で定義され,正の値 a および b (
で定義され,正の値 a および b (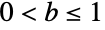 )でパラメータ化される,連続統計分布を表す.パラメータ a および b は,ベンクタンダー・ワイブル分布の確率密度関数(PDF)の全体的な形を決定する.ただし,PDFは単調減少であり,そのようなすべてのパラメータについて区間の最左境界に近付く特異点を持つ可能性がある.BenktanderWeibullDistributionのPDFの裾部は(
)でパラメータ化される,連続統計分布を表す.パラメータ a および b は,ベンクタンダー・ワイブル分布の確率密度関数(PDF)の全体的な形を決定する.ただし,PDFは単調減少であり,そのようなすべてのパラメータについて区間の最左境界に近付く特異点を持つ可能性がある.BenktanderWeibullDistributionのPDFの裾部は(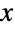 の大きい値については,PDFが指数的よりも遅く減少するという意味で)「重い」.しかし,この分布は「裾部が重い」というよりも「準指数的」であるとみなされている.(この動作は,分布のSurvivalFunctionを解析することで数量的に正確にすることができる.)
の大きい値については,PDFが指数的よりも遅く減少するという意味で)「重い」.しかし,この分布は「裾部が重い」というよりも「準指数的」であるとみなされている.(この動作は,分布のSurvivalFunctionを解析することで数量的に正確にすることができる.) - ベンクタンダー・ワイブル分布は,経験的平均超過関数がパレート分布と指数分布の「中間的」分布の必要性を示唆していることに気付いた,スウェーデンの保険数理士であるGunnar Benktanderによって考案された.ベンクタンダー・ワイブル分布は,保険数理のアプリケーションにおける資産の損失のモデル化に最もよく使われている.さらに,ベンクタンダー・ワイブル分布のような半指数分布は,ランダムウォークの特性を研究する上でも有益である.ベンクタンダー・ワイブル分布は,タイプIIのベンクタンダー分布と呼ばれることがある.タイプIはベンクタンダー・ジブラ分布として知られ,Wolfram言語ではBenktanderGibratDistributionとして実装されている.どちらの分布も,両分布のPDFが数量的に似ている点でワイブル分布に「近い」とみなされている.
- RandomVariateを使ってベンクタンダー・ワイブル分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BenktanderWeibullDistribution[a,b]](より簡略すると xBenktanderWeibullDistribution[a,b])を使って,確率変数 x がベンクタンダー・ワイブル分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BenktanderWeibullDistribution[a,b],x]およびCDF[BenktanderWeibullDistribution[a,b],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がベンクタンダー・ワイブル分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからベンクタンダー・ワイブルパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをベンクタンダー・ワイブル分布にフィットすることができる.ProbabilityPlotを使って記号ベンクタンダー・ワイブル分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ベンクタンダー・ワイブル分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベンクタンダー・ワイブル分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってベンクタンダー・ワイブル分布を含む高次元分布を構築することが,ProductDistributionを使ってベンクタンダー・ワイブル分布を含む独立成分分布の結合分布を計算することができる.
- BenktanderWeibullDistributionは,数多くの他の統計分布と関連している.例えば,先に記したように,BenktanderWeibullDistributionとBenktanderGibratDistributionは,ParetoDistributionとExponentialDistributionの中間分布であるとみなされる同じ分布「族」に属する.定性的には,BenktanderWeibullDistributionのPDFはWeibullDistributionのそれに類似しており,これによってBenktanderWeibullDistributionとGammaDistribution,RayleighDistribution,MaxStableDistribution,MinStableDistribution,ExtremeValueDistribution,GumbelDistribution,FrechetDistributionを含む数多くの分布との(定性)関係が導かれる.BenktanderWeibullDistribution[a,1]は,ExponentialDistribution[a]の切断バージョン( x についての前者のPDFがPDF[TruncatedDistribution[{1,Infinity},ExponentialDistribution[a]],x]と厳密に等しいという意味において)である.同様に,BenktanderWeibullDistributionはシフトされたExponentialDistributionと見ることができる.ParetoDistributionは,b が0に近付くにつれてBenktanderWeibullDistribution[a,b]のPDFがParetoDistribution[1,a+1]のそれに近付くという意味で,BenktanderWeibullDistributionの極限のケースであるとみなされる.この事実は,b が0に近付くにつれてBenktanderWeibullDistribution[a,b]とBenktanderGibratDistribution[a,b]の両方のPDFが同じ極限関数に近付くことを暗に示している.さらに,ベンクタンダー・ワイブル分布に関連する定常再生分布の生存分布は,切断ワイブル分布TruncatedDistribution[{1,∞},WeibullDistribution[b,(b/a)1/b]],x]の生存関数とその領域上で全く同じ式を持つ.
例題
すべて開くすべて閉じるスコープ (8)
ベンクタンダー・ワイブル分布から擬似乱数のサンプルを生成する:
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元のQuantityを使ってBenktanderWeibullDistributionを定義する:
アプリケーション (2)
タイプIIのベンクタンダー分布について平均超過関数を計算する:
大きい ![]() の値に対しては,平均超過関数はワイブル分布のものに近付く:
の値に対しては,平均超過関数はワイブル分布のものに近付く:
タイプIIのベンクタンダー分布に関連する定常再生分布を求める:
切断WeibullDistributionと比較する:
特性と関係 (5)
![]() ではBenktanderWeibullDistributionは準指数的である:
ではBenktanderWeibullDistributionは準指数的である:
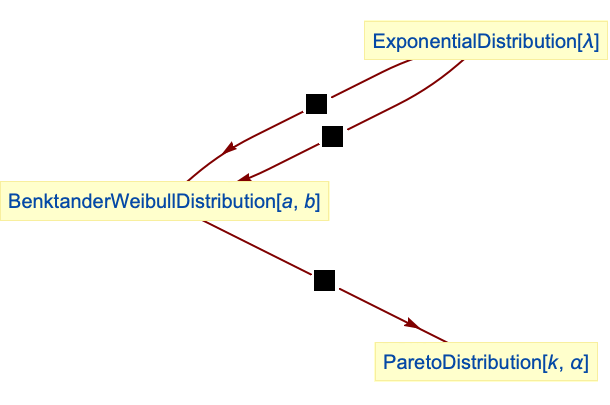
![]() のとき,タイプIiのベンクタンダー分布は切断ExponentialDistributionに簡約される:
のとき,タイプIiのベンクタンダー分布は切断ExponentialDistributionに簡約される:
シフトされたExponentialDistributionはタイプIIのベンクタンダー分布である:
ParetoDistributionはタイプIIのベンクタンダー分布の極限のケースである:
テキスト
Wolfram Research (2010), BenktanderWeibullDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "BenktanderWeibullDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html.
APA
Wolfram Language. (2010). BenktanderWeibullDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html