CircularSymplecticMatrixDistribution
CircularSymplecticMatrixDistribution[n]
表示复数域上的圆辛矩阵分布,其矩阵维数为 {2 n,2 n}.
更多信息
- CircularSymplecticMatrixDistribution 亦称为圆辛系综,或 CSE.
- CircularSymplecticMatrixDistribution 表示自对偶 n 维酉四元数方阵上的均匀分布.
- 矩阵维度参数 n 可以是任意正整数.
- CircularSymplecticMatrixDistribution 可以和诸如 MatrixPropertyDistribution、RandomVariate 之类的函数一起使用.
背景
- CircularSymplecticMatrixDistribution[n],也被称作圆辛系综(CSE),表示在
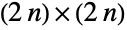 一元自双复数矩阵上的统计分布,即同时满足
一元自双复数矩阵上的统计分布,即同时满足 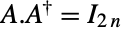 和
和 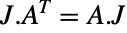 的偶数维复方阵
的偶数维复方阵 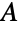 ,其中
,其中 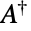 表示
表示 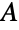 的共轭转置,
的共轭转置,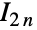 是
是 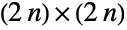 恒等矩阵,
恒等矩阵,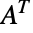 是
是 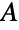 的转置,
的转置,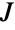 是形如
是形如 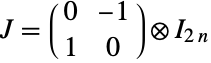 的辛矩阵,其中 ⊗ 是 Kronecker 积. 参数 n 被称作分布的维度参数,可以是任意正整数. 尽管名为“圆辛矩阵分布”,属于该分布的矩阵不一定为辛阵.
的辛矩阵,其中 ⊗ 是 Kronecker 积. 参数 n 被称作分布的维度参数,可以是任意正整数. 尽管名为“圆辛矩阵分布”,属于该分布的矩阵不一定为辛阵. - 与圆正交和圆酉矩阵分布(分别为 CircularOrthogonalMatrixDistribution 和CircularUnitaryMatrixDistribution)一道,圆辛矩阵分布是由 Freeman Dyson 于 1962 年最初设计的三个圆矩阵系综之一,是研究量子力学的工具. 从概率学角度而言,圆辛矩阵分布表示自双酉四元方阵上的均匀分布. 类如圆辛矩阵分布的矩阵系综,在随机矩阵理论以及在物理和数学的各个分支的研究中都具有相当的重要性.
- RandomVariate 可用来给出一个或更多机器精度或任意精度(后者可通过 WorkingPrecision 选项获得)的圆辛矩阵分布中的伪随机变元,并且这类变元的均值、中位数、方差、原始矩和中心矩可以分别通过使用 Mean、Median、Variance、Moment 和 CentralMoment 计算得到. Distributed[A,CircularSymplecticMatrixDistribution[n]],更简洁的式子为 ACircularSymplecticMatrixDistribution[n] ,可用于断定随机矩阵 A 服从圆辛矩阵分布. 这类断言可用于诸如 MatrixPropertyDistribution 的函数中.
- 服从圆辛矩阵分布的变元的迹、特征值和范数可以分别使用 Tr、Eigenvalues 和 Norm 计算得到. 这类变元也可以通过 MatrixFunction、MatrixPower 及相关实量研究,例如实部(Re)、虚部(Im)和复参数(Arg),可以使用 MatrixPlot 绘图.
- CircularSymplecticMatrixDistribution 和许多其它分布有关. 如上所述,它在性质上与其它圆矩阵分布相似,如 CircularQuaternionMatrixDistribution、CircularRealMatrixDistribution、CircularOrthogonalMatrixDistribution 和 CircularUnitaryMatrixDistribution 等. 最初,圆矩阵系综是由所谓广义高斯系综推导而来,因此 CircularSymplecticMatrixDistribution 与GaussianOrthogonalMatrixDistribution、GaussianSymplecticMatrixDistribution 和 GaussianUnitaryMatrixDistribution 相关. CircularSymplecticMatrixDistribution 也与 MatrixNormalDistribution、MatrixTDistribution、WishartMatrixDistribution、 InverseWishartMatrixDistribution、TracyWidomDistribution 和 WignerSemicircleDistribution 相关.
范例
打开所有单元关闭所有单元基本范例 (2)
应用 (1)
CircularSymplecticMatrixDistribution 的特征值的联合分布也是当逆温度 ![]() 时,戴森的库仑气体在圆上的 Boltzmann 分布. 系统中每个粒子的平均哈密顿量(不包含动能项)为:
时,戴森的库仑气体在圆上的 Boltzmann 分布. 系统中每个粒子的平均哈密顿量(不包含动能项)为:
属性和关系 (2)
比较样本水平间距的直方图与解析形式,亦称为 Dyson 指标为4的 Wigner 估测:
对于维度大小为 ![]() 的 CircularSymplecticMatrixDistribution 的特征向量,四元数元素的缩放模数服从
的 CircularSymplecticMatrixDistribution 的特征向量,四元数元素的缩放模数服从 ![]() 分布:
分布:
将直方图与 ChiSquareDistribution 的 PDF 进行比较:
可能存在的问题 (1)
从 CircularSymplecticMatrixDistribution 得来的矩阵不必是辛矩阵:
用 CircularQuaternionMatrixDistribution 随机生成一个酉辛阵:
文本
Wolfram Research (2015),CircularSymplecticMatrixDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CircularSymplecticMatrixDistribution.html.
CMS
Wolfram 语言. 2015. "CircularSymplecticMatrixDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CircularSymplecticMatrixDistribution.html.
APA
Wolfram 语言. (2015). CircularSymplecticMatrixDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CircularSymplecticMatrixDistribution.html 年