WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

ConicHullRegion[{p1,…,pm+1}]

点 piを通る m 次元アフィン包領域を表す．

ConicHullRegion[p,{v1,…,vm}]

点 p を通り viと平行な m 次元アフィン包領域を表す．

ConicHullRegion[{p1,…,pm+1},{w1,…,wn}]

m 次元アフィン包にベクトル wjで生成された錐包を加えた領域を表す．

ConicHullRegion[p,{v1,…,vm},{w1,…,wn}]

m 次元アフィン包にベクトル wjで生成された錐包を加えた領域を表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
グラフィックス  
指定  
スタイリング  
座標  
領域  
アプリケーション  
特性と関係  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

ConicHullRegion

ConicHullRegion[{p1,…,pm+1}]

点 piを通る m 次元アフィン包領域を表す．

ConicHullRegion[p,{v1,…,vm}]

点 p を通り viと平行な m 次元アフィン包領域を表す．

ConicHullRegion[{p1,…,pm+1},{w1,…,wn}]

m 次元アフィン包にベクトル wjで生成された錐包を加えた領域を表す．

ConicHullRegion[p,{v1,…,vm},{w1,…,wn}]

m 次元アフィン包にベクトル wjで生成された錐包を加えた領域を表す．

詳細

  • ConicHullRegionは，アフィン空間，半空間，特殊ケースのアフィン包としても知られている．
  • ConicHullRegionは，幾何学領域およびグラフィックスプリミティブとして使うことができる．
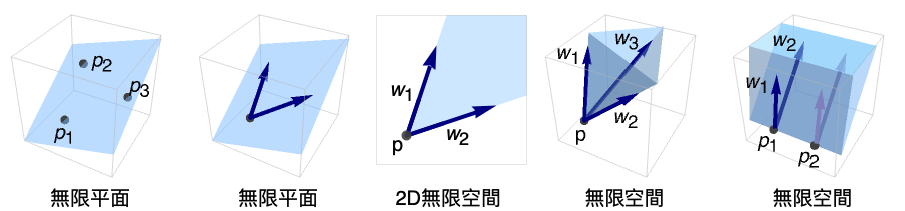
  • ConicHullRegion[{p1,…,pm+1}]およびConicHullRegion[p,{v1,…,vm}]は，アフィン包を表す．これは，一般に，無限線，無限平面，あるいは無限空間として知られているものである．
  • 円錐方向 wjは，アフィン包内の各点に加えられる純粋な錐包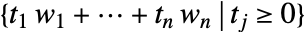を表す．これは，アフィン包および錐包のMinkowski和としても知られている．
  • パラメータ表現は以下で与えられる．
  • ConicHullRegion[{p1,…,pm+1}]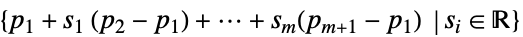
    ConicHullRegion[p,{v1,…,vm}]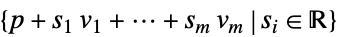
    ConicHullRegion[{p1,…,pm+1},{w1,…,wn}]
    ConicHullRegion[p,{v1,…,vm},{w1,…,wn}]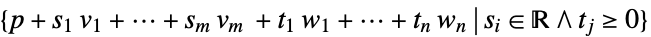
  • ConicHullRegionの低次元バージョンには特別な表し方がある．
  • ConicHullRegion[{p1,p2}]InfiniteLine[{p1,p2}]
    ConicHullRegion[{p1,p2,p3}]InfinitePlane[{p1,p2,p3}]
    ConicHullRegion[{p1},{w1}]HalfLine[p1,w1]
    ConicHullRegion[{p1,p2},{w1}]HalfPlane[{p1,p2},w1]
  • ConicHullRegion[p,{v1,…,vm}]は，viが線形独立の場合は m 次元領域を表す．
  • ConicHullRegionはGraphicsおよびGraphics3Dで使うことができる．
  • グラフィックスでは，点 p，piおよびベクトル vi，wjはDynamic式でよい．
  • グラフィックスの描画は，FaceForm，EdgeForm，Opacity，色等の指示子の影響を受ける．

例題

すべて開く すべて閉じる

例  (3)

2DにおけるConicHullRegion：

Wolfram Language code: Graphics[ConicHullRegion[{{0, 0}}, {{1, -1}, {1, 1}}]]

3Dにおける：

Wolfram Language code: Graphics3D[ConicHullRegion[{{0, 0, 0}}, {{-10, 2, 3}, {1, 1, 0}}]]

さまざまなスタイルが適用された錐包領域：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0}}, {{1, -1}, {1, 1}}];
Wolfram Language code: {Graphics[{Pink, ℛ}], Graphics[{EdgeForm[Thick], Pink, ℛ}], Graphics[{EdgeForm[Dashed], Pink, ℛ}], Graphics[{EdgeForm[Directive[Thick, Dashed, Blue]], Pink, ℛ}]}

指定された錐包領域に点が属するかどうかを見る：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0}}, {{1, -1}, {1, 1}}];
Wolfram Language code: {RegionMember[ℛ, {1, 0}], RegionMember[ℛ, {-1, 0}]}

スコープ  (25)

グラフィックス  (15)

指定  (7)

{1,1}と{3,2}を通る無限線を定義する：

Wolfram Language code: ill = Graphics[{PointSize[Medium], Point[{{1, 1}, {3, 2}}]}, PlotRange -> {{0, 4}, {0, 3}}, Frame -> True];
Wolfram Language code: Show[ill, Graphics[ConicHullRegion[{{1, 1}, {3, 2}}]]]

{1,1}を通って{2,1}の方向に進む同じ線を定義する：

Wolfram Language code: ill = Graphics[{PointSize[Medium], Point[{{1, 1}}], Arrowheads[Medium], Thick, Arrow[{{1, 1}, {3, 2}}]}, PlotRange -> {{0, 4}, {0, 3}}, Frame -> True];
Wolfram Language code: Show[ill, Graphics[ConicHullRegion[{1, 1}, {{2, 1}}]]]

点，ベクトル，円錐方向を使って，上半平面を定義する：

Wolfram Language code: ill = Graphics[{PointSize[Medium], Point[{{0, 0}}], Arrowheads[Medium], Thick, Arrow[{{0, 0}, {1, 0}}], Arrow[{{0, 0}, {0, 1}}]}];
Wolfram Language code: Show[Graphics[{Pink, ConicHullRegion[{0, 0}, {{1, 0}}, {{0, 1}}]}, PlotRange -> {{-1, 2}, {-1, 2}}, Frame -> True], ill]

点と2つの円錐方向を使って2Dの無限空間を定義する：

Wolfram Language code: ill = Graphics[{PointSize[Medium], Point[{{0, 0}}], Arrowheads[Medium], Thick, Arrow[{{0, 0}, {1, 1}}], Arrow[{{0, 0}, {-1, 1}}]}];
Wolfram Language code: Show[Graphics[{Pink, ConicHullRegion[{{0, 0}}, {{1, 1}, {-1, 1}}]}, PlotRange -> {{-2, 2}, {-1, 2}}, Frame -> True], ill]

との両点を通る3Dにおける無限線を定義する：

Wolfram Language code: ill = Graphics3D[{PointSize[Medium], Point[{{1, 1, 1}, {2, 3, 4}}]}, PlotRange -> 5, Axes -> True];
Wolfram Language code: Show[ill, Graphics3D[ConicHullRegion[{{1, 1, 1}, {2, 3, 4}}]]]

点と方向ベクトルを使って同じ線を定義する：

Wolfram Language code: ill = Graphics3D[{PointSize[Medium], Point[{{1, 1, 1}}], Arrowheads[Medium], Thick, Arrow[{{1, 1, 1}, {2, 3, 4}}]}, PlotRange -> 5, Axes -> True];
Wolfram Language code: Show[ill, Graphics3D[ConicHullRegion[{1, 1, 1}, {{1, 2, 3}}]]]

点，，を通る平面を定義する：

Wolfram Language code: ill = Graphics3D[{PointSize[Medium], Point[{{0, 1, 3}, {1, 0, 1}, {1, 2, 3}}]}, PlotRange -> {{-1, 2}, {-1, 3}, {0, 4}}, Axes -> True];
Wolfram Language code: Show[ill, Graphics3D[{Opacity[0.5], ConicHullRegion[{{0, 1, 3}, {1, 0, 1}, {1, 2, 3}}]}]]

点と方向ベクトルを使って同じ平面を定義する：

Wolfram Language code: ill = Graphics3D[{PointSize[Medium], Point[{{0, 1, 3}}], Arrowheads[Medium], Thick, Arrow[{{0, 1, 3}, {1, 0, 1}}], Arrow[{{0, 1, 3}, {1, 2, 3}}]}, PlotRange -> {{-1, 2}, {-1, 3}, {0, 4}}, Axes -> True];
Wolfram Language code: Show[ill, Graphics3D[{Opacity[0.5], ConicHullRegion[{0, 1, 3}, {{1, -1, -2}, {1, 1, 0}}]}]]

尖端が，方向がおよびの2Dの無限円錐を定義する：

Wolfram Language code: ill = Graphics3D[{PointSize[Medium], Point[{{0, 0, 0}}], Arrowheads[Medium], Thick, Arrow[{{0, 0, 0}, {0, 1, 2}}], Arrow[{{0, 0, 0}, {1, 2, 0}}]}, PlotRange -> {{-1, 3}, {-1, 3}, {-1, 3}}, Axes -> True];
Wolfram Language code: Show[ill, Graphics3D[ConicHullRegion[{{0, 0, 0}}, {{0, 1, 2}, {1, 2, 0}}]]]

3D半空間は，1つの点，2つのベクトル，円錐方向によって定義できる：

Wolfram Language code: Graphics3D[ConicHullRegion[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}, {{0, 0, 1}}]]

3D無限空間は，1つの点といくつかの円錐方向によって定義できる：

Wolfram Language code: Graphics3D[ConicHullRegion[{{0, 0, 0}}, {{1, 1, 0}, {0, 1, 1}, {1, 0, 1}}]]

スタイリング  (7)

さまざまな太さの1D錐包領域：

Wolfram Language code: Table[Graphics[{Thickness[i], ConicHullRegion[{{0, 0}, {2, 1}}]}], {i, {Tiny, Small, Medium, Large}}]
Wolfram Language code: Table[Graphics[{t, ConicHullRegion[{{0, 0}, {2, 1}}]}], {t, {Thin, Thick}}]

スケールされたサイズによる太さ：

Wolfram Language code: Table[Graphics[{Thickness[i], ConicHullRegion[{{0, 0}, {2, 1}}]}], {i, {.005, .05, .1}}]

印刷用ポイント数による太さ：

Wolfram Language code: Table[Graphics[{AbsoluteThickness[i], ConicHullRegion[{{0, 0}, {2, 1}}]}], {i, {1, 5, 10}}]

破線あるいは点線スタイルを使って1Dの錐包領域を描画することができる：

Wolfram Language code: Table[Graphics[{Dashing[i], ConicHullRegion[{{0, 0}, {2, 1}}]}], {i, {Tiny, Small, Medium, Large}}]
Wolfram Language code: Table[Graphics[{d, ConicHullRegion[{{0, 0}, {2, 1}}]}], {d, {Dotted, Dashed, DotDashed}}]

色指示子を用いて1D錐包領域の辺の色を指定する：

Wolfram Language code: Table[Graphics[{c, ConicHullRegion[{{0, 0}, {2, 1}}]}], {c, {Red, Green, Blue, Yellow}}]

色指示子で，より高次の領域の面の色を指定する：

Wolfram Language code: Table[Graphics[{c, ConicHullRegion[{{0, 0}}, {{1, -1}, {1, 2}}]}], {c, {Red, Green, Blue, Yellow}}]
Wolfram Language code: Table[Graphics3D[{c, ConicHullRegion[{{1, 0, 0}, {1, 1, 1}, {0, 0, 1}}]}], {c, {Red, Green, Blue, Yellow}}]

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定することができる：

Wolfram Language code: Graphics[{FaceForm[Pink], EdgeForm[Directive[Dashed, Thick, Blue]], ConicHullRegion[{{0, 0}}, {{1, -1}, {1, 2}}]}]
Wolfram Language code: Graphics3D[{FaceForm[Pink], EdgeForm[Directive[Dashed, Thick, Blue]], ConicHullRegion[{{1, 0, 0}, {1, 1, 1}, {0, 0, 1}}]}]

3Dでは，FaceFormを使って面の表と裏に異なる特性を指定することができる：

Wolfram Language code: p = {FaceForm[Yellow, Blue], ConicHullRegion[{{0, 0, 0}}, {{1, -1, 0}, {1, 2, 0}}]};
Wolfram Language code: {Graphics3D[p, ViewPoint -> Top], Graphics3D[p, ViewPoint -> Bottom]}

座標  (1)

Scaled座標を2Dで使うことができる：

Wolfram Language code: Graphics[ConicHullRegion[Scaled[{0, 0}], {Scaled[{1, 1}]}], Frame -> True]

3Dでも使うことができる：

Wolfram Language code: Graphics3D[ConicHullRegion[Scaled[{0, 0, 0}], {Scaled[{1, 1, 0}], Scaled[{0, 1, 1}]}]]

領域  (10)

埋込み次元はConicHullRegionがある次元である：

Wolfram Language code: line = ConicHullRegion[{0, 0}, {{1, 1}}]; hplane = ConicHullRegion[{0, 0}, {{1, 1}}, {{1, 0}}];
Wolfram Language code: RegionEmbeddingDimension /@ {line, hplane}

幾何次元は領域それ自体の次元である：

Wolfram Language code: RegionDimension /@ {line, hplane}

点の帰属判定：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0, 0}, {1, 1, 1}}];
Wolfram Language code: {RegionMember[ℛ, {2, 2, 2}], RegionMember[ℛ, {2, 2, 3}]}

点の帰属条件を得る：

Wolfram Language code: RegionMember[ℛ, {x, y, z}]

ConicHullRegionは無限測度を持つ：

Wolfram Language code: ℛ = ConicHullRegion[{{1, 2}, {3, 4}}];
Wolfram Language code: RegionMeasure[ℛ]

重心も不定である：

Wolfram Language code: RegionCentroid[ℛ]

点からの距離：

Wolfram Language code: ℛ = ConicHullRegion[{{2, 2}}, {{3, 1}, {1, 3}}];
Wolfram Language code: RegionDistance[ℛ, {0, 1}]

最近点までの距離：

Wolfram Language code: {Plot3D[Evaluate@RegionDistance[ℛ, {x, y}], {x, 1, 3}, {y, 1, 3}, MeshFunctions -> {#3&}, Mesh -> 5, Exclusions -> None], ContourPlot[Evaluate@RegionDistance[ℛ, {x, y}], {x, 0, 4}, {y, 0, 4}, Contours -> {{0.5, Red}, {1, Green}, {1.5, Blue}}, Exclusions -> None]}

点からの符号付き距離：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0}, {1, 0}}, {{0, 1}}];
Wolfram Language code: SignedRegionDistance[ℛ, {2, 3}]

領域内の最近点：

Wolfram Language code: ℛ = ConicHullRegion[{{2, 2}, {3, 3}}];
Wolfram Language code: RegionNearest[ℛ, {5, 6}]

これを可視化する：

Wolfram Language code: pts = Table[{1, 2} + 5{Cos[k 2 π / 16], Sin[k 2π / 16]}, {k, 0., 15}]; nst = RegionNearest[ℛ, #]& /@ pts;
Wolfram Language code: Legended[Graphics[{{Thick, Gray, ℛ}, {Thin, Gray, Line[Transpose[{pts, nst}]]}, {Red, Point[pts]}, {Blue, Point[nst]}}], PointLegend[{Red, Blue}, {"start", "nearest"}]]

錐包領域は有界ではない：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0, 0}, {1, 0, 0}}, {{0, 1, 0}}];
Wolfram Language code: BoundedRegionQ[ℛ]

しかし，すべての次元で有界ではない訳ではないかもしれない：

Wolfram Language code: RegionBounds[ℛ]

ConicHullRegion上で積分(Integrate)する：

Wolfram Language code: ℛ = ConicHullRegion[{0, 0}, {{1, 0}, {0, 1}}];
Wolfram Language code: Integrate[Exp[-(x^2 + y^2)], {x, y}∈ℛ]

錐包領域上で最適化する：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 1}, {1, 0}}, {{1, 1}}];
Wolfram Language code: Maximize[{-(x^2 + y^2), {x, y}∈ℛ}, {x, y}]

錐包上で方程式を解く：

Wolfram Language code: ℛ = ConicHullRegion[{{0, 0}}, {{0, 1}, {1 / 2, 1 / 2}}];
Wolfram Language code: Reduce[x^2 + y^2 == 1 && {x, y}∈ℛ, {x, y}]

アプリケーション  (4)

各象限を占める領域を定義する：

Wolfram Language code: rl = Flatten[Table[ConicHullRegion[{{0, 0}}, {{x, 0}, {0, y}}], {x, {-1, 1}}, {y, {-1, 1}}]]
Wolfram Language code: Table[Graphics[{StandardBlue, r}, Axes -> True], {r, rl}]

各象限を占める領域を定義する：

Wolfram Language code: rl = Flatten[Table[ConicHullRegion[{{0, 0, 0}}, {{x, 0, 0}, {0, y, 0}, {0, 0, z}}], {x, {-1, 1}}, {y, {-1, 1}}, {z, {-1, 1}}]];
Wolfram Language code: Graphics3D /@ rl

中心点および円上の点から錐包領域を構築する：

Wolfram Language code: rl = Table[ConicHullRegion[{{0, 0, -1}}, Table[{Cos[k 2π / n], Sin[k 2π / n], 1}, {k, 0., n - 1}]], {n, 3, 12, 3}];
Wolfram Language code: Table[Graphics3D[{Opacity[0.5], Yellow, r}, PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}], {r, rl}]

中心点とパラメトリック曲線上の点から錐包領域を構築する：

Wolfram Language code: o = {0, 0, 0}; f[t_] := {16Sin[t] ^ 3, 13Cos[t] - 5Cos[2t] - 2Cos[3t] - Cos[4t], 16}; pts = Table[f[t], {t, 0, 2π, 0.1}];
Wolfram Language code: chr = ConicHullRegion[{o}, pts]; Graphics3D[chr, PlotRange -> {{-16, 16}, {-17, 12}, {0, 16}}]

特性と関係  (5)

InfiniteLineはConicHullRegionの特殊ケースである：

Wolfram Language code: pl = {{1, 2}, {3, 4}};
Wolfram Language code: Reduce[{x, y}∈ConicHullRegion[pl]⧦{x, y}∈InfiniteLine[pl], {x, y}, Reals]

HalfLineはConicHullRegionの特殊ケースである：

Wolfram Language code: Subscript[ℛ, 1] = ConicHullRegion[{{0, 0}}, {{1, 1}}]; Subscript[ℛ, 2] = HalfLine[{0, 0}, {1, 1}];
Wolfram Language code: RegionEqual[Subscript[ℛ, 1], Subscript[ℛ, 2]]

InfinitePlaneはConicHullRegionの特殊ケースである：

Wolfram Language code: Subscript[ℛ, 1] = ConicHullRegion[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}]; Subscript[ℛ, 2] = InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}];
Wolfram Language code: RegionEqual[Subscript[ℛ, 1], Subscript[ℛ, 2]]

HalfPlaneはConicHullRegionの特殊ケースである：

Wolfram Language code: Subscript[ℛ, 1] = ConicHullRegion[{{0, 0}, {1, 0}}, {{0, 1}}]; Subscript[ℛ, 2] = HalfPlane[{{0, 0}, {1, 0}}, {0, 1}];
Wolfram Language code: RegionEqual[Subscript[ℛ, 1], Subscript[ℛ, 2]]

ImplicitRegionは，任意のConicHullRegionを表すことができる：

Wolfram Language code: Subscript[ℛ, 1] = ImplicitRegion[-1 - x + y == 0, {x, y}];
Wolfram Language code: Subscript[ℛ, 2] = ConicHullRegion[{{1, 2}, {3, 4}}];
Wolfram Language code: RegionEqual[Subscript[ℛ, 1], Subscript[ℛ, 2]]

おもしろい例題  (1)

ランダムなアフィン円錐の集合：

Wolfram Language code: Graphics[{EdgeForm[Black], Table[{Hue[RandomReal[]], Opacity[0.1], ConicHullRegion[{RandomReal[1, 2]}, RandomReal[{-1, 1}, {2, 2}]]}, {75}]}]
Wolfram Research (2014), ConicHullRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConicHullRegion.html.

テキスト

Wolfram Research (2014), ConicHullRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConicHullRegion.html.

CMS

Wolfram Language. 2014. "ConicHullRegion." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConicHullRegion.html.

APA

Wolfram Language. (2014). ConicHullRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConicHullRegion.html

BibTeX

@misc{reference.wolfram_2026_conichullregion, author="Wolfram Research", title="{ConicHullRegion}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ConicHullRegion.html}", note=[Accessed: 19-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_conichullregion, organization={Wolfram Research}, title={ConicHullRegion}, year={2014}, url={https://reference.wolfram.com/language/ref/ConicHullRegion.html}, note=[Accessed: 19-June-2026]}