DagumDistribution[p,a,b]
represents a Dagum distribution with shape parameters p and a and scale parameter b.


DagumDistribution
DagumDistribution[p,a,b]
represents a Dagum distribution with shape parameters p and a and scale parameter b.
Details
- DagumDistribution is also known as Burr III distribution.
- The probability density for value
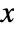 in a Dagum distribution is proportional to
in a Dagum distribution is proportional to 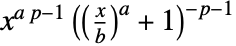 for
for 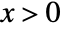 .
. - DagumDistribution allows p, a, and b to be any positive real numbers.
- DagumDistribution allows b to be a quantity of any unit dimension, and p and a to be dimensionless quantities. »
- DagumDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- DagumDistribution[p,a,b] represents a continuous statistical distribution defined over the interval
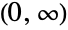 and parametrized by three positive values p, a, and b. The parameters p and a are called "shape parameters" and, depending on their values, the probability density function (PDF) of the Dagum distribution may be monotonic decreasing with potential singularities approaching the lower boundary of its domain or may be unimodal. The parameter b is a "scale parameter" that determines the overall height of the PDF (with the height increasing as the value of b decreases towards zero). Independent of its parameter values, the tails of the PDF of a Dagum distribution are "fat" in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values
and parametrized by three positive values p, a, and b. The parameters p and a are called "shape parameters" and, depending on their values, the probability density function (PDF) of the Dagum distribution may be monotonic decreasing with potential singularities approaching the lower boundary of its domain or may be unimodal. The parameter b is a "scale parameter" that determines the overall height of the PDF (with the height increasing as the value of b decreases towards zero). Independent of its parameter values, the tails of the PDF of a Dagum distribution are "fat" in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values 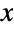 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Dagum distribution is sometimes referred to as a Burr III distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Dagum distribution is sometimes referred to as a Burr III distribution. - The Dagum distribution dates to the work of Argentinian statistician and economist Camilo Dagum in the 1970s. Noting that the income elasticity of the cumulative distribution function (CDF) of income is a decreasing and bounded function, Dagum set out to construct a statistical distribution that closely modeled the distribution of wealth by combining the positive aspects of the Pareto and log-normal distributions (ParetoDistribution and LogNormalDistribution, respectively). Unsurprisingly, the main applications of the Dagum distribution are in economics and actuarial science, though more recently, the distribution has been used to model a number of phenomena in various areas, including tropospheric ozone levels in the field of environmental sciences and lifetime data/survival analysis in statistics.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Dagum distribution. Distributed[x,DagumDistribution[p,a,b]], written more concisely as xDagumDistribution[p,a,b], can be used to assert that a random variable x is distributed according to a Dagum distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[DagumDistribution[p,a,b],x] and CDF[DagumDistribution[p,a,b],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively, though because of the fat tails of the Dagum distribution, some of these quantities may fail to exist.
- DistributionFitTest can be used to test if a given dataset is consistent with a Dagum distribution, EstimatedDistribution to estimate a Dagum parametric distribution from given data, and FindDistributionParameters to fit data to a Dagum distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Dagum distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic beta distribution.
- TransformedDistribution can be used to represent a transformed Dagum distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Dagum distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Dagum distributions.
- The Dagum distribution is related to a number of other distributions. For example, DagumDistribution is a special case of BetaPrimeDistribution in the sense that the PDF of BetaPrimeDistribution[p,1,a,b] is precisely the same as the PDF of DagumDistribution[p,a,b]. DagumDistribution also generalizes the more specific LogLogisticDistribution, i.e. DagumDistribution[1,γ,σ] has the same PDF as LogLogisticDistribution[λ,σ] and is constructed to combine the qualitative features of both LogNormalDistribution and ParetoDistribution. DagumDistribution is the inverse of the Burr/Singh–Maddala distribution (SinghMaddalaDistribution) and is also related to BeniniDistribution, GammaDistribution, and WeibullDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Dagum distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends on the shape parameters a and p and is defined for ![]() :
:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Hazard function is unimodal for ![]() and decreasing otherwise:
and decreasing otherwise:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (4)
DagumDistribution can be used to model incomes:
Adjust part-time to full-time and select nonzero values:
Fit Dagum distribution to the data:
Compare the histogram of the data to the PDF of the estimated distribution:
Find average income at a large state university:
Find the probability that a salary is at most $25,000:
Find the probability that a salary is at least $150,000:
Simulate the incomes for 100 randomly selected employees of such a university:
DagumDistribution can be used to model state per capita incomes:
Fit Dagum distribution to the data:
Compare the histogram of the data to the PDF of the estimated distribution:
Find average income per capita:
Find states with income close to the average:
Find the median income per capita:
Find states with income close to the median:
DagumDistribution can be used to model size; consider the depth (in mm) of leptograpsus crabs:
Fit Dagum distribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the average depth of a crab:
Find the probability that a crab is deeper than 15 mm:
DagumDistribution can be used to model waiting times:
Fit Dagum distribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the average number of days between major earthquakes:
Find the probability that there are at least 200 days between two serious earthquakes:
Properties & Relations (7)
Dagum distribution is closed under scaling by a positive factor:
Dagum distribution is closed under Max:
The Dagum distribution is unimodal for ![]() , and zero modal otherwise:
, and zero modal otherwise:
Relationships to other distributions:
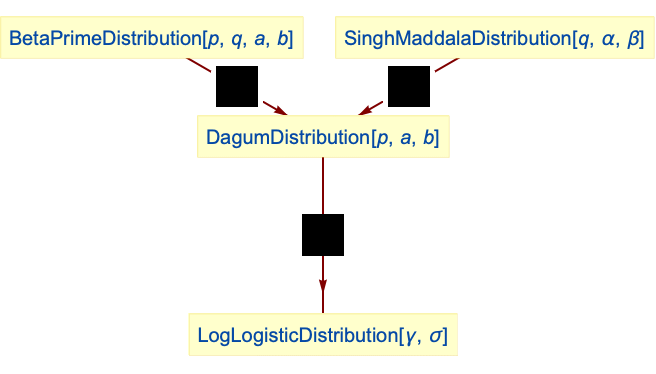
DagumDistribution is a special case of BetaPrimeDistribution:
DagumDistribution is the inverse of SinghMaddalaDistribution:
LogLogisticDistribution is a special case of DagumDistribution:
Related Guides
Text
Wolfram Research (2010), DagumDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/DagumDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "DagumDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/DagumDistribution.html.
APA
Wolfram Language. (2010). DagumDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DagumDistribution.html
BibTeX
@misc{reference.wolfram_2025_dagumdistribution, author="Wolfram Research", title="{DagumDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DagumDistribution.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_dagumdistribution, organization={Wolfram Research}, title={DagumDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/DagumDistribution.html}, note=[Accessed: 24-February-2026]}