DiggleGatesPointProcess
✖
DiggleGatesPointProcess
represents a Diggle–Gates point process with constant intensity μ and interaction radius ρ in 
.
Details
- DiggleGatesPointProcess models point configurations where the points have a softcore decreasing repulsive pairwise interaction for points within radius ρ of each other and that are otherwise uniformly distributed.
-
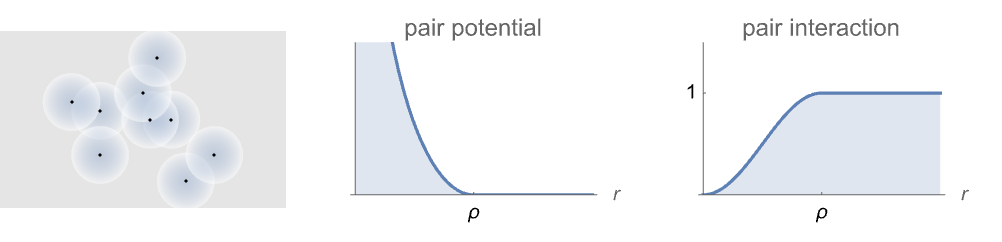
- The Diggle–Gates point process can be defined as a GibbsPointProcess in terms of its intensity μ and the pair potential
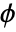or pair interaction 
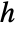, which are both parametrized by ρ as follows: -
pair potential 
pair interaction - A point configuration
from a Diggle–Gates point process DiggleGatesPointProcess[μ,ρ,d] in an observation region reg has density function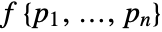 
proportional to ![mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])](Files/DiggleGatesPointProcess.en/9.png "mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])")
, with respect to PoissonPointProcess[1,d]. - The Papangelou conditional density
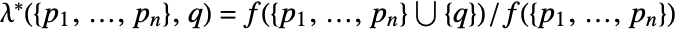for adding a point 
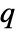to a point configuration 
is ![mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])](Files/DiggleGatesPointProcess.en/13.png "mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])")
. - DiggleGatesPointProcess allows μ and ρ to be any positive number, and d to be any positive integer.
- DiggleGatesPointProcess is a special case of GibbsPointProcess.
- DiggleGatesPointProcess simplifies to PoissonPointProcess when
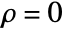. - Possible Method settings in RandomPointConfiguration for StraussPointProcess are:
-
"MCMC" Markov chain Monte Carlo birth and death "Exact" coupling from the past - Possible PointProcessEstimator settings in EstimatedPointProcess for DiggleGatesPointProcess are:
-
Automatic automatically choose the parameter estimator "MaximumPseudoLikelihood" maximize the pseudo-likelihood - DiggleGatesPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.
Examples
open allclose allBasic Examples (2)Summary of the most common use cases
Sample from a Diggle–Gates point process:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-cr2aru
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-tfb0w
Visualize the points in the sample:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-1pasjf
Sample from a Diggle–Gates point process defined on the surface of the Earth:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-dm5er3
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-h6txtp
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-c96vjb
Scope (2)Survey of the scope of standard use cases
Generate two realizations from a Diggle–Gates point process:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-pjmeyf
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-y8f38b
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-kv2ge2
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-casa32
Generate two realizations from a Diggle–Gates point process on the surface of the Earth:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-omonh
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-ccigf0
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-2efjv
Visualize the point configurations:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-nozzkz
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-e4zptm
Options (3)Common values & functionality for each option
Method (3)
Use the Markov chain Monte Carlo simulation method:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-mr431h
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-q096j
Specify the number of recursive calls to the sampler:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-b28ma3
Specify the length of the run:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-hxjlyn
Provide an initial state for the simulation:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-gx4n0o
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-ca6pqg
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-elpsh
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-kkjl0b
Visualize the points in the sample:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-scg73
Possible Issues (1)Common pitfalls and unexpected behavior
By default, the simulation will run until the number of points converges to a steady state, or until the default number of iterations is reached:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-hrgsq5
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-qppghp
Raise the number of recursive calls to the sampler:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-zur8bp
Specify a larger length of run:
https://wolfram.com/xid/0fojh6vloa9efnb3ueq-7fvnc4
Wolfram Research (2020), DiggleGatesPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.Text
Wolfram Research (2020), DiggleGatesPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.
Wolfram Research (2020), DiggleGatesPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.CMS
Wolfram Language. 2020. "DiggleGatesPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.
Wolfram Language. 2020. "DiggleGatesPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.APA
Wolfram Language. (2020). DiggleGatesPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html
Wolfram Language. (2020). DiggleGatesPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.htmlBibTeX
@misc{reference.wolfram_2025_digglegatespointprocess, author="Wolfram Research", title="{DiggleGatesPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html}", note=[Accessed: 27-March-2025
]}BibLaTeX
@online{reference.wolfram_2025_digglegatespointprocess, organization={Wolfram Research}, title={DiggleGatesPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html}, note=[Accessed: 27-March-2025
]}