DiggleGatesPointProcess
DiggleGatesPointProcess[μ,ρ,d]
![]() 内の一定の強度 μ と相互作用半径 ρ のDiggle–Gates点過程を表す.
内の一定の強度 μ と相互作用半径 ρ のDiggle–Gates点過程を表す.
詳細


- DiggleGatesPointProcessは,点が互いに半径 ρ 以内の点についてソフトコア減少反発対相互作用を持ちそれ以外は一様分布に従う点配置をモデル化する.
-
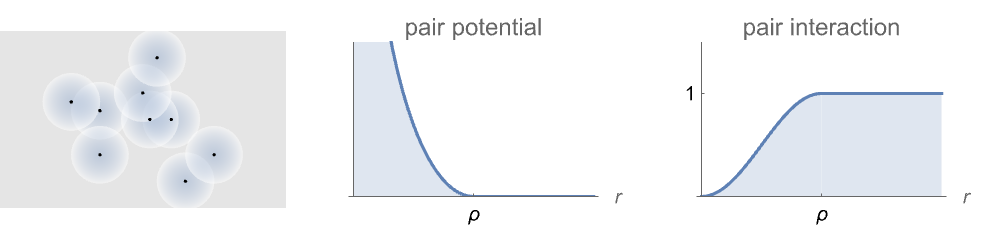
- Diggle–Gates点過程は,その強度 μ とどちらも以下のように ρ によってパラメータ化可能な対ポテンシャル
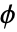 あるいは対相互作用
あるいは対相互作用 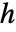 についてGibbsPointProcessとして定義することができる.
についてGibbsPointProcessとして定義することができる. -
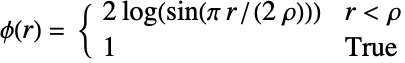
対ポテンシャル 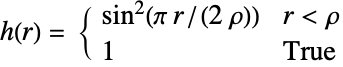
対相互作用 - 観測領域 reg におけるDiggle–Gates点過程DiggleGatesPointProcess[μ,ρ,d]からの点配置
 は,PoissonPointProcess[1,d]について
は,PoissonPointProcess[1,d]について ![mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]) mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])](Files/DiggleGatesPointProcess.ja/8.png) に比例する密度関数
に比例する密度関数 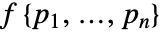 wも持つ.
wも持つ. - 点
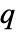 を点配置
を点配置 に追加する際のPapangelouの条件付き密度
に追加する際のPapangelouの条件付き密度 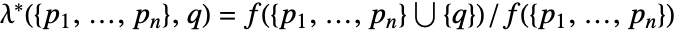 は
は ![mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm]) mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])](Files/DiggleGatesPointProcess.ja/13.png) である.
である. - DiggleGatesPointProcessでは,μ と ρ は任意の正の数でよく,d は任意の正の整数でよい.
- DiggleGatesPointProcessはGibbsPointProcessの特殊ケースである.
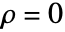 のとき,DiggleGatesPointProcessは簡約されてPoissonPointProcessになる.
のとき,DiggleGatesPointProcessは簡約されてPoissonPointProcessになる.- 次は,StraussPointProcessについてのRandomPointConfigurationにおける可能なMethod設定である.
-
"MCMC" マルコフ(Markov)鎖モンテカルロ法における出生死滅過程 "Exact" 過去からのカップリング法 - 次は,EstimatedPointProcessにおけるDiggleGatesPointProcessについてのPointProcessEstimatorの可能な設定である.
-
Automatic パラメータ推定器を自動選択する "MaximumPseudoLikelihood" 擬似尤度を最大にする - DiggleGatesPointProcessは,RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる.
例題
すべて開くすべて閉じるスコープ (2)
オプション (3)
Wolfram Research (2020), DiggleGatesPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.
テキスト
Wolfram Research (2020), DiggleGatesPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.
CMS
Wolfram Language. 2020. "DiggleGatesPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html.
APA
Wolfram Language. (2020). DiggleGatesPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiggleGatesPointProcess.html