DiggleGrattonPointProcess
DiggleGrattonPointProcess[μ,κ,δ,ρ,d]
![]() 上で,一定の強度 μ,相互作用パラメータ κ,ハードコア半径 δ,相互作用半径 ρ を持つDiggle–Gratton点過程を表す.
上で,一定の強度 μ,相互作用パラメータ κ,ハードコア半径 δ,相互作用半径 ρ を持つDiggle–Gratton点過程を表す.
詳細


- DiggleGrattonPointProcessはハードコアDiggle過程としても知られている.
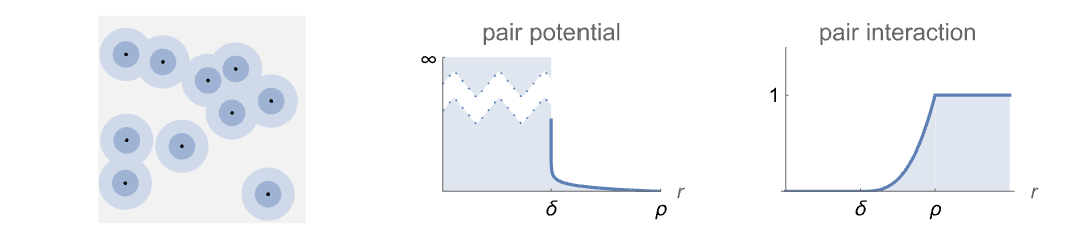
- DiggleGrattonPointProcessは,互いに半径 δ 内にあってはならず,互いに半径 δ と ρ の間にある点について減少反発対相互作用を持つが,それ以外は一様分布に従う点をモデル化する.
- Diggle–Gratton点過程は,強度 μ と,どちらも κ,δ,ρ によって以下のようにパラメータ化される対ポテンシャル
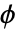 または対相互作用
または対相互作用 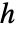 によってGibbsPointProcessとして定義できる.
によってGibbsPointProcessとして定義できる. -
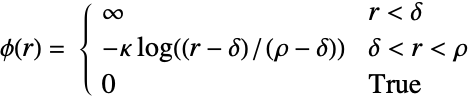
対ポテンシャル 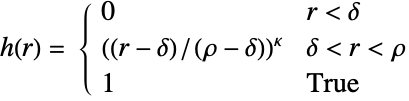
対相互作用 - 観測領域 reg 中のDiggle–Gratton点過程DiggleGrattonPointProcess[μ,κ,δ,ρ,d]からの点配置
 は,PoissonPointProcess[1,d]について
は,PoissonPointProcess[1,d]について ![mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]) mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])](Files/DiggleGrattonPointProcess.ja/8.png) に比例する密度関数
に比例する密度関数 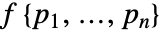 を持つ.
を持つ. - 点 q を点配置
 に加える際のPapangelou条件密度
に加える際のPapangelou条件密度 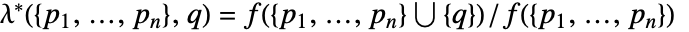 は
は ![mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm]) mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])](Files/DiggleGrattonPointProcess.ja/12.png) である.
である. - DiggleGrattonPointProcessでは,μ,κ,δ,ρ は
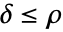 となるような正の数でよく,d は任意の正の整数でよい.
となるような正の数でよく,d は任意の正の整数でよい. - DiggleGrattonPointProcessは
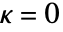 のときは簡約されてHardcorePointProcessになり,
のときは簡約されてHardcorePointProcessになり,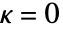 かつ
かつ 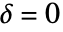 のときはPoissonPointProcessになる.
のときはPoissonPointProcessになる.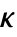 の値が大きくなると過程は半径 ρ 内でより反発的になる.
の値が大きくなると過程は半径 ρ 内でより反発的になる. - 次は,RandomPointConfigurationのDiggleGrattonPointProcessについての可能なMethod設定である.
-
"MCMC" マルコフ(Markov)鎖モンテカルロ方における出生死滅過程 "Exact" 過去からのカップリング法 - 次は,EstimatedPointProcess内のDiggleGrattonPointProcessについてのPointProcessEstimatorの可能な設定である.
-
Automatic パラメータ推定器を自動選択する "MaximumPseudoLikelihood" 擬似尤度を最大にする - DiggleGrattonPointProcessはRipleyKやRandomPointConfiguration等の関数と一緒に使うことができる.
例題
すべて開くすべて閉じるスコープ (2)
オプション (3)
Wolfram Research (2020), DiggleGrattonPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiggleGrattonPointProcess.html.
テキスト
Wolfram Research (2020), DiggleGrattonPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiggleGrattonPointProcess.html.
CMS
Wolfram Language. 2020. "DiggleGrattonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiggleGrattonPointProcess.html.
APA
Wolfram Language. (2020). DiggleGrattonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiggleGrattonPointProcess.html